-
 kasajimajima
kasajimajima
- 295208
- 750
- 373
- 977
???
「手を使って計算している」?
 ざく
@MokeNekox2
ざく
@MokeNekox2
あー、なるほど。 両手の指は10本だから、13から3引くと、10になる。そこから2引いて、片手が3、片手が5。で、5の方からから4引いて1になって、3と1足して4 こうやったのか
2016-10-13 23:57:04
このツイートは権利者によって削除されています。
寄せられた解答たち
 いぬころ
@steraum
いぬころ
@steraum
@Potatsun_643 13-9 =(13-3)-(9-3) =10-6 =(5+5)-(2+4) =(5-2)+(5-4) =3+1 =4
2016-10-13 21:43:01 松本青空: 科学系ITエンジニア
@kalfes
松本青空: 科学系ITエンジニア
@kalfes
@Potatsun_643 とりあえず13から3引いて10の塊作ろうと思ったけどまだまだ五本の指で数えられない数字で引かなきゃならんから元に戻して10-3からさらに2だけ引いて5の塊を作った その5から残りの引く数4引いて1、引かれる数の一の位を足して答えは4 うん、こじつけ
2016-10-13 21:44:29 KAJIWARA Osamu
@kajimoe
KAJIWARA Osamu
@kajimoe
@Potatsun_643 この児童の算術logicでは 5で1バイトと予想します! pic.twitter.com/GiBsi72HVa
2016-10-13 22:15:22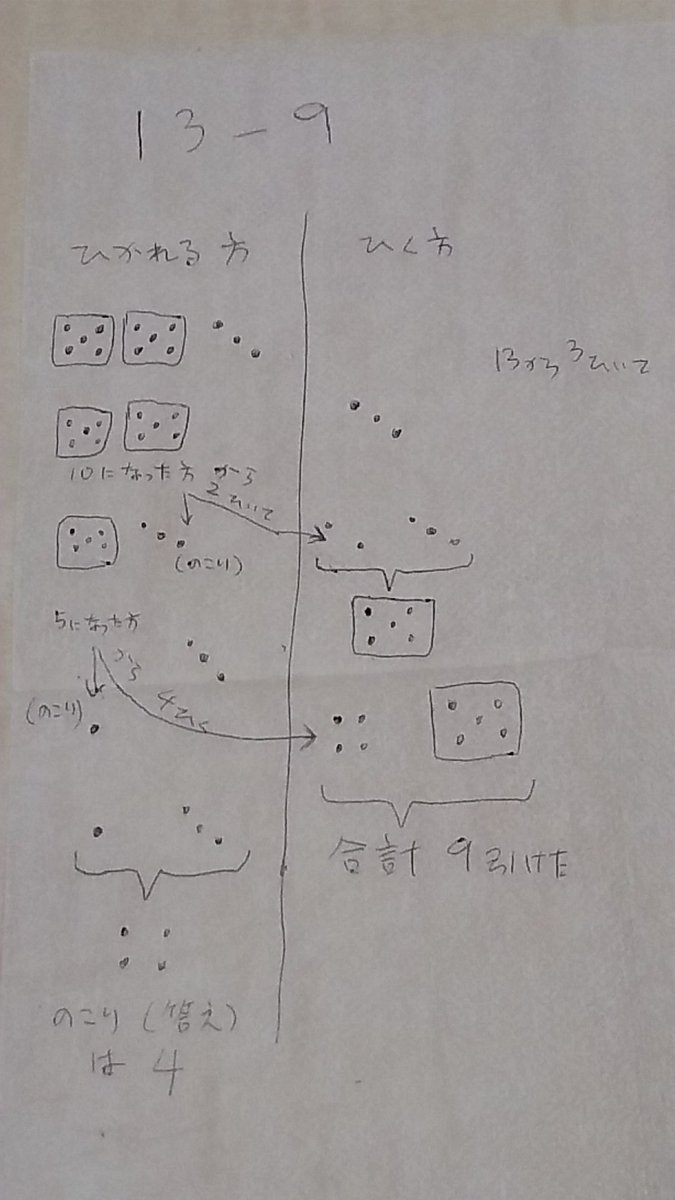 拡大
拡大
