
素数大富豪Advent Calendar12/16 素数大富豪のペアについて
 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
#素数大富豪 Advent Calendar 2016 12月16日【大富豪におけるペア(2枚組)について】 ジョーカー込みのトランプ54枚から7枚(素数大富豪の初期手札)を引いて被りがない確率は約15.9%。6回に5回はペアがあるんですね。これを利用する方法を考えてみました。
2016-12-15 22:29:40 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
ここで素数大富豪におけるペアを話す上で、というか並べ替えて数字を作る上で欠かせないのが3で割ったときの余りです。 例えば169を並べ替えた数(196,619,691,916,961)は全て3で割ると1余ります。これは各位の和がその数を3で割った余りに等しいからです。
2016-12-15 22:51:41 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
証明は字数の関係で避けますが、ここで重要なのがあと1枚何かがくれば3の倍数になってしまう数があるということです。 例えば49を持っていて1枚引いたら2が来て(3枚出しでは)3の倍数しか作れない!ということが起きます。これは2に限ったことではなくn≡2 (mod3)なら起きますね。
2016-12-15 22:58:46 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
つまり「受け入れ可能」な数というのが必ず限られるということです。もちろんこれはペアにも言えます。そこで受け入れ不可能な数(3の倍数になってしまう数)を表にまとめてみました。逆に言えばこれ以外の数が来れば素数になる可能性がある(最悪でも3の倍数にはならない)ということですね。 pic.twitter.com/Ia6UrewVWY
2016-12-15 23:07:33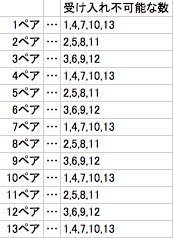 拡大
拡大
 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
そこで私は少し考えました。本当に受け入れ不可能な数は3の倍数関係だけなのかと。そしてペア限定においてそれ以外の数があることに気付きました。それは「11」の存在です。
2016-12-15 23:10:21 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
しかしこれは1桁のペアに限った話なので一般性にはかけるんですけどねw。 例えばNN(Nは1~9)が手札にあり、11を引いてきました。この3枚を組み合わせてみましょう。 NN11→N01×11 N11N→(N×91+10)×11 11NN→10N×11 全部11の倍数になりました。
2016-12-15 23:16:42 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
これは1001が11の倍数(1001は7×11×13の連続3素数の積で表せる楔数ですね)だから起きる現象です。 これをふまえて受け入れ不可能な数とペアを表にしてみましょう。こんな感じになりました。 pic.twitter.com/nKYIHixxn2
2016-12-15 23:25:54 拡大
拡大
 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
さていよいよ本題、ペアとどの数を組み合わせれば素数になるかです。 まずは偶数から。偶数が1の位になると必ず合成数になるので1の位に来る数は自ずと限られます。え?5が偶数に入ってる?5は素数大富豪では偶数でしょ? 参考動画: nicovideo.jp/watch/sm298112… pic.twitter.com/r5X6Mn0MB7
2016-12-15 23:32:12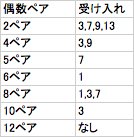 拡大
拡大
 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
奇数は順序を入れ替えられるため、受け入れが広いですねー。つまり奇数のペアを持ってるときは3枚出ししやすいということです。まぁ迷ったらキングサンドしてみたり(13で挟む)、~77を後ろに付ければ大体素数になるでしょう。(てきとー) pic.twitter.com/uJlp0Q6wC1
2016-12-15 23:54:23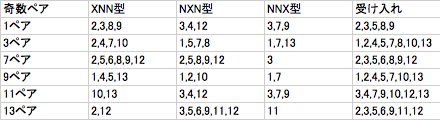 拡大
拡大
 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
これをふまえて先ほどの表に受け入れ可能な数字を入れてみました。特筆すべきは3ペアと7ペアですね。受け入れられる数字は全て素数にすることが出来ます。次いで9ペアと13ペアが8以外で素数が作れます。 pic.twitter.com/cYu8qeAFdq
2016-12-16 00:01:19 拡大
拡大
 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
そろそろまとめを。 他人から手札に干渉しないタイプのゲームでは、手札を見やすくするために並べ替えると思います。代表的なのが麻雀の理牌でしょう。トランプも無意識にペアを作って並べる人も多いのではないでしょうか。そんなときにこのペアについて知っていれば簡単に3枚出しが出来ますね。
2016-12-16 00:09:10 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
あと覚えやすいのがペアを使う素数の特徴です。案外2種類の数で出来た数は印象に残りやすく、3種類になると覚えにくくなるものです。 例えば何かしらのスポーツの結果が33-4なら覚えやすいですが、52-9なら印象に残りにくそうでしょう?これを「23^2だ!美しい!」と思った人は末期です
2016-12-16 00:14:28 ゆぅくりっど
@akatanana
ゆぅくりっど
@akatanana
さて明日17日は @ldsynEin2357 さんの素数大富豪を通して得たものについてです。2357で思い出しましたが、素数が並んだ数としてコープランド-エルデシュ定数は有名ですが、スマランダンク-ウェリン数はあまり知られてないですね。気になった方は調べてみてはいかがでしょうか?
2016-12-16 00:30:36