３の３　ローレンツ収縮とローレンツ膨張も時計がいっぱい。

ローレンツ変換のローレンツ氏が、しでかしたケアレスミスを説明する前に、「1887年に行われたMichelson-Morleyの実験」解釈に不備があることを、指摘しておく。数学の世界なら構わないが、電磁現象世界で、円とか正方形を見るということは、懐中電灯で円錐底面を造ること。

2017-03-17 03:31:40

zionadchat @zionadchat

円とか正方形の有限範囲を構成する各点の状態情報を知ることは、ミンコフスキー過去円錐底面の状態を知るようなものである。このことについてのトリック説明は、いまは飛ばして、「1887年に行われたMichelson-Morleyの実験」解釈の不備にわずかに触れながら、指摘検証を終わらす。

2017-03-17 03:45:08

zionadchat @zionadchat

「1887年に行われたMichelson-Morleyの実験」参考は、ここで。 1.3 Michelson-Morleyの実験（絶対空間・Etherの概念の破棄から相対的な空間へ） jsimplicity.com/ja_Report_Rela… pic.twitter.com/rUR9WMKoOr

2017-03-17 03:36:50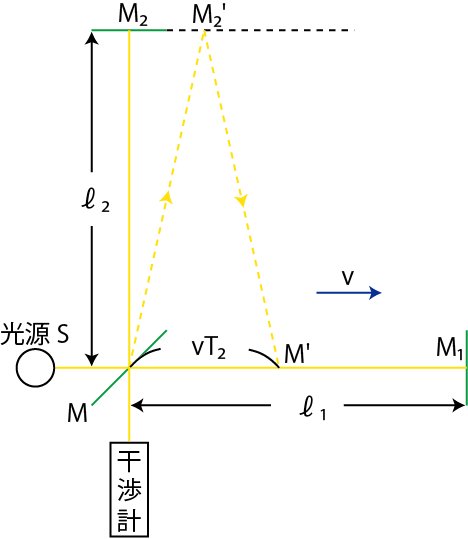

拡大

zoutchatjp @zoutchatjp

ローレンツ変換は単位円を描いて、斜辺緑色が光速。速度0のときは黄色が、長さ1。速度1。つまり光速になったときが長さ0になる。これがローレンツ変換。いきなり説明なしでこの図を見せてもなんだかわからんと思うが、 pic.twitter.com/JXlLYeGlSK

2017-03-17 03:51:39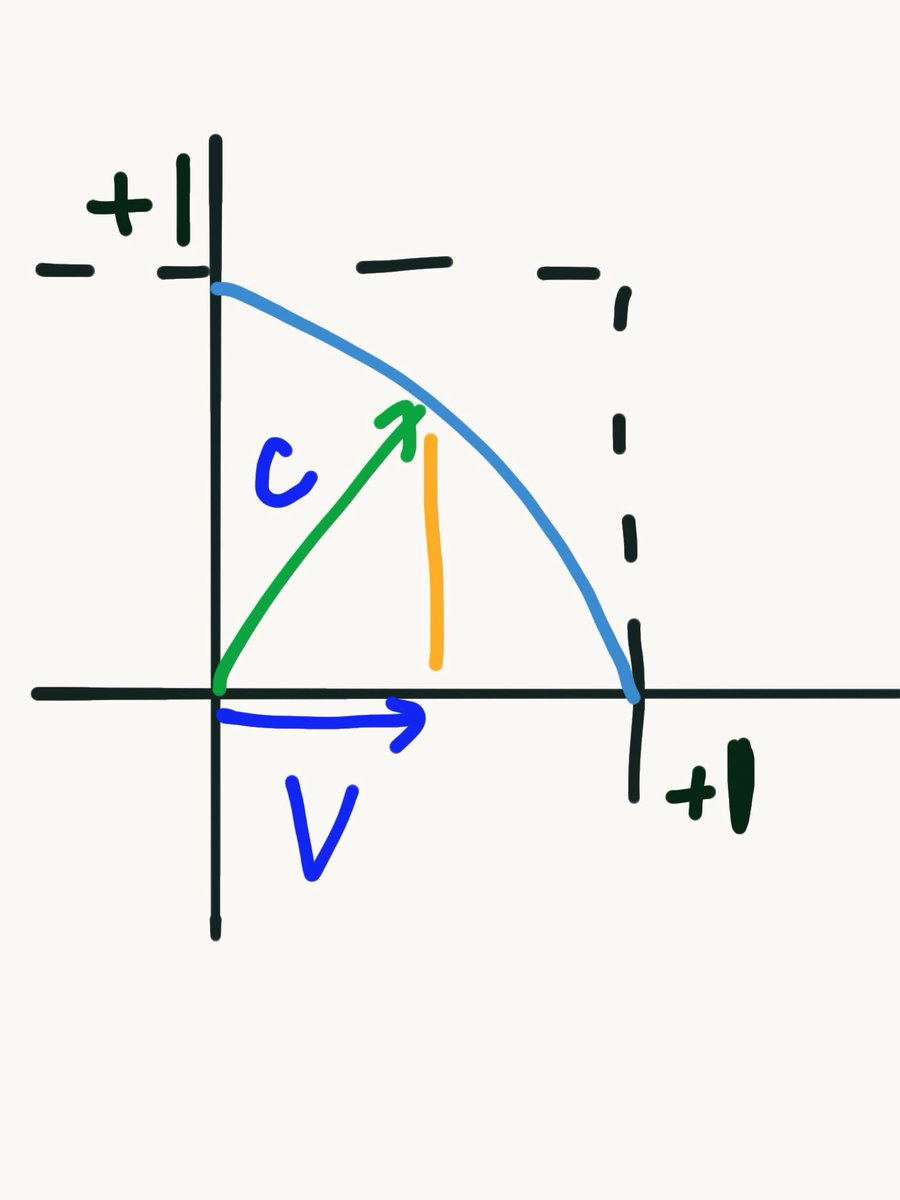

拡大

zionadchat @zionadchat

"J Simplicity（ジェイシンプリシティ）" は理論物理学のサイト jsimplicity.com/ja_Report_Rela… では、速度によって斜辺の長さが変わる。マイケルソン＆モーリーの実験で。これを斜辺の長さ一定。たとえば１秒間にしたものが、俺の図。 pic.twitter.com/2iimkuoUsQ

2017-03-17 03:55:55

拡大

zionadchat @zionadchat

俺の出した図は、ハーフミラーを通過した光子が、進行方向ではない、方向・へ、向かった光子が１秒で鏡にぶつかり、１秒でハーフミラーに戻ることで、干渉を検出する感じになってる。斜辺の長さ一定にして、マイケルソン＆モーリーの実験を描き直すと、ローレンツ変換は、斜辺を黄色縦線に短縮すること

2017-03-17 04:01:00

zoutchatjp @zoutchatjp

ローレンツ収縮、ローレンツ短縮は、緑色斜線を黄色縦線に変換することで、マイケルソン&モーリーの実験で、エーテルの影響がないを説明しようとしただけ。この解釈には、数学幾何空間の古典物理学のものであり、瞬時に情報収集ができん電磁現象世界の物理空間の実状を無視している。 pic.twitter.com/OzLvYKgJml

2017-03-17 04:15:59

拡大

zoutchatjp @zoutchatjp

ローレンツ収縮ローレンツ短縮 keisan.casio.jp/exec/system/11…

2017-03-17 04:16:58

zionadchat @zionadchat

エーテルの影響を察知しようとした、マイケルソン＆モーリーの実験から、ローレンツ収縮を求めたので、ローレンツ膨張を忘れたのが、１９世紀生まれの方々の敗因。

2017-03-17 04:24:28

zionadchat @zionadchat

エーテルの存在確認に、干渉を使うことができないんだが、電磁現象世界の三角測量手続き知らない１９世紀の方々は、それ知らずに、マイケルソン＆モーリーの実験解釈から、動いている物体は縮むと解釈してしまった。理由は、くだらん単純トリックが公知になったとき、わかるんで、いまは飛ばす。

2017-03-17 04:28:21

zionadchat @zionadchat

かなり乱暴な書き方したが、こっからが本番。ガリレオ相対性原理で考える。電磁現象世界の空間は、従来の数学が想定していた空間イメージと異なるものになるんで、それをいきなり見せびらかしても通用しない。ので、まずはガリレオ相対性原理を手がかりにする。

2017-03-17 04:31:54

zoutchatjp @zoutchatjp

長さ2の線分客車が、光速の10倍で移動したら、客車中央位置を基準に、数直線に、こんな風に描くことになる。物理知見により、線路に対して光速を超える列車を描いても意味ないので、速度0から速度1(光速C)の範囲で描くことにする。 pic.twitter.com/MTw5nIT1K0

2017-03-05 14:04:19

拡大

zoutchatjp @zoutchatjp

遠近法なら、手前の客車を大きく描き、奥の客車を小さく描く。絵画は、物理空間でないので、奥に描かれたものも、手前に描かれたものも、瞬時に状態把握をできるとする。数学座標空間を数学者が瞬時に超越的に把握するように。電磁現象世界の物理空間じゃ、無理だけどね。 pic.twitter.com/330B0i0Jo9

2017-03-17 04:47:58

拡大

zoutchatjp @zoutchatjp

同じ大きさ、全長の客車中央から左右に光子が動く。これを光速で燃え拡がる客車床導火線に見立てる。客車は動いていない。光速はどれも一定速度だけど、遠近法で描かれた絵画を動画にすると、手前と奥じゃ、光子の「見かけ」速度が異なる。これは物理の問題じゃなく、表記によるもの。 pic.twitter.com/EK0FhloNWW

2017-03-17 05:02:03

拡大

zoutchatjp @zoutchatjp

客車速度をVとして、等速直線運動とする。客車の静止時の長さを2として、客車速度を光速、光速10倍、光速100倍として、黒板やノートの上に同じ長さで描くと、こんな感じ。単位だけ換える。地図の縮尺と同じ感じ。パソコン画面の大きさ変わらないけど、縮尺で、見える範囲変わる。 pic.twitter.com/wpZFMkLorv

2017-03-17 05:07:51

拡大

zoutchatjp @zoutchatjp

このとき、それぞれの縮尺度合いの違う数直線に、定義から、1秒前と1秒後の線分客車中央位置を描いたんで、今度は線分客車長さ2を描こう。そうすると、縮尺度合い違いの数直線に合わせて、線分客車の「見かけ」長さを、それぞれの数直線刻み間隔に比例させて描く。 pic.twitter.com/394NX1Ak1V

2017-03-17 05:11:34

拡大

zionadchat @zionadchat

片対数グラフ（かたたいすうぐらふ、semilog graph）だと、１秒前や１秒後の線分客車中央位置をキチッとプロットできるけど、線分客車長さの「見かけ」が、速度毎にバラバラになる感じ。 google.co.jp/search?q=%E7%8… pic.twitter.com/gtRn6sx5IH

2017-03-17 05:18:12

拡大

zionadchat @zionadchat

懐中電灯で円錐形で、線分２区間を照らし出すのと、２ｘ２の正方形を収めて照らし出すのとでは、円錐形、視野角が同じなら、壁面や床面から、点光源の位置を違う距離で離さなきゃと同じ。正方形の対角線は２√２になるから。ミンコフスキー空間で連想すると、過去度合いが違う。

2017-03-17 05:21:21

zionadchat @zionadchat

ま、そういう細々したことは、後で説明することにして、

2017-03-17 05:22:45

zoutchatjp @zoutchatjp

停まっている客車の中のヒトが、客車中央で光を放ったら、1秒後に客車端に光子が到着する。 pic.twitter.com/iJZkf5jtSU

2017-03-17 05:34:21

拡大

zoutchatjp @zoutchatjp

ちょっと図が見にくいが、右に等速直線運動している場合。ガリレオ相対性原理で描くと、客車長さは保存されるけど、１秒間に光子が客車右端に到着す長さが長くなってる。速度が、光速超えた感じに表記されてる。だから縮むんだと、短絡しちゃったのが、19世紀生まれの方々。 pic.twitter.com/LYaYZW4EXN

2017-03-17 05:47:01

拡大

zoutchatjp @zoutchatjp

客車左端に注目してみよう。ガリレオ相対性原理で移動した客車左端より、左に、左に向かった光子が存在するハズ。同時性破綻の思考実験じゃ、従来は、先に客車後方ぶつかるのが、線路慣性系からだと見えると信じてたんだから。こっちはローレンツ膨張と呼ぶべきじゃないか。ね。 pic.twitter.com/U7Jtev4Usc

2017-03-17 05:53:04