ベン図と素数と三次元
-
Polyhedrondiary
- 26451
- 31
- 2
- 0
-
- いいね！0
きっかけ。「ベン図でソリューション」的なページを見かけました
{3,5/2} 大二十面体
@Polyhedrondiary
ちょっとこの4個のやつを「ベン図」と呼ぶとか，激怒する人多数なのでは…。 Venn Diagrams Solution | ConceptDraw.com conceptdraw.com/news/article.p… pic.twitter.com/2FjrXGIR2z
2017-03-29 22:14:34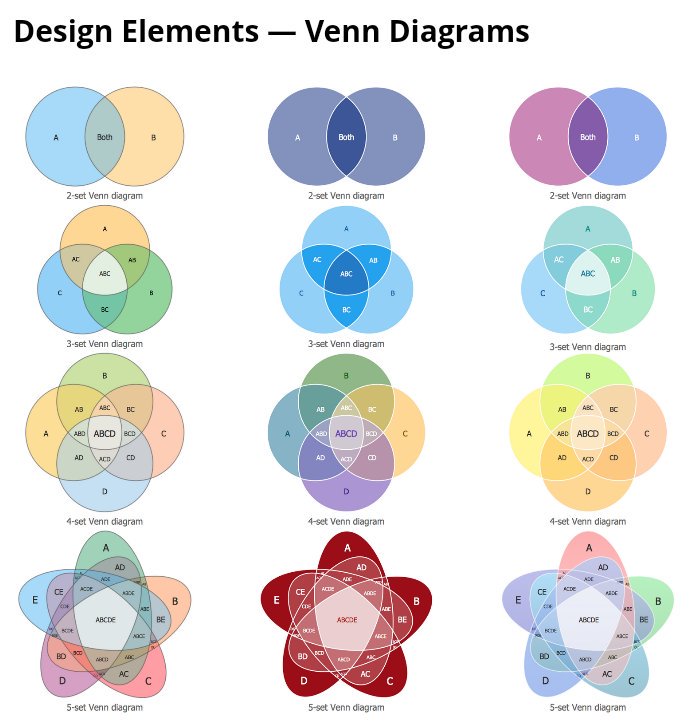
拡大
拡大
{3,5/2} 大二十面体
@Polyhedrondiary
5個のときのベン図は合ってるけど，4個のあれはベン図じゃないよね？ pic.twitter.com/3sBW4p7wGp
2017-03-29 22:18:41
拡大
4は合成数なので，回転対称なベン図は描けません
{3,5/2} 大二十面体
@Polyhedrondiary
4個のときの正しいベン図はこちら。考案者ジョン・ベンはなるべく対称性の高いのを描こうとしたけど，これが精一杯だった。 ベン図が回転対称に描けるのが，素数個のときだけだと判明するのは一世紀も後のこと。 goo.gl/images/Gdp5pI
2017-03-29 22:28:43
MIZUHARA Bun
@bmizuhara
@Polyhedrondiary ご存知かと思いますが、回転対称なベン図が作れるのはNが素数の時に限るらしいですね。ここにN=11の場合の図がありますが、もう何が何やら…。 macalester.edu/smailgallery/p…
2017-03-29 22:45:54
{3,5/2} 大二十面体
@Polyhedrondiary
集合11個の回転対称ベン図，2012年にやっと構築できたっていうのがすごいです Logic blooms with new 11-set Venn diagram google.co.jp/amp/s/www.news… pic.twitter.com/D8HEAOOwp3
2017-03-30 08:13:31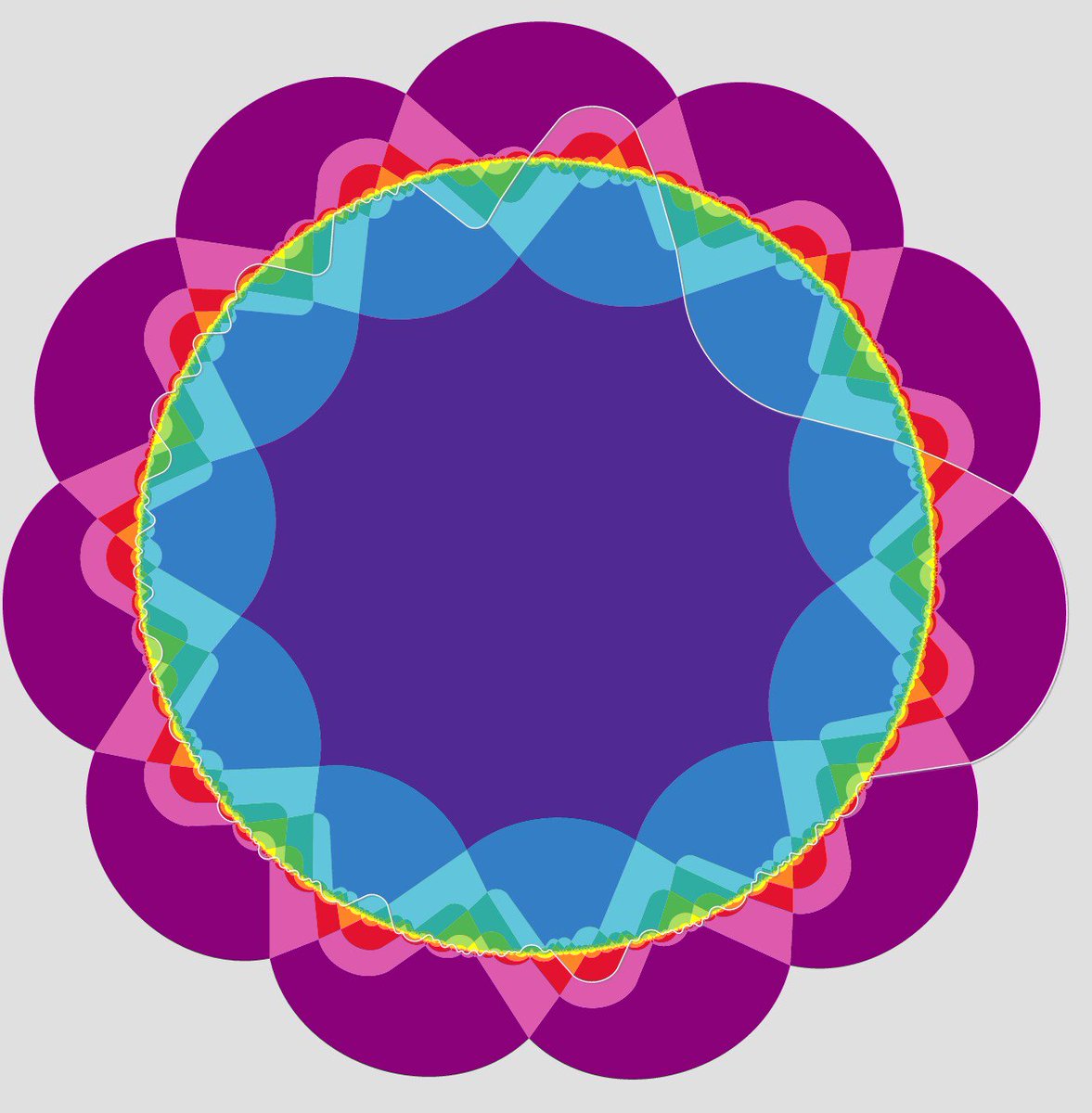
拡大
拡大
みっくん：Cb.Fl.発注済み
@mimicn393983
僕の作った5集合回転対称ベン図も見てくれ。 pic.twitter.com/bHdfOvpyiO
2017-03-30 10:13:38
拡大
みっくん：Cb.Fl.発注済み
@mimicn393983
回転対称ベン図の構築手順は、そこまで複雑ではない。 実際、素数個集合であれば回転対称は存在するし。 めんどくさいにはめんどくさいが。 7集合7角形でベン図を構成しようとしているが、5集合の時ほどにきれいなものがなかなか作れない。
2017-03-30 10:21:33
のだぬき
@pon_qyu_pon
たしか、高校のときに友達に見せてもらった青チャートに載っていた気がする。 四項目のベン図は、こんなに対称的ではなく、凄くいびつな形だった。 twitter.com/Polyhedrondiar…
2017-03-30 10:59:47
MIZUHARA Bun
@bmizuhara
@Polyhedrondiary 先ほど示したサイトに「symmetric Venn diagrams exist for n sets if and only if n is a prime number」とありますから、逆も成り立つみたいです（試そうとは思いませんが ^^;）
2017-03-30 12:45:59
Smoky@「サイバー術 プロに学ぶサイバーセキュリティ」「暗号技術実践活用ガイド」翻訳
@smokyjp
３個より多いベン図なんて考えたことなかった。 twitter.com/polyhedrondiar…
2017-03-30 12:51:43
7931
@wed7931
そもそも「ベン図」の定義って何だっけ…と調べてみた。Wikipediaだけど。 / ベン図 - Wikipedia ja.m.wikipedia.org/wiki/%E3%83%99…
2017-03-30 15:01:34
トミー＞18 Weeks after Fully Vax
@ytommy405
そうなんだ！ベン図ってn個の集合に対して2^n個の領域を持つのが定義なんだ。4個の集合のときの間違った例はよく見るな。
2017-03-31 08:36:14
ロコリン🥚ネコぱらレビュアーズ△小惑星69T🍆🍡
@L0C0P
4個のがなんでベン図じゃないか初見ではわからなかったけどよく見たらACとBDがない。楕円形にして引き延ばせばこの配置でベン図にできた可能性が微レ存? twitter.com/Polyhedrondiar…
2017-03-31 15:32:50
{3,5/2} 大二十面体
@Polyhedrondiary
例えばAを楕円にしてACを作るとBCDが失われてしまったりでうまくいかないのです twitter.com/L0C0P/status/8…
2017-03-31 21:58:21ここで重要な指摘が！
{3,5/2} 大二十面体
@Polyhedrondiary
確かにその「三次元ベン図」なら4集合でも回転対称(どころか四面体対称)なものが描けますね…。その発想はなかった twitter.com/Valquasard/sta…
2017-04-01 21:33:13
{3,5/2} 大二十面体
@Polyhedrondiary
でもベン図を三次元に上げてしまうと，集合の重なり具合がちょっと分かりにくいのが難点。 …いや11集合の二次元ベン図なんかも実用性は皆無だから，そんなのは擬似問題なのかも twitter.com/Polyhedrondiar…
2017-04-01 21:37:47立体的なベン図(ベン立体？)
Geogebraで描いてみました