
ミサイルコマンドが実験装置。 作業3 従来と違う地図技法。戦場で。
-
 zionadchat
zionadchat
- 1080
- 2
- 0
- 0
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
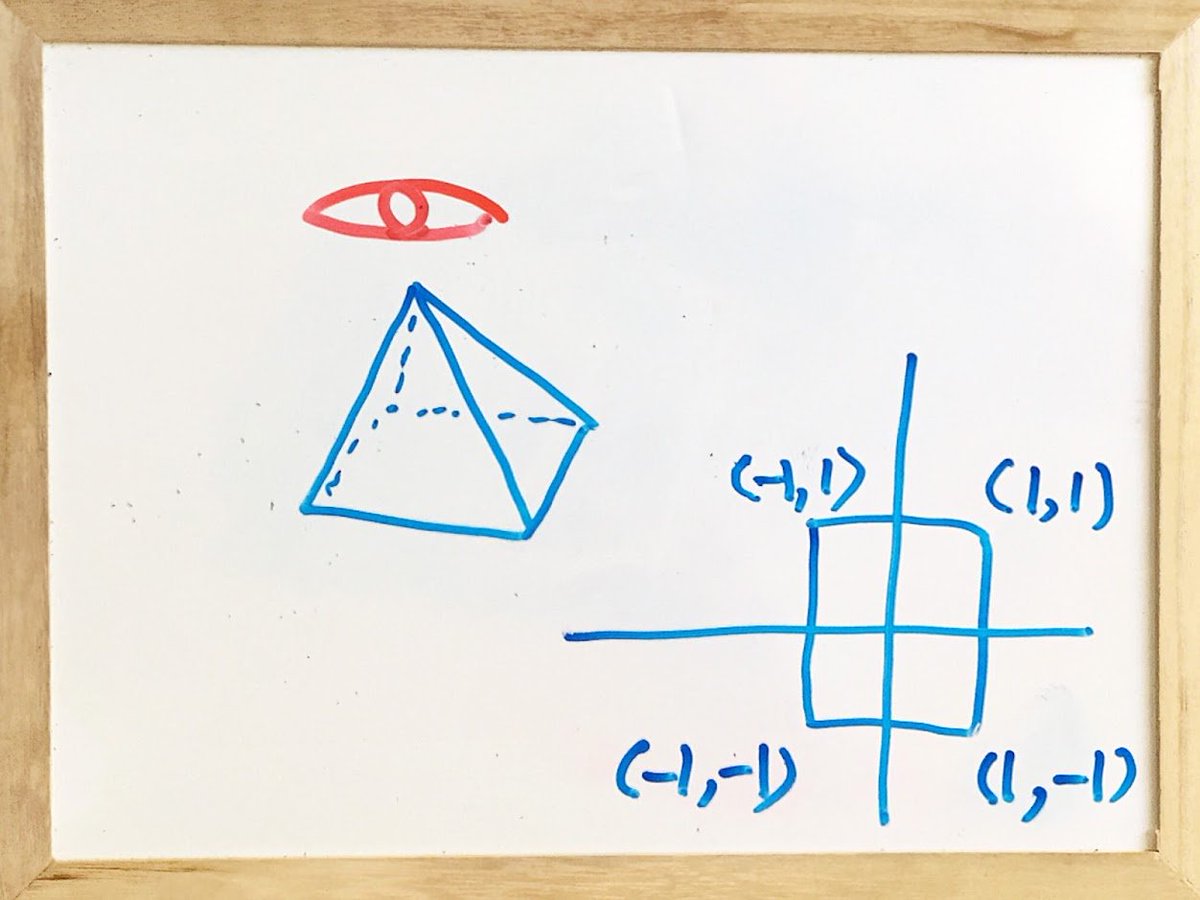
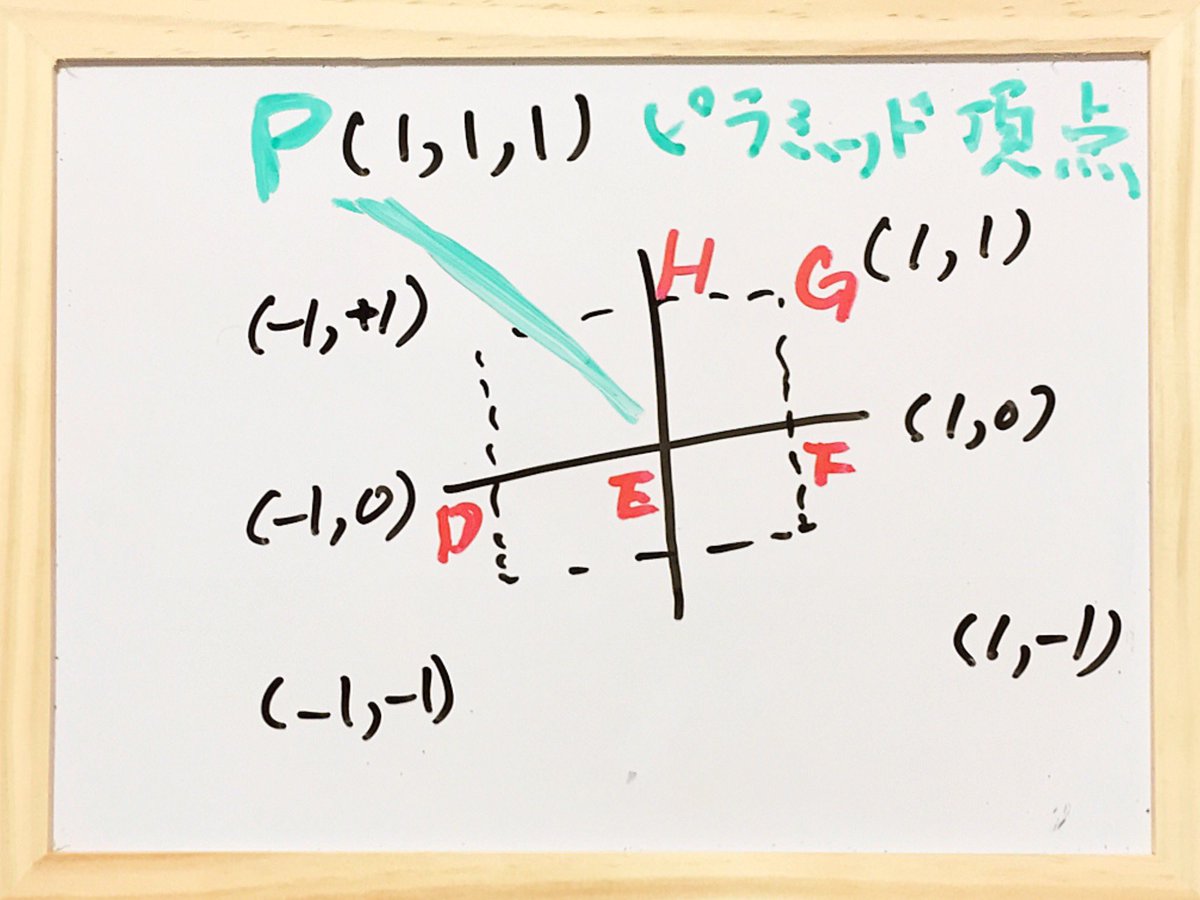
ピラミッド頂点をP。 ピラミッド底面の第1象限部分をEFGH。 ピラミッド底面のx軸線分をDEFとする。 pic.twitter.com/AezZx7qGd2
2017-08-27 02:07:50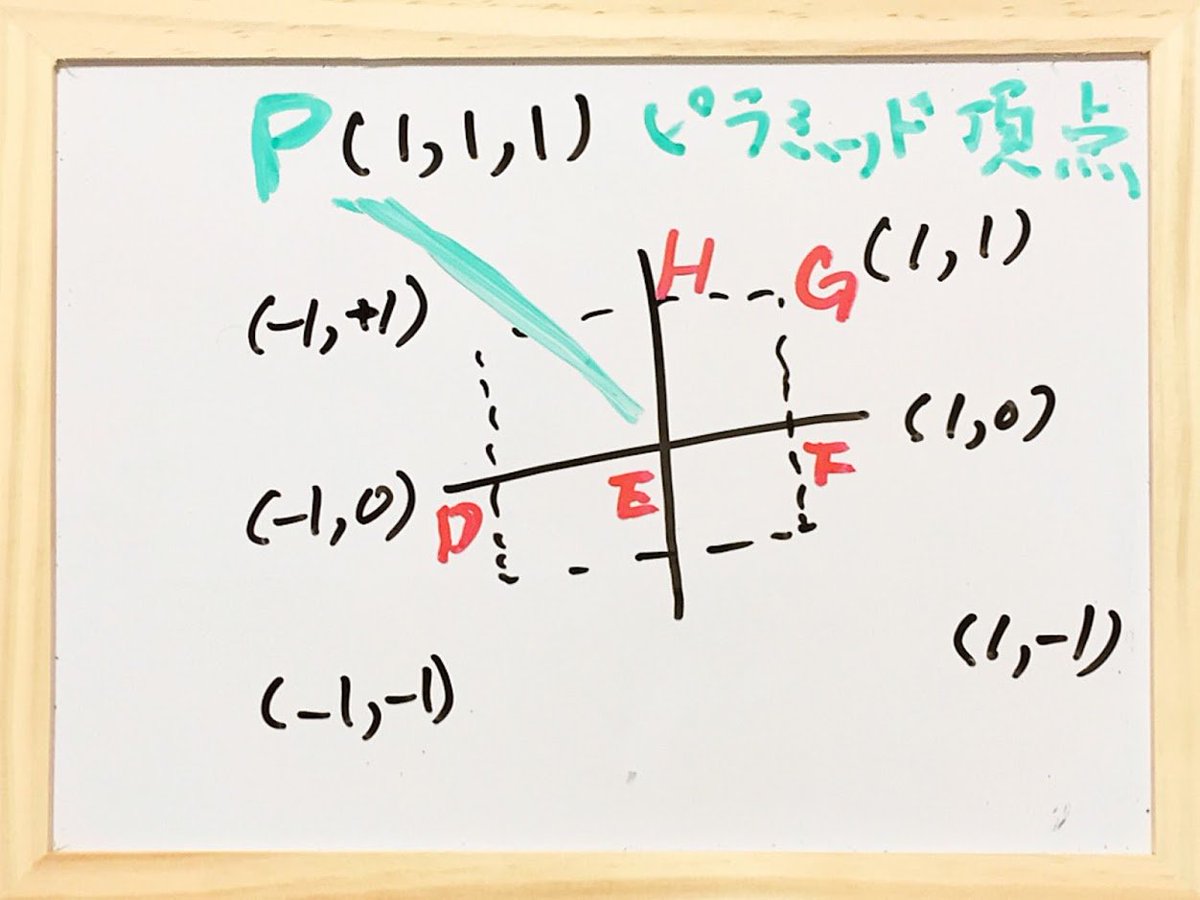 拡大
拡大
 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
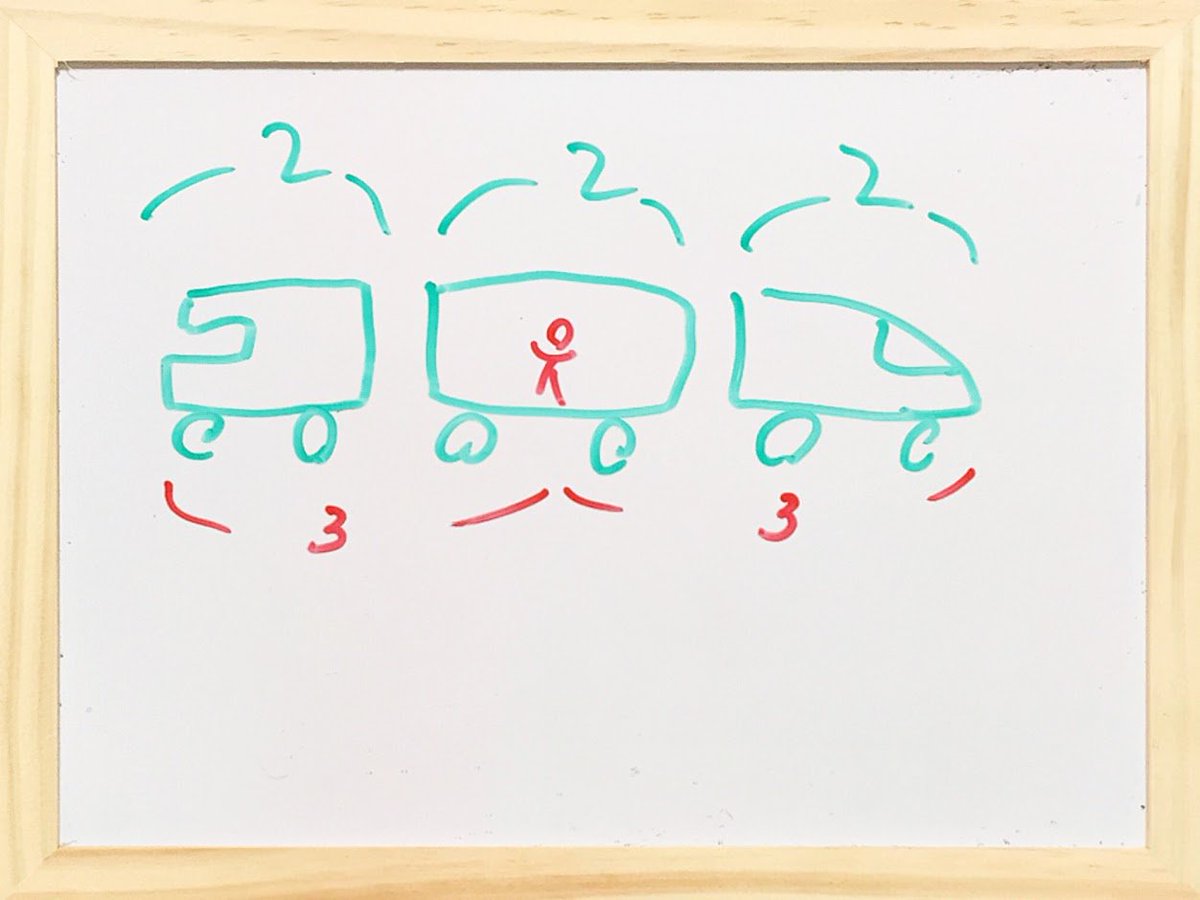
線路を走る客車内で、客車中央で、目を瞑(つむ)る。 展望車・客車・先頭車。それぞれ2光秒長さ。 客車中央から左右に光子ペアを放てば、3秒後に列車両端に到着する。 そう思い込むのが、設計図イメージの世界、想像的座標イメージの世界。 pic.twitter.com/cU8Yaz9CZf
2017-08-27 02:14:00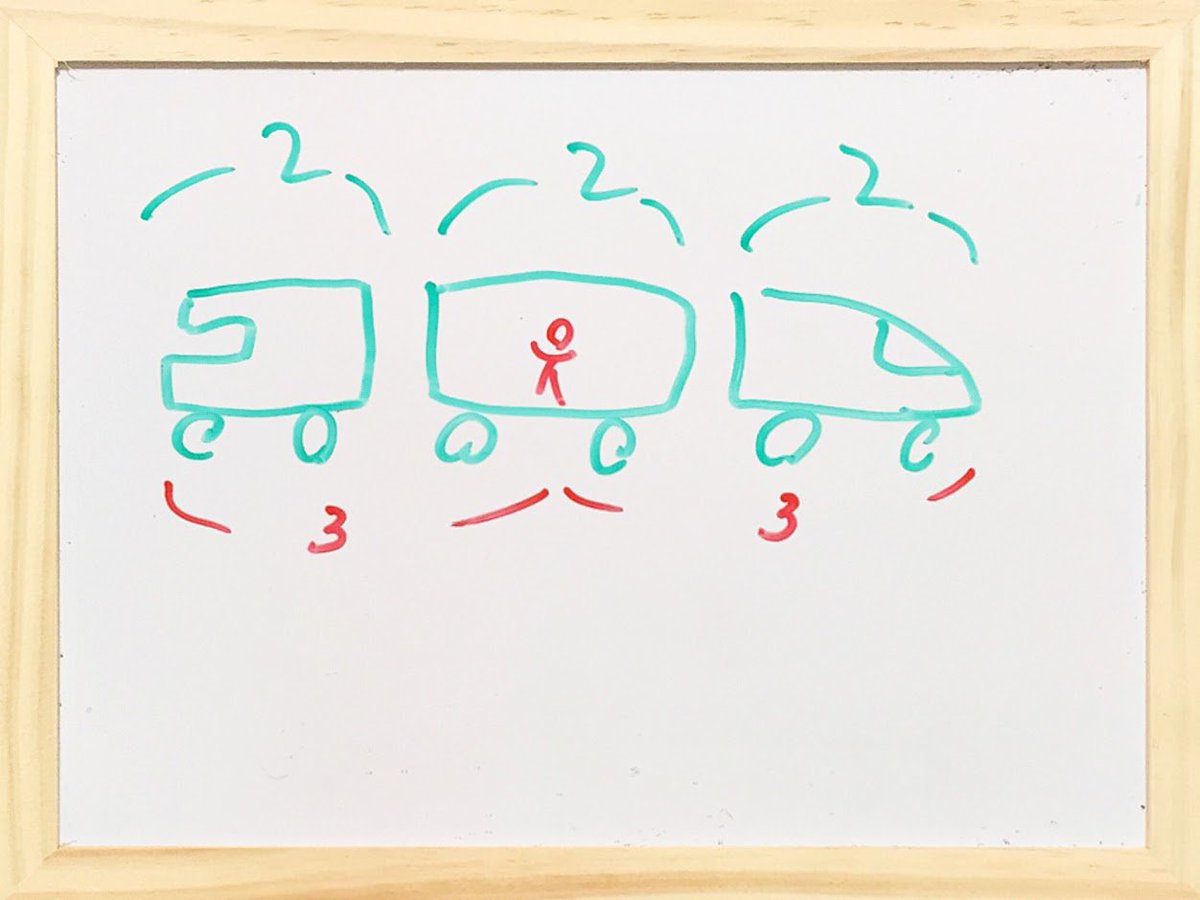 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
線路上の等間隔枕木。1光秒長さ間隔の枕木番号ABC。枕木ABCに埋め込まれた時計が同時にt=0を表示した。 緑人型・赤人型・青人型が同時に右に進み始めた。 pic.twitter.com/OJbPlqRSu4
2017-08-27 02:22:40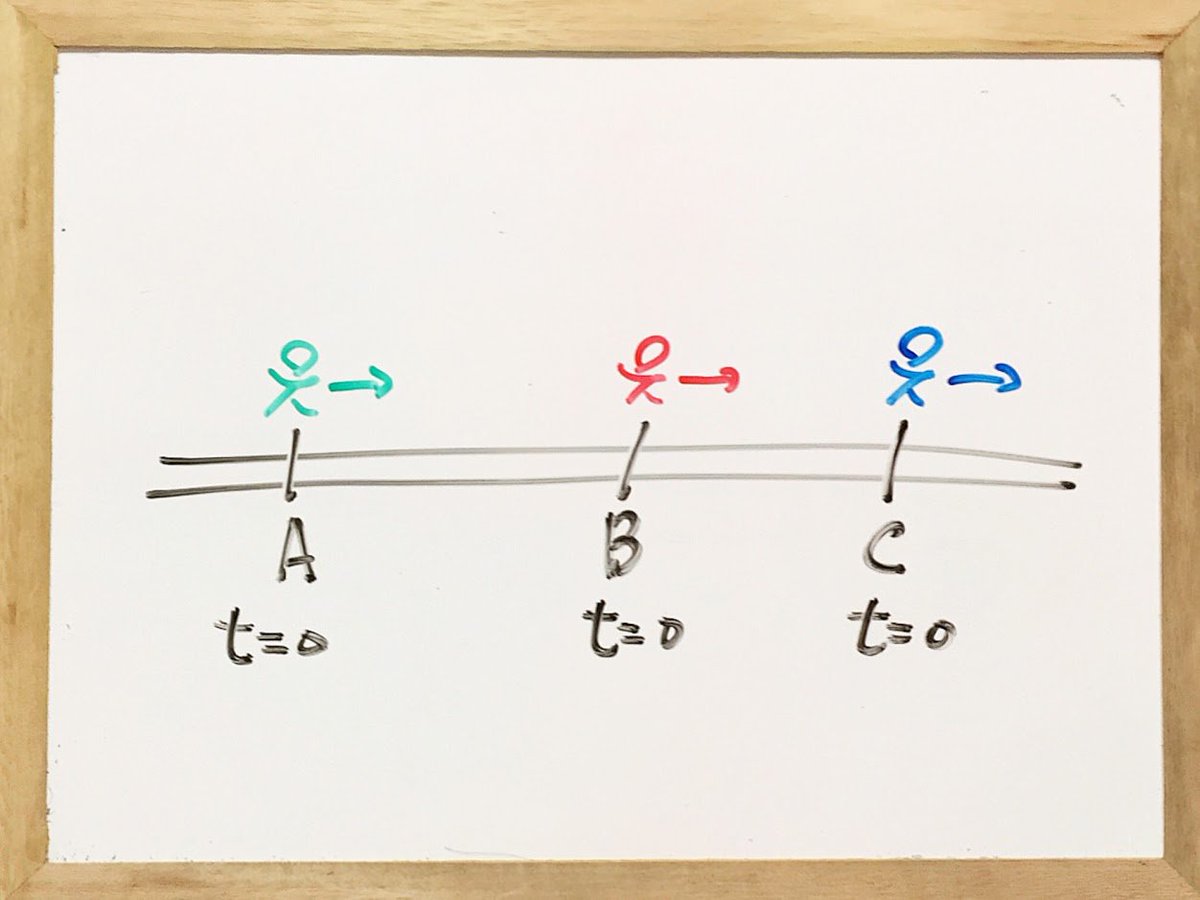 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
停止状態から速度が徐々に上がり、加速が一定になり、速度増加量が徐々に減り、加速が0になり等速直線運動になるまでの横軸(時間t)縦軸(速度V)の図。 緑と赤と青の人型は、停止状態から加速し等速直線運動に入った。 3つの人型も、同じだけ右に進んだ。だから、 pic.twitter.com/PVWn1VyE89
2017-08-27 02:27:00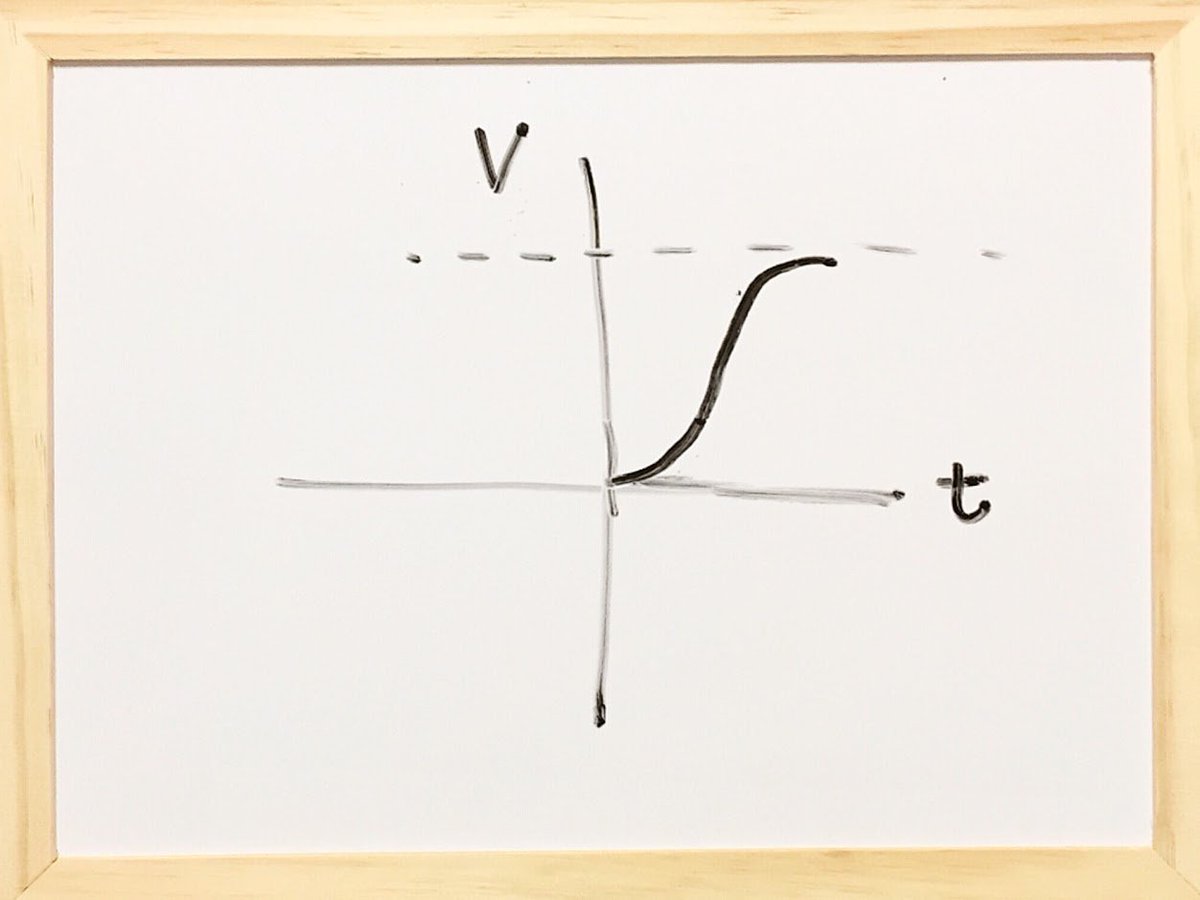 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
3者の位置間隔は、停止時と同じ間隔。 3者をロープで繋げば、先頭は運転手、真ん中は乗客、後尾は車掌。列車と見做せる。 線路を等速直線運動で走っても、直感的に列車は縮まないのが、わかる。
2017-08-27 02:29:48 zionadchat
@zionadchat
zionadchat
@zionadchat
逆に緑人型が1人で線路地点ABCに対して停止状態から動いても等速直線運動状態に入っても、それまでの加速状態での移動距離を含んでも、線路地点ABCそれぞれとの距離は、 緑人型からA地点迄の距離にプラス1したのがB地点。さらにプラス1したのがC地点だから、列車慣性系からも
2017-08-27 02:37:29 zionadchat
@zionadchat
zionadchat
@zionadchat
ローレンツ収縮は、xy平面だけで考えたとき、地球慣性系では、マイケルソンとモーリーの実験装置をE→Hと進んだハズの光子は軌跡が、地球が横ズレして見える宇宙からの慣性系ではE→Jに見えるハズだと思い込んで、 pic.twitter.com/5ldGZWDnTK
2017-08-27 02:42:40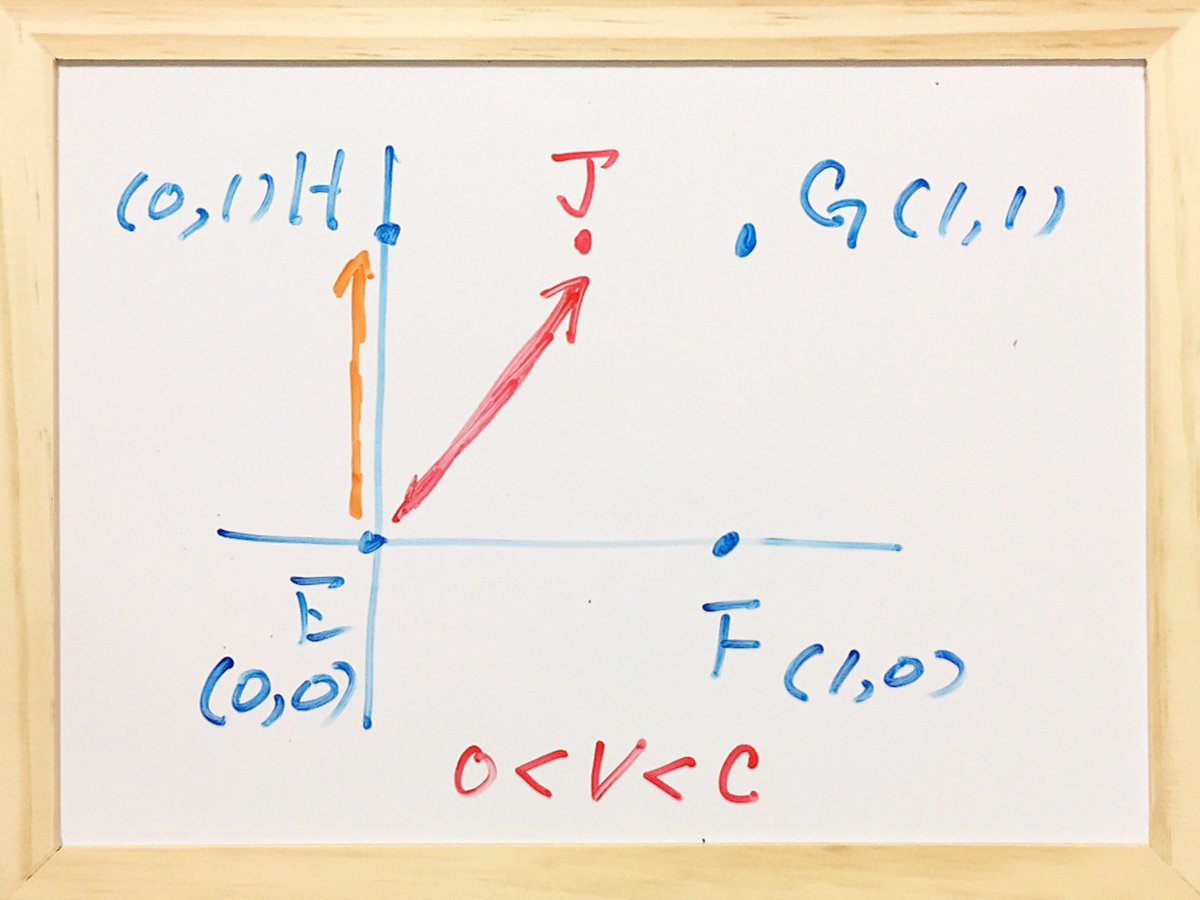 拡大
拡大
 zionadchat
@zionadchat
zionadchat
@zionadchat
オレンジとレッドの線が同じ長さにするには、ローレンツ変換してEJ線分を無理矢理辻褄合わせでEH長さにしただけ。 pic.twitter.com/85xq40ASCx
2017-08-27 02:45:03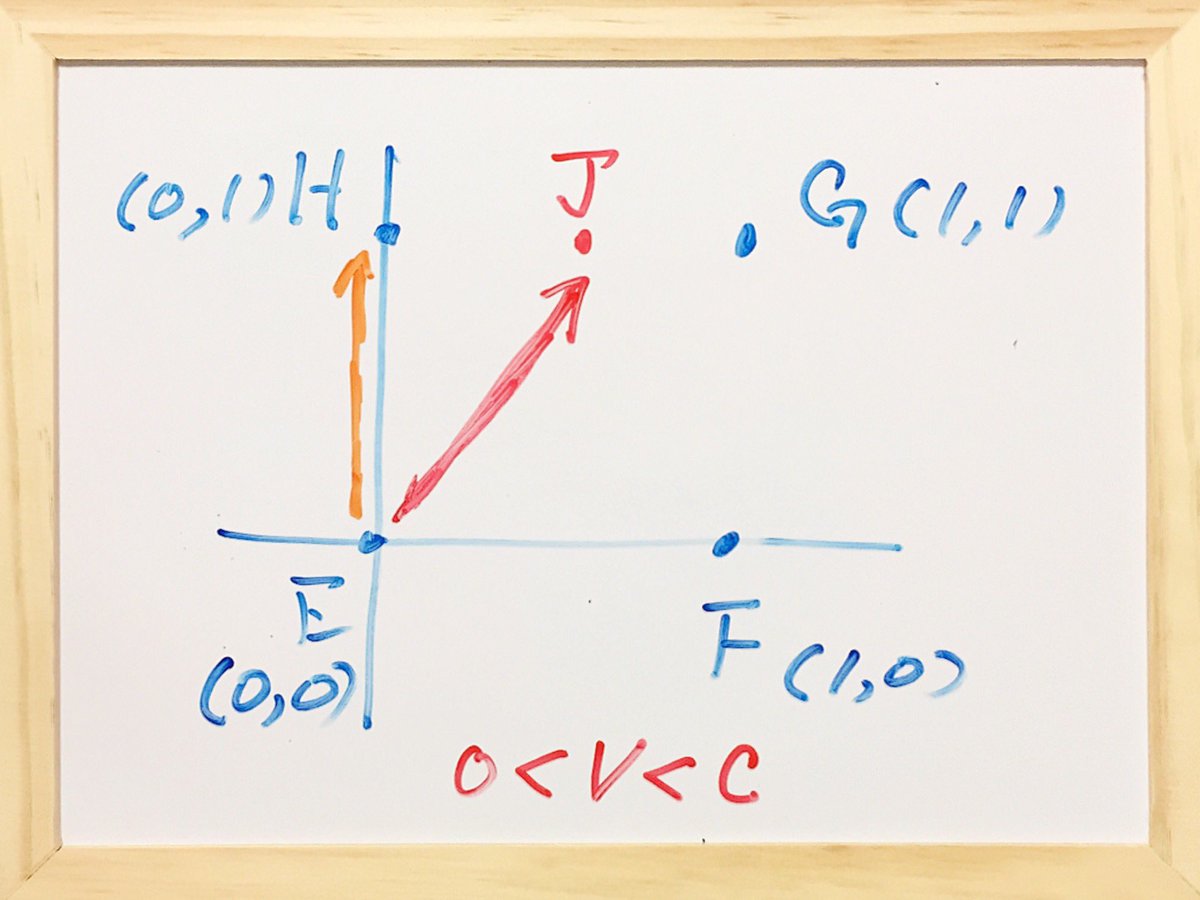 拡大
拡大
 zionadchat
@zionadchat
zionadchat
@zionadchat
数学操作は、上空からの俯瞰や、列車側面をどれだけの奥行き方向の遠さから見ているのか、カメラアイの存在位置を3次元空間内に指定していない。その為に生じたxy平面上の光子軌跡が光速Cを超えたの勘違い。 これに気付いてもらう為に、周囲をウロウロしながら貴殿を追い詰めようとしている。
2017-08-27 02:50:46 zionadchat
@zionadchat
zionadchat
@zionadchat
数学は、手続きなしの光子軌跡認識をする。一方、実験物理では必ずカメラアイ位置を指定して、光子が通過した周囲の漂う空気分子とカメラアイの相対速度をゼロにすることで、光子速度や列車速度や線路速度という、個々の物体イメージによる慣性系速度を相手にしない方法で同時性を記述する。
2017-08-27 02:55:05 zionadchat
@zionadchat
zionadchat
@zionadchat
アインシュタイン氏の論理。慣性系ごとに異なる時の流れがあるという仮説論理を採用してもいいが、その場合でも、ピラミッド頂点から、ピラミッド底面を観察すると、位置EからJに1秒間で情報が伝わったことになる。xy平面上では、位置Eを中心とした半径1光秒を超えるとこに1秒以内に情報は pic.twitter.com/GUHQnOxRLJ
2017-08-27 02:58:28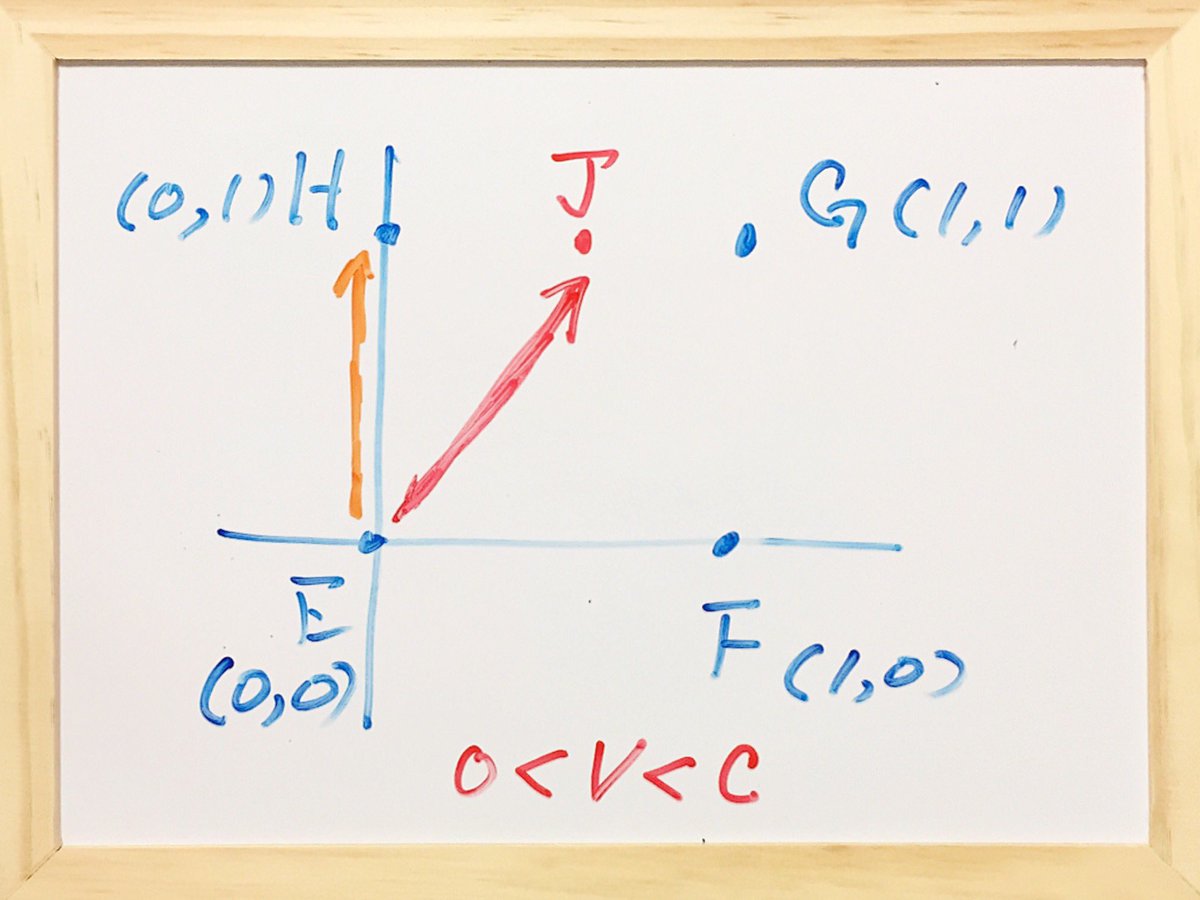 拡大
拡大
 拡大
拡大
 zionadchat
@zionadchat
zionadchat
@zionadchat
伝わらないハズだから、アインシュタイン氏の論法に問題がある。 だが、アインシュタイン氏の論法をピラミッド底面ではなく、ピラミッド底面からピラミッド頂点に向かう情報を運ぶ光子に適用すれば、 アインシュタイン氏の提唱、光速で世界を記述することができる。
2017-08-27 03:00:19 zionadchat
@zionadchat
zionadchat
@zionadchat
それには、1つの思い込みを解体しなければならない。ピラミッド底面が平面であるという思い込み。 数学的には平面。だが実験物理にとって、すべてはカメラアイが摂取した光子1つ1つの過去度合いと方向となる。 方向とは天文台の望遠鏡の上げ下げや回転度合いのこと。
2017-08-27 03:02:42 zionadchat
@zionadchat
zionadchat
@zionadchat
数学は空間や、言葉を扱う。 実験物理は見かけから、想定される過去を地図に描く。 直線や平面ってのは無限の大きさだ。無限はイメージで描くことはできない。だから線分や有限平面を扱う。 数学なら直線や平面という言葉そのものを扱えるが、イメージの世界では、有限化されたものだけ扱う。
2017-08-27 03:05:31 zionadchat
@zionadchat
zionadchat
@zionadchat
ピラミッド頂点を、ピラミッド底面から無限高さにしてみよう。 ピラミッド正方形底面中心Eへの垂線も、ピラミッド4つ角への斜線も、 今やたいした違いはない。 これが従来の地図技法、点光源による無限遠からの射影幾何学とか投影法。 pic.twitter.com/gK6Ru4AwcW
2017-08-27 03:09:13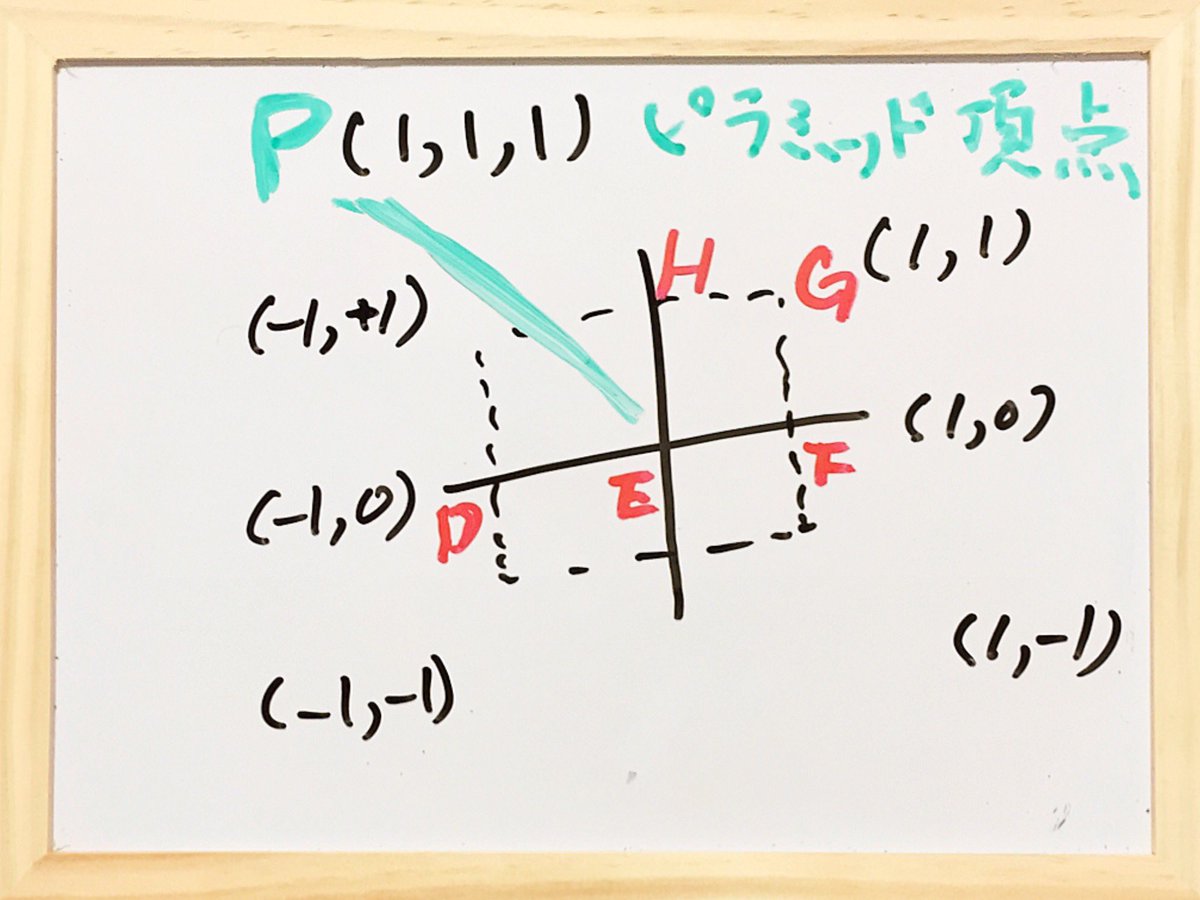 拡大
拡大
 zionadchat
@zionadchat
zionadchat
@zionadchat
でもカメラアイの世界じゃ、現場ピラミッド底面から見える迄の時間、待たなけれなならない。無限遠に局所点を配置すると、いつまで経ってもピラミッド底面見えない。数学の世界じゃ、情報は瞬時に無限遠に到達するけど、電磁現象世界のカメラアイという実験空間の安定状態を常時観察する道具には無理。
2017-08-27 03:13:08 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
そこで、ミンコフスキー時空図を観(み)よう。1次元数直線を扱ったミンコフスキー時空図。 時刻0の数直線。線分DEFの長さは2光秒。 時刻0から時刻1までの間、情報収集する情報将校が位置Eに居れば、 線分DEFの各点の時刻0状態が近接作用で届く。 pic.twitter.com/wsNjRYIapB
2017-08-27 03:39:06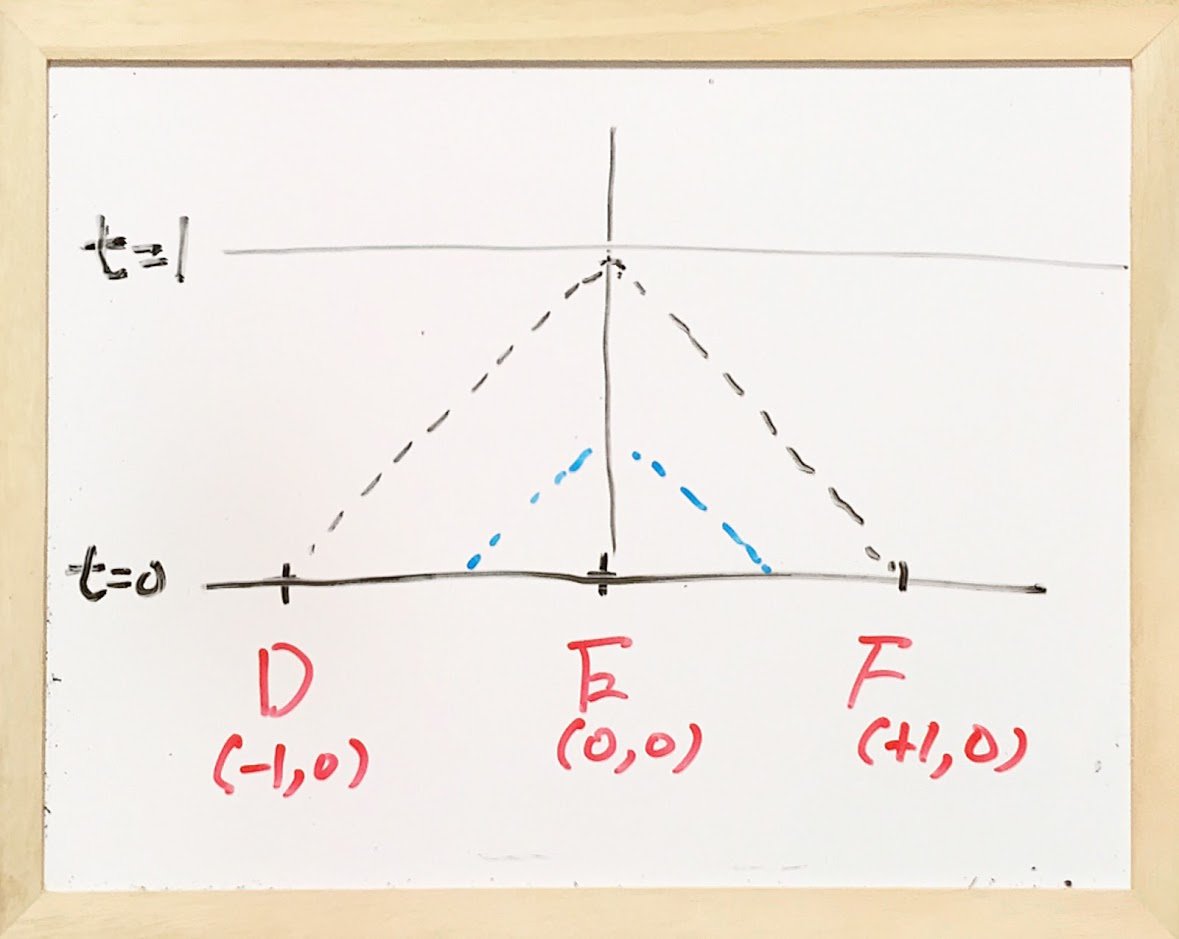 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
線路を走る列車の中間位置、客車中央に存在してみよう。客車中央に立ち、進行方向の先頭車を見る。自分から距離3光秒離れたとこで先頭車のノーズと真下の枕木がほとんどゼロ距離で同居している。と、頭の中でイメージする。 3秒後に見えるハズだと。設計図イメージの世界。想像的座標イメージ。 pic.twitter.com/ZiNLIMppvD
2017-08-27 03:42:17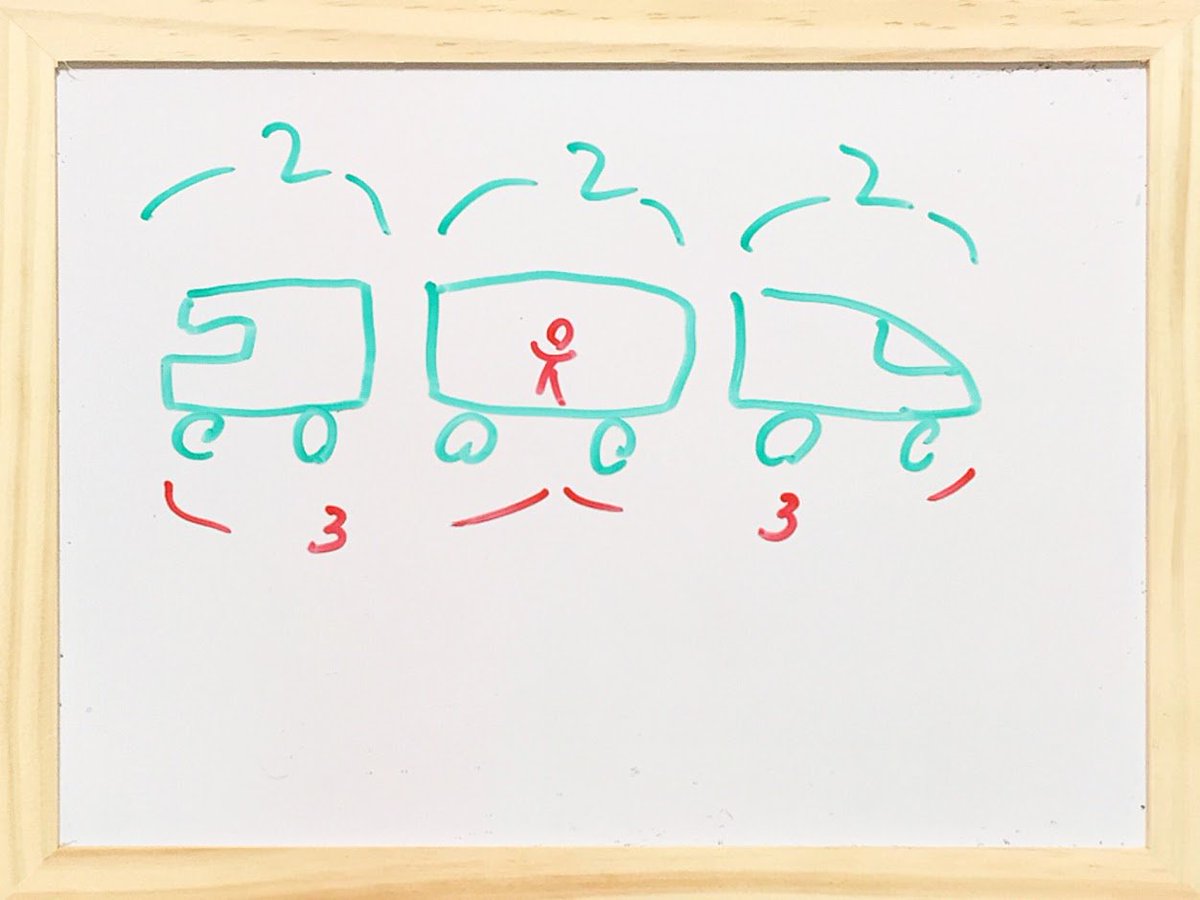 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
だけど、先頭車ノーズは3秒後には、もっと先に進んでいる。客車中央の自分も、3秒後には、もっと右に進んでいる。とすれば、先頭車ノーズと真下の枕木が、ほとんどゼロ距離で同居していた映像が左に進めば、 3秒待たないで、左に進んだ映像情報と右に進んだ客車中央の自分がぶつかる。
2017-08-27 03:45:24 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
線路と光子ペアが母子一体幻想の場合。の、話。母子一体幻想なしの話をするのは、もっと1人称と2人称の組み合わせ紹介してからだから、いまは、線路は光子ペアに対して動いていない母子一体幻想の枠組み、条件内で話をしている。 pic.twitter.com/ehscvhttYW
2017-08-27 03:47:41 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
いままで、線路系から観察すると、列車中央から左右に放たれた光子ペアは、列車両端に同着しない。だけど、列車系では、左右に放たれた光子は同着するを当然としたことで描いていた、特殊相対性理論に出てくる斜行座標が嘘になる。 pic.twitter.com/gWxtc3p03X
2017-08-27 03:56:20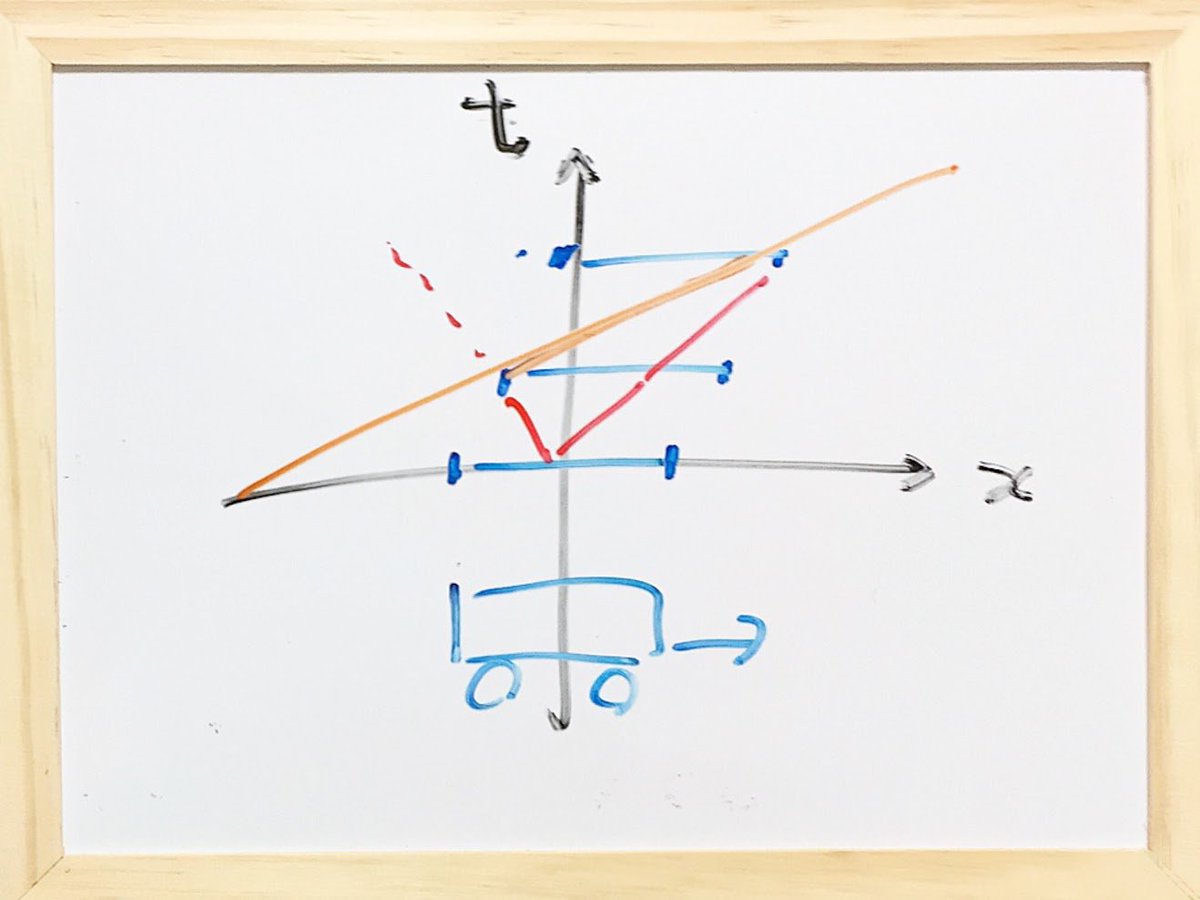 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
素直にミンコフスキー時空図で、線路系基準慣性系なら、相手側列車慣性系数直線が横ズレするだけになる。 線路側からの記述でも、列車側からの記述でも、展望車に光子が先にぶつかる。 pic.twitter.com/PPB24Z5dyC
2017-08-27 03:59:17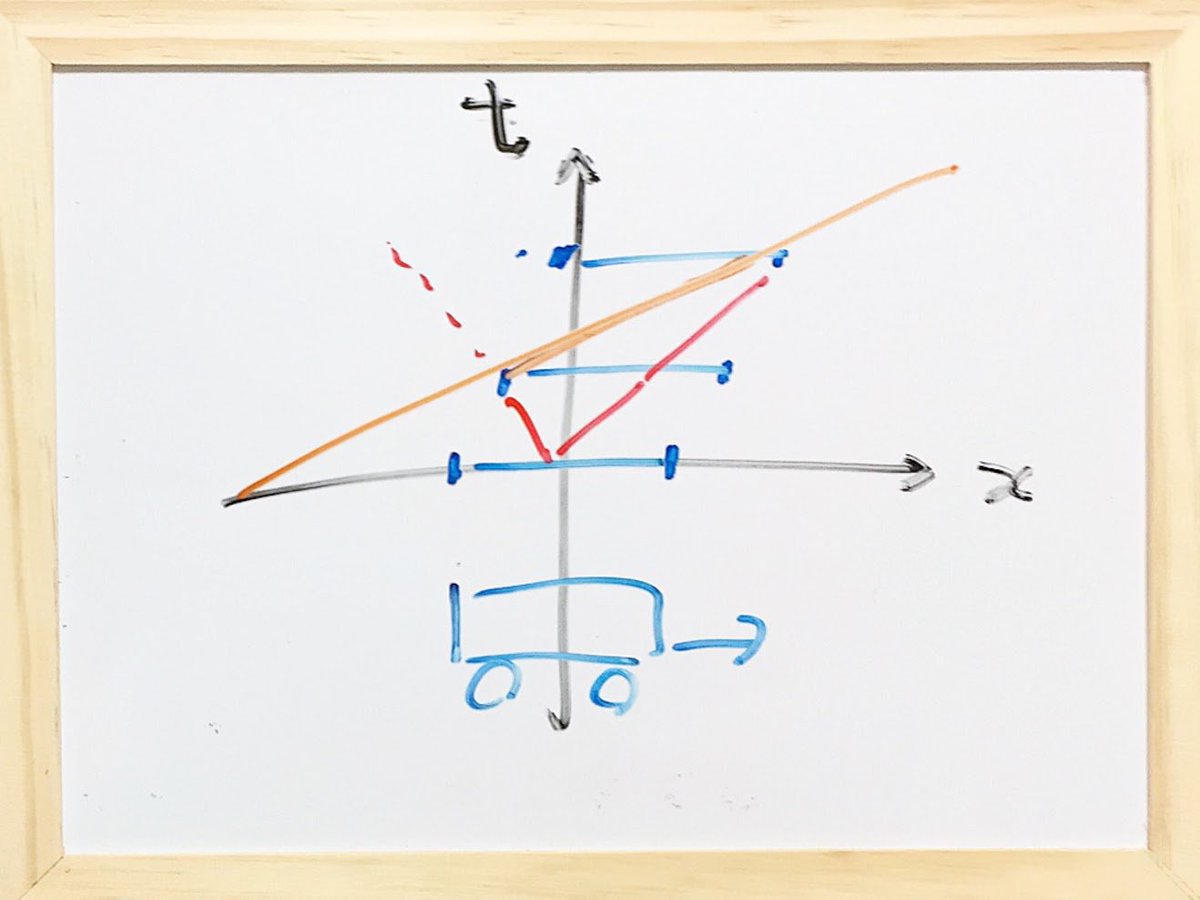 拡大
拡大
 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
逆に、列車慣性系を動かない数直線にしてミンコフスキー時空図に描いたら、横ズレする数直線に線路慣性系がなるというだけ。 この話に納得してもらう為に、1人称と2人称の組み合わせの話をする。 だが重要なことは、数学操作だと奥行や上空高さの具体的俯瞰位置が記述されていなかった。
2017-08-27 04:02:23