-
 zionadchat
zionadchat
- 1210
- 1
- 0
- 0
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
コイルと棒磁石が、x軸を速度Vと速度ーVで動いてる。 コイルの1点をピンクでマーキング。 棒磁石の1点を水色でマーキング。 pic.twitter.com/XRRbGnnFMC
2017-09-12 08:43:36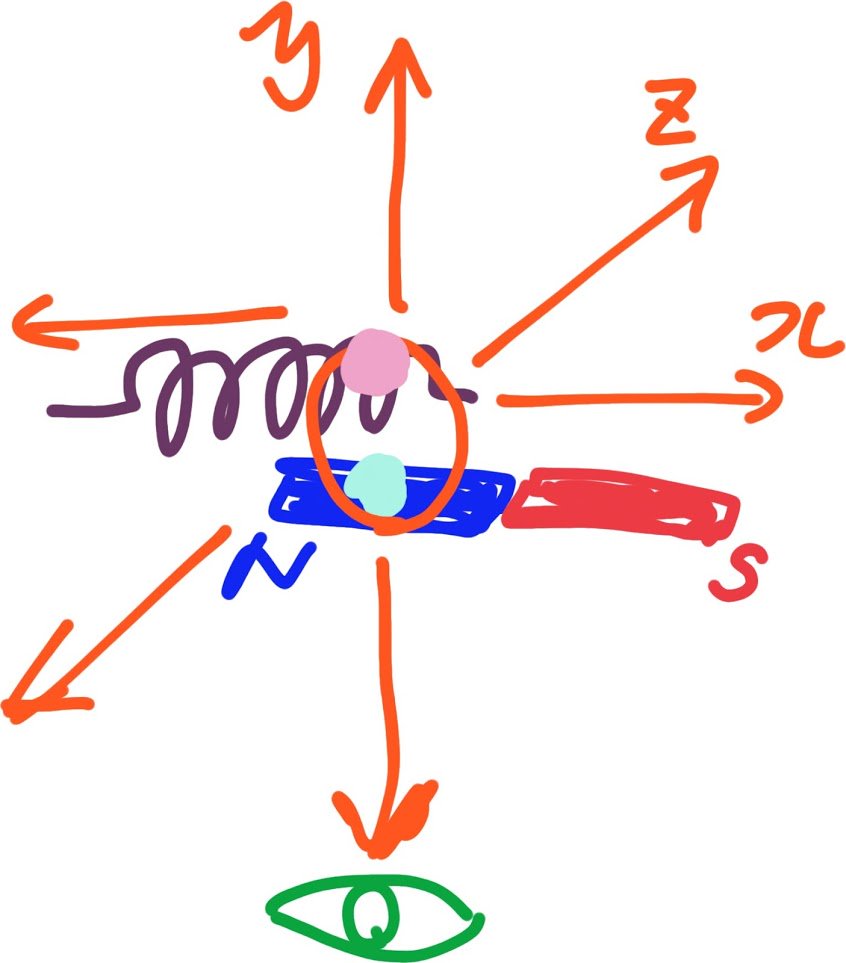 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
絵図をちょっと修正して、 観察者の目玉は、z軸の(0,0,1)。 pic.twitter.com/r4jlVZKy9W
2017-09-12 08:44:24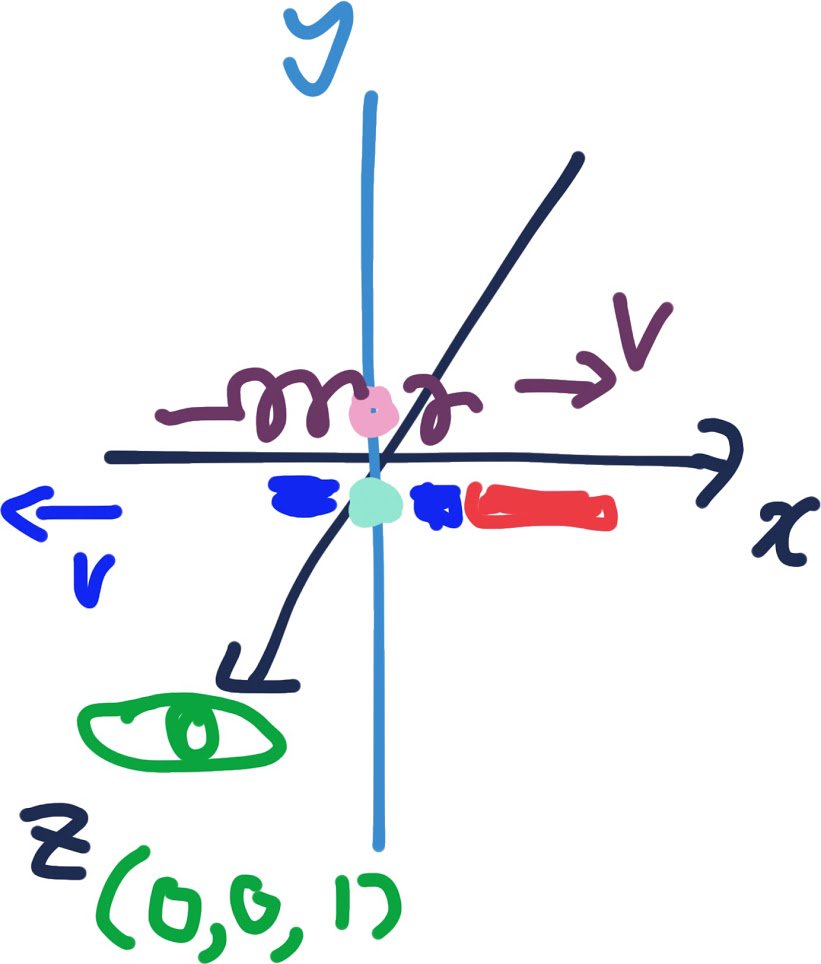 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
時刻0に、(0,0,0)をコイルピンク点と棒磁石水色点が通過同居したのを、カメラアイが、(0,0,1)の位置で、1秒後に確認した。 この座標空間は、時々刻々の光子ペア存在中央を基準慣性系にしてる。 だから「光子は1秒に1」この座標空間を進む。 pic.twitter.com/wTqllaTuRe
2017-09-12 08:47:23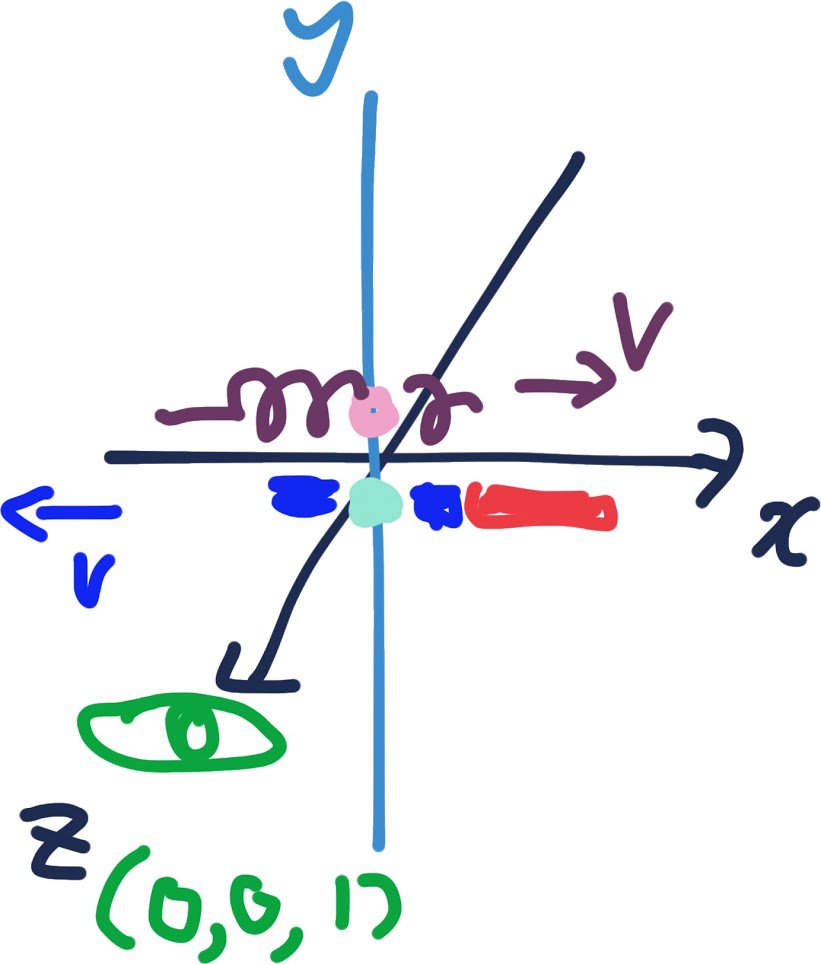 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
コイルを上り列車に見立てて、 コイルは線路レール原子群に対して動いてる。 棒磁石を下り列車に見立てて、 棒磁石は線路レール原子群に対して動いている。 コイルと棒磁石の相対速度は、最大2Cが可能である。
2017-09-12 08:47:44 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
従来の思考実験で、列車基準慣性系を描くと、 線路レール原子が最大速度Cで動く相対速度イメージはあったけど、 上り列車から見た、下り列車との相対速度イメージが欠けていた。 直線型加速器で、電子と電子をほとんど相対速度2Cで、ぶつけてるのにだ。
2017-09-12 08:48:17 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
3次元で考えるのは面倒なんで、x軸に注目する。 ミンコフスキー大先生は、x軸を数直線とし、 x=0に情報が集まる感じにした。 x=0に居れば、区間[-1から+1]の情報が1秒で集まる。 pic.twitter.com/uXixWFUilA
2017-09-12 08:49:50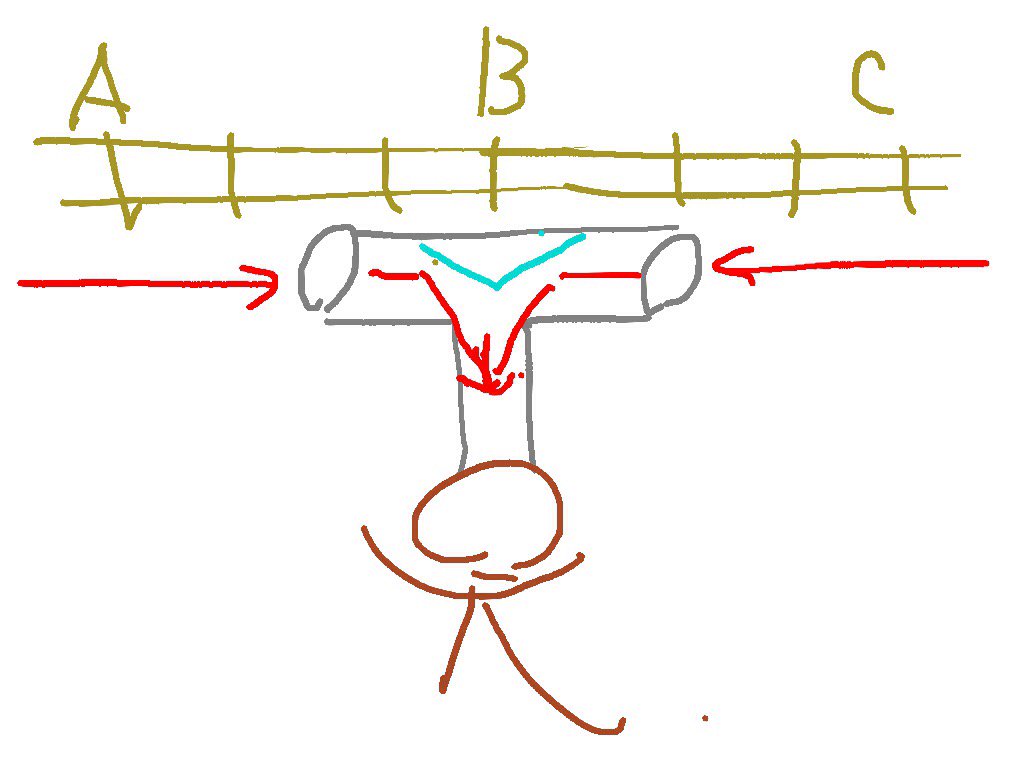 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
遠いとこの時刻-1の情報は1秒後にゲット。 近いとこの時刻-1の情報は0.3秒後にゲット。 とかして、1秒かかって、2区間の「時刻-1」状況を描く。 pic.twitter.com/jObtU60ygh
2017-09-12 08:50:18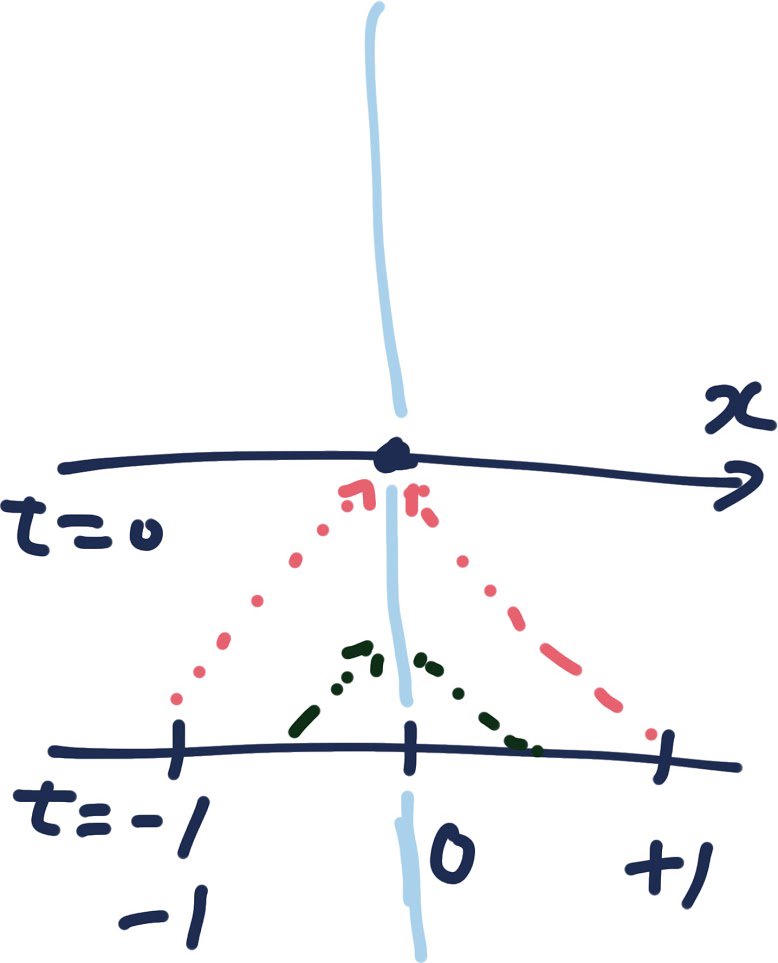 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
しかし、それはコイルや棒磁石が動く実験線路に立つことであって、 観客は、バッターとピッチャーのやり取りを普通は、1塁スタンドか3塁スタンドから観る。 だから、x=0情報が1秒遅れ。 x=-1とx=+1情報が√2秒遅れになる。 pic.twitter.com/HccmB9AQk6
2017-09-12 08:53:46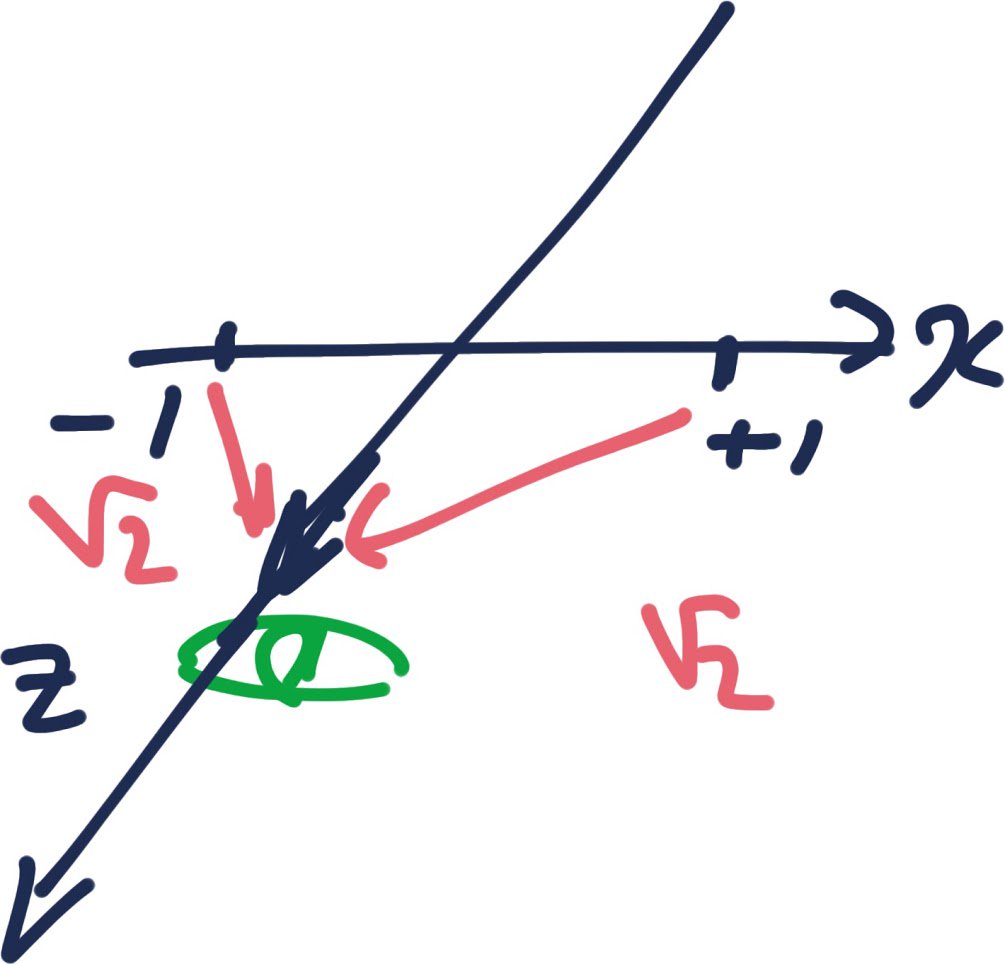 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ピッチャーが光ボールを投げた時刻0。位置x=+1。 バッターが光ボールにバットを当てた時刻1。位置x=0。 とすると、現場では光ボール滞空時間は1秒だけど、 見かけ滞空時間は、観客目玉位置では、
2017-09-12 08:54:34 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
時刻√2に光ボール出発光景届く。 時刻2にバットに光ボール接触光景届く。 で、2ー√2=約0.6秒。見かけ滞空時間。
2017-09-12 08:54:52 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
もちろんこれは観客目玉位置からの見かけ滞空時間だから、 現場時刻に再現すると、 光映像情報入手までに掛かった時間を引いて、 現場時刻0にピッチャーが光ボールを投げて 現場時刻1にバッターが光ボールにバットを当てた。
2017-09-12 08:56:11 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
観客目玉は、光子ペア存在中央基準慣性系に対して動いてないから、 この情報が届く視線距離を逆算するだけでいい。
2017-09-12 08:56:21 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
孫悟空の如意棒のように、左腕を長さ1。右腕を長さ√2。伸ばす。 バッターとピッチャーの位置まで。 pic.twitter.com/70SgKpt21l
2017-09-12 08:56:58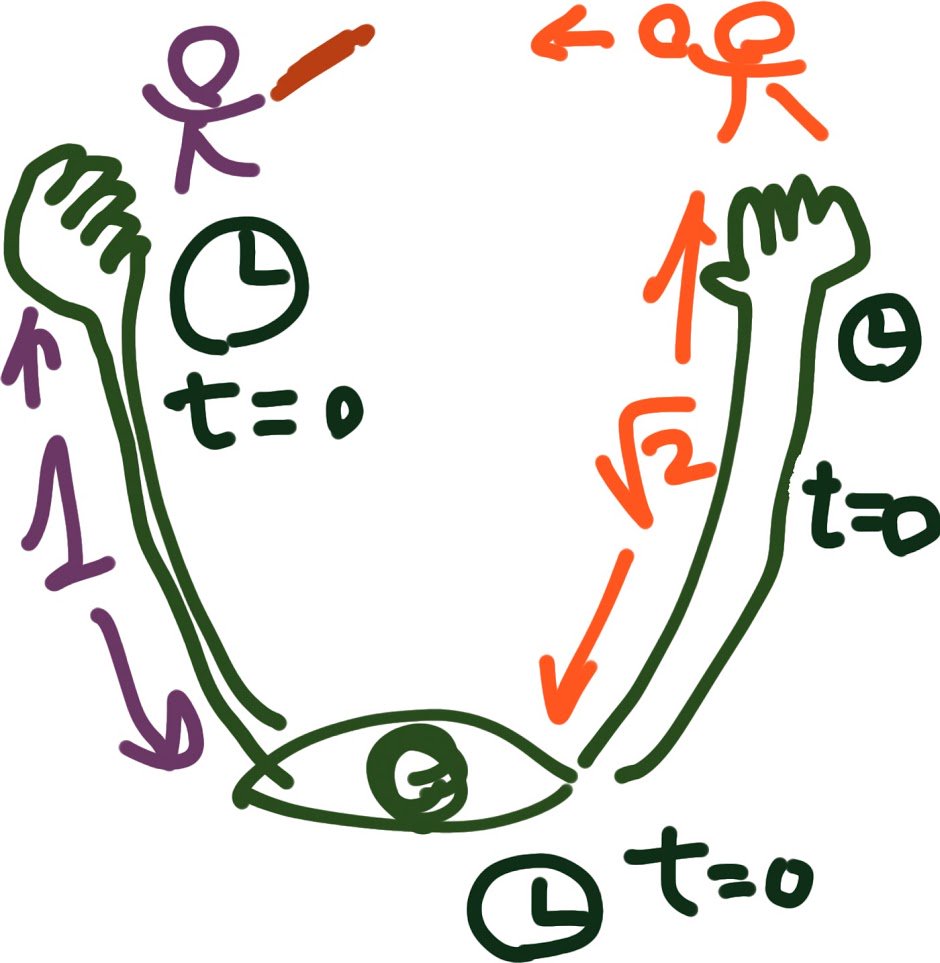 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
両腕に腕時計。観客目玉の脳にも時計。 どれも同時刻。左右腕先と観客目玉は、相対速度0の、同じ慣性系。 ピッチャーが時刻0に光ボールを投げたとき、 座標空間原点に居るバッターが光を反射して、 xyz軸のプラスとマイナス方向に光子ペアを放った。
2017-09-12 08:57:58 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ピッチャーも、時刻0に、己の姿をxyz軸に光子ペアを放った。 目玉観客も、時刻0に、己の姿をxyz軸に光子ペアを放った。 ピッチャーもバッターも目玉観客も、 時々刻々の光子ペア存在中央に対し、相対速度0。
2017-09-12 08:58:18 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ピッチャーは、時刻0に光ボールを投げたの自覚。 光ボールがバットに当たったの認識するのは時刻2。 見かけ光ボール滞空時間は2秒間。 バッターは、時刻1に光ボールがバットに当たったとき、 ピッチャーが光ボール投げた光映像が同時に届く。 だから、見かけ光ボール滞空時間は0秒間。
2017-09-12 08:58:42 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ガンダム世界で、ビームが視認で避(よ)けられるかの話。 超能力ありだから、電磁現象の近接作用で情報入手してるんじゃないようなんで、ニュータイプは。ニュータイプは、数学者か、 未だ知られてない物理現象。量子テレポーテーションかどうかは知らん。
2017-09-12 08:59:01 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
見かけ滞空時間は違っても、 ピッチャーとバッターと観客目玉は、光子ペア存在中央に対し相対速度ゼロなので、視線距離から逆算すれば、 歴史地図としての、同時刻事象を再現できる。どの立場からも。
2017-09-12 08:59:34 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ま、視線距離から逆算しなくても、地面に、地面のあちこちに時計を埋め込んどけば、 ピッチャーが光ボール投げる瞬間の映像内に時刻0が地面に表示されていれば、 バッターは、ピッチャーが光ボール投げる瞬間の現場時刻を逆算で求めなくても、いいことになる。
2017-09-12 08:59:54 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ここまで、あたりまえの話をした。 座標空間内の局所点存在であるバッターやピッチャーや観客目玉は、光ボールの見かけ滞空時間から逆算して、或いは、光映像内にある地面に埋め込まれた現場時刻表示の時計を見て、 数学的な同時刻、ミンコフスキー時空図の時刻0平面が、やっと描けた。 pic.twitter.com/lKa9DcOvib
2017-09-12 09:00:25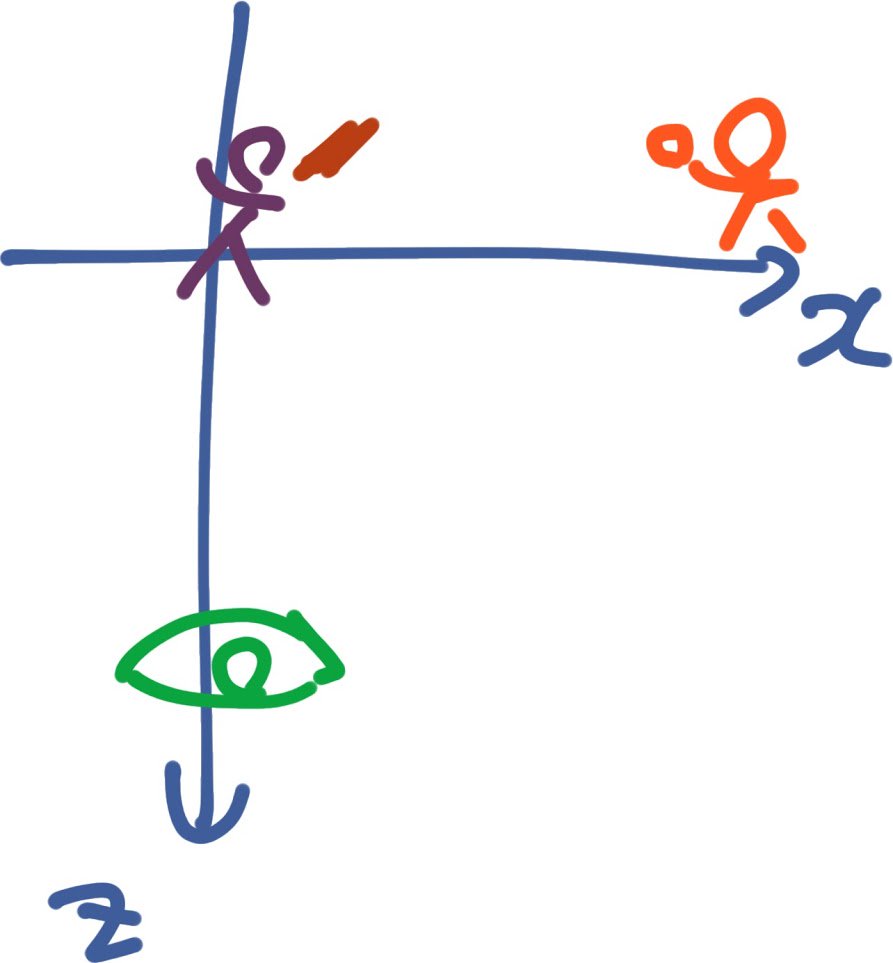 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ただし、ピラミッド頂点から見ると、 ピラミッド底面2x2の正方形に内接する円だけで、 数直線区間(x,z):(-1,0)から(+1,0)は 過去光円錐底面に入るけど、 (+1,+1)とかは、外接する円を用意しないと、入らない。 pic.twitter.com/Aml9NR01Fw
2017-09-12 09:01:29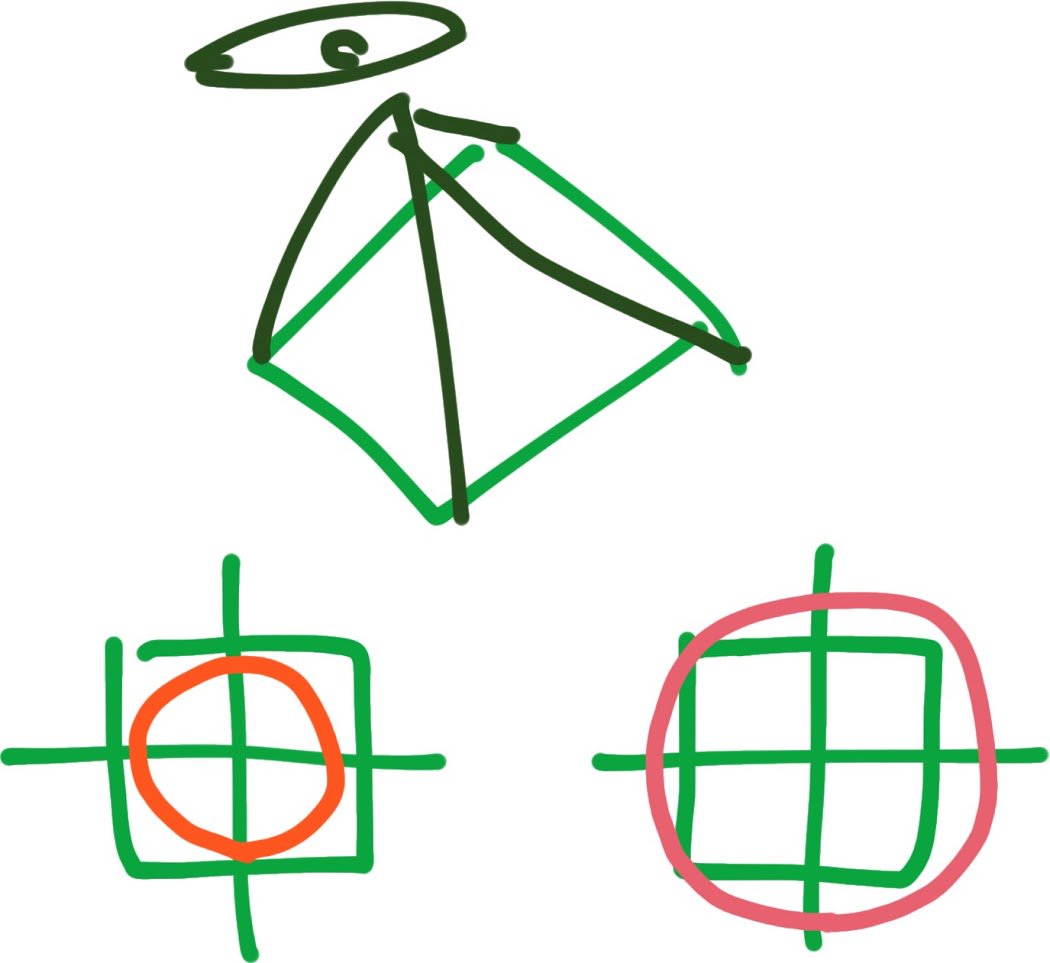 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
いままで、列車に載せた光時計筒内を線路系から見て、 1秒で光時計筒の床から天井まで移動する軌跡が見えると 思い込んでいたハズだけど、それって不可能じゃん。 だって、ピラミッド底面中心に現在時点となる情報集積地を置けば、 (+1,+1)からの情報は、√2秒待たないと見えない。 pic.twitter.com/umbV9HUnE8
2017-09-12 09:02:21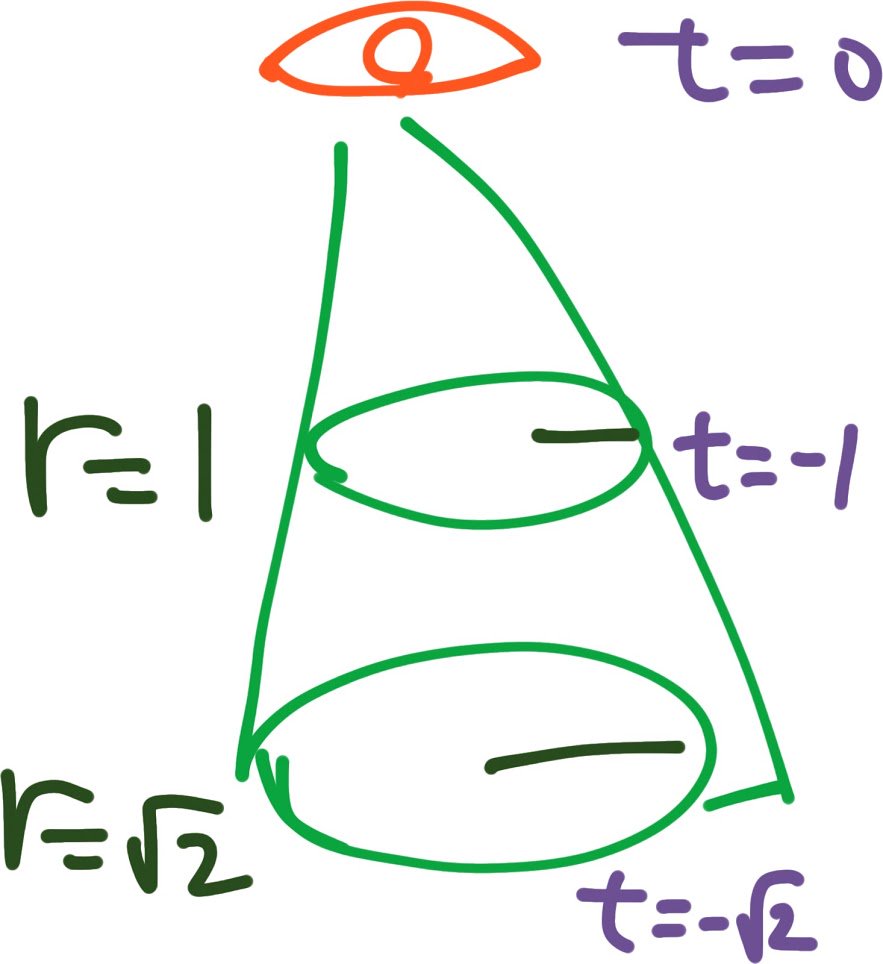 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
見えないけど光時計筒天井は、時刻1に(+1,+1)に存在する。 時刻0に光時計筒天井は(0,+1)を通過してるから。 光時計筒横ズレ速度を光速Cに固定して話を単純化する。 pic.twitter.com/8vy4K8r3ix
2017-09-12 09:30:29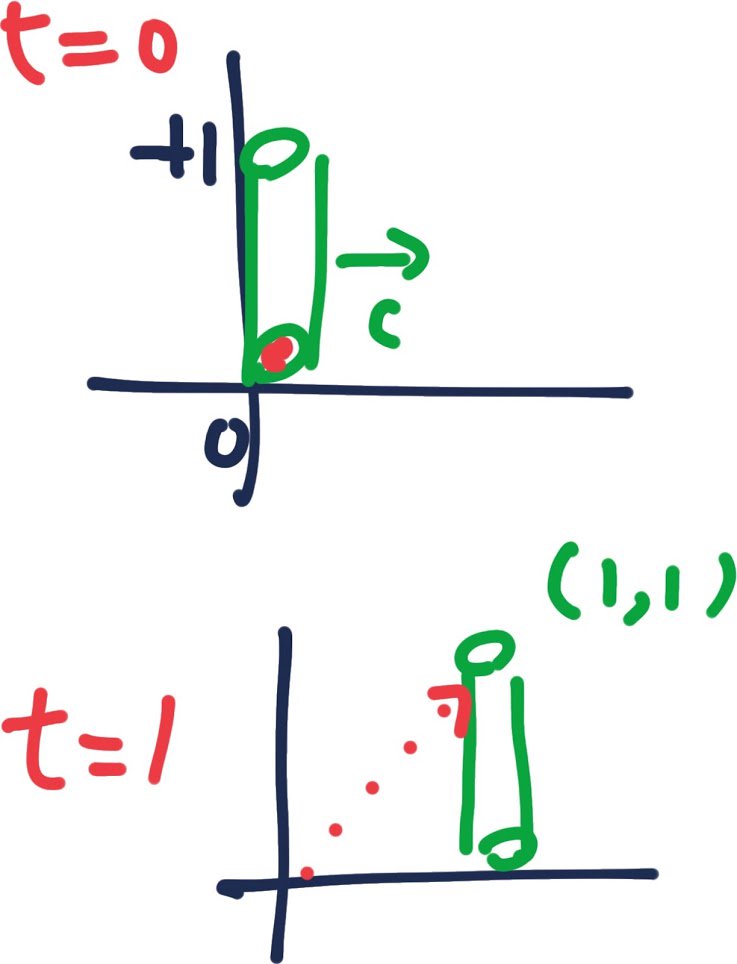 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ところで、いままでこの図を、列車内光時計筒として見てきた。 これを列車慣性系から見た、京都駅ホーム内光時計筒として見るとどうなるだろう。
2017-09-12 09:04:47 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
下り列車内から京都駅ホーム内光時計筒を見る。 下り列車内から真下を見る。線路枕木が左から右に流れて見える。 京都駅ホーム内光時計筒も右に流れて見える。 時々刻々の光子ペア中央と線路慣性系は同じ慣性系。 pic.twitter.com/HUvBV2SiMz
2017-09-12 09:05:29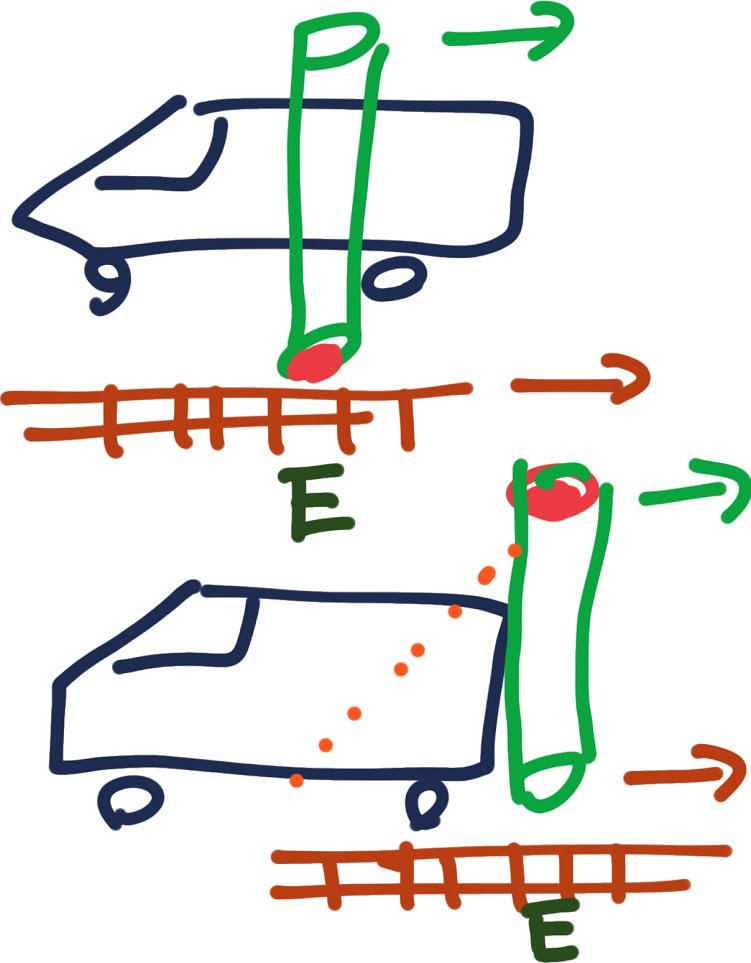 拡大
拡大