-
RascalTaku
- 188189
- 327
- 235
- 168
-
- いいね！168
CHARTMAN
@CHARTMANq
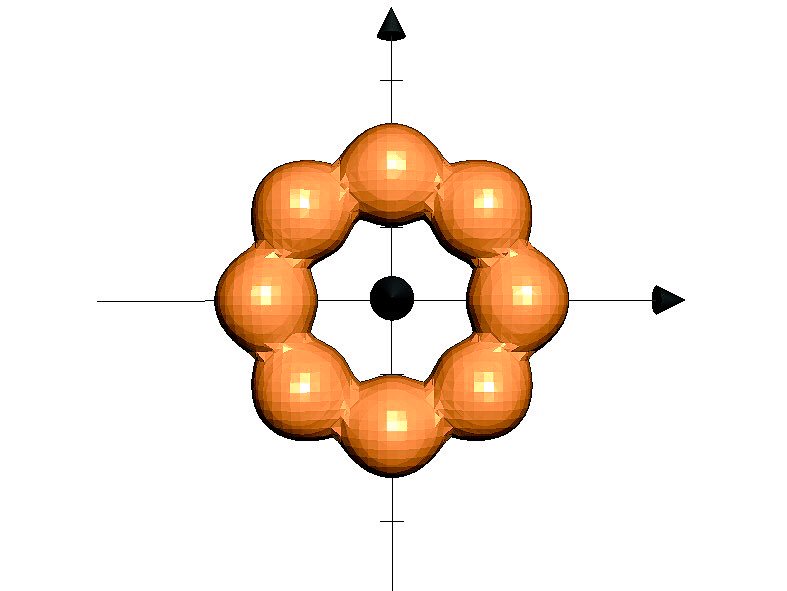
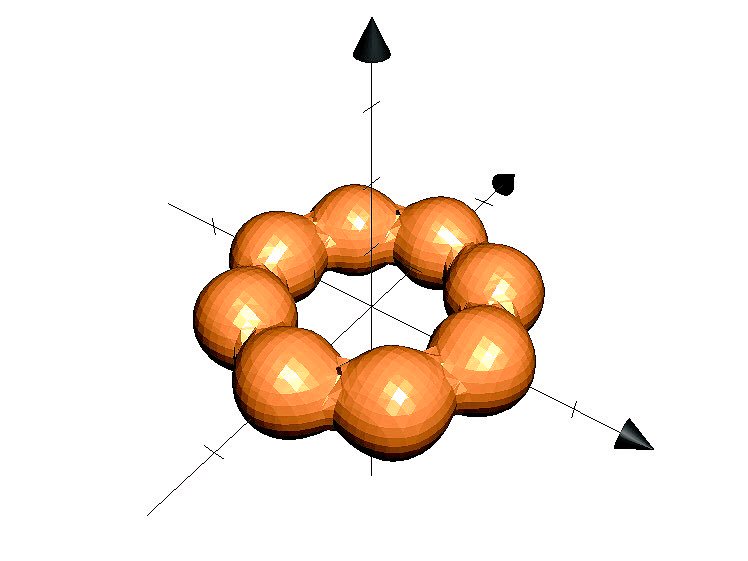
3時間に及ぶ試行錯誤の末，たった1つの数式で3Dの「ポン・デ・リング」を表示することに成功．(2Dのもあるよ) pic.twitter.com/r23phIA4hp
2017-12-27 21:51:50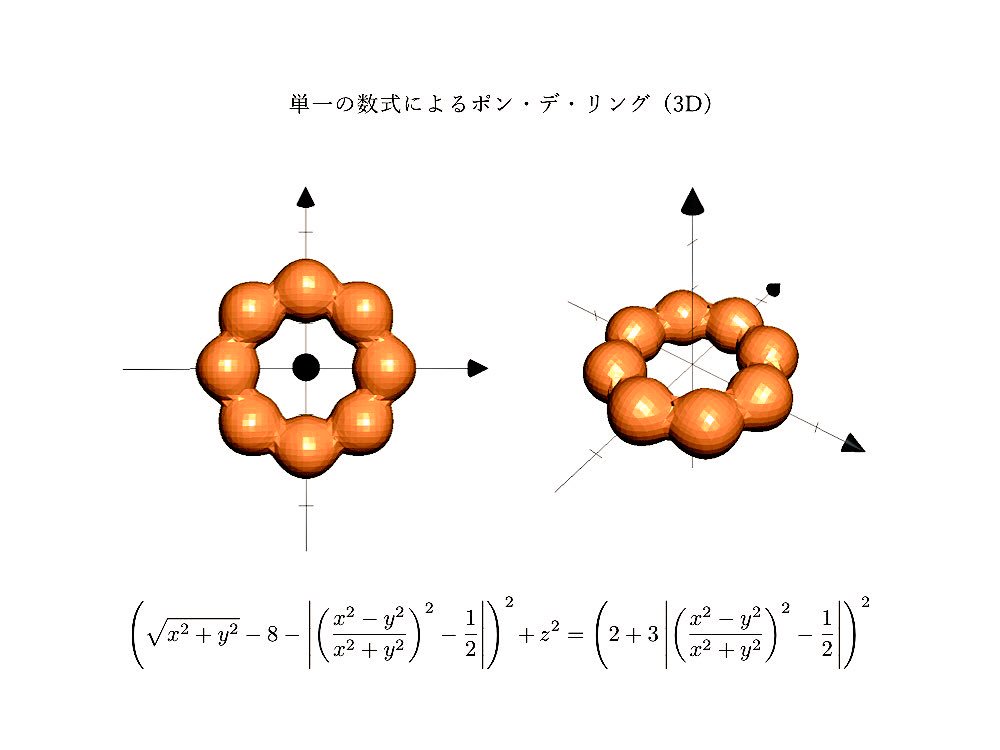
拡大
拡大
拡大
拡大
CHARTMAN
@CHARTMANq
「おっぱい関数の人か」という意見が出ておりますが，その通り，名古屋大学代表のあの人です． 「"お城"スコープの人か」という意見も出ておりますが，その通り，レポートにお城を召喚したあの人です． またくだらないことをしでかしましたが，あたたかく見守ってやってください(^_^;)
2017-12-28 00:47:24「おっぱい関数」とはこちらのこと
CHARTMAN
@CHARTMANq
「大学対抗おっぱい関数選手権大会」遂にトップ10発表！ 私(名古屋大学)の「揺れるおっぱい関数」がランクインしました( ･ω･ )ﻭ✧ 記念に誰でも"触れる"ようにしたので、是非ご自身の手で動かしてお楽しみください(^-^) →desmos.com/calculator/i05… pic.twitter.com/0yvKDhYy9y
2017-10-24 19:59:09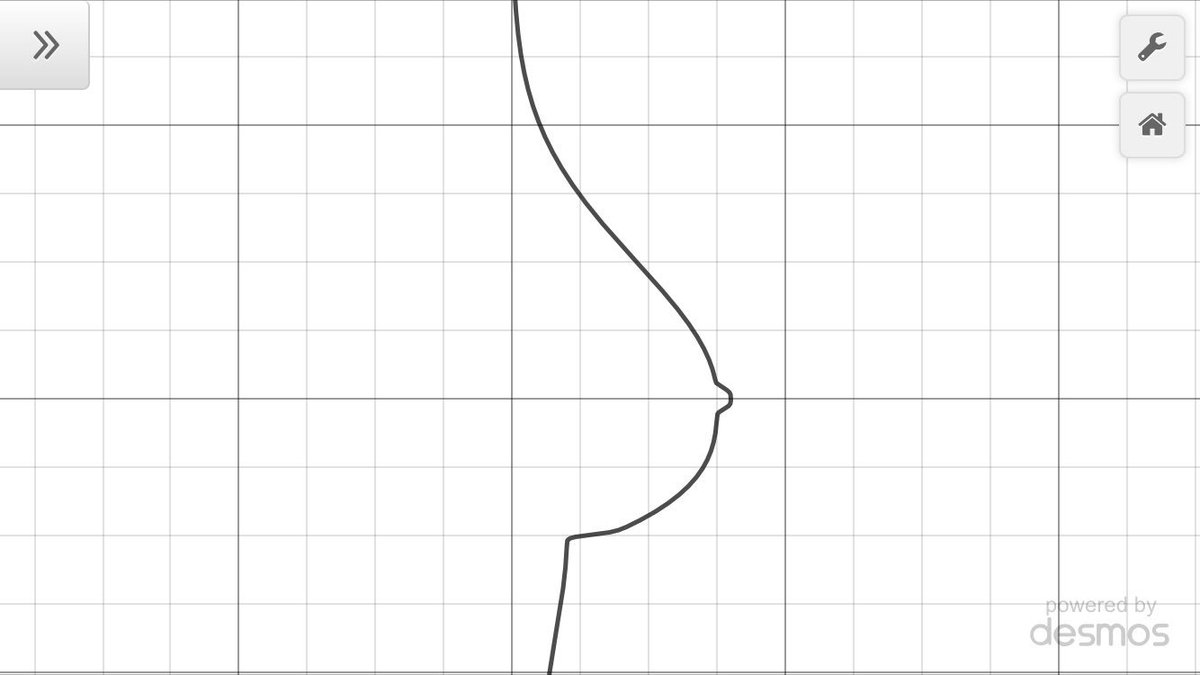
拡大
だいぶ前のまとめですが、人類はこうして試行錯誤しています
世界は数式でできている（おっぱい編）
さすが資生堂さんは良いこといいますね♪
他にも数式やグラフがあったと思うので、見つけ次第追加していきます。
31783 pv
152
2 users
60
それにしてもすごい
かな
@kknanoha1
@CHARTMANq @misterdonut_jp しゅごい…こんな時間になんと飯テロを…！！ ただ単に球を8回の回転対称に並べたってわけでもない感じだろうか。一つの式だけってのがまたすごく良いなぁと思った。なんという飯テロを…！！
2017-12-27 21:58:35
Naohiko Yamaguchi
@nycity1022
これはおもしろい。左辺の８がつながる球の数?と思ったが、まさかそんな単純じゃないだろうなぁ。球の数を変数にして一般化するとどんな式になるだろうか？ twitter.com/CHARTMANq/stat…
2017-12-27 22:24:39（数式が理解できる方々との）質疑応答
CHARTMAN
@CHARTMANq
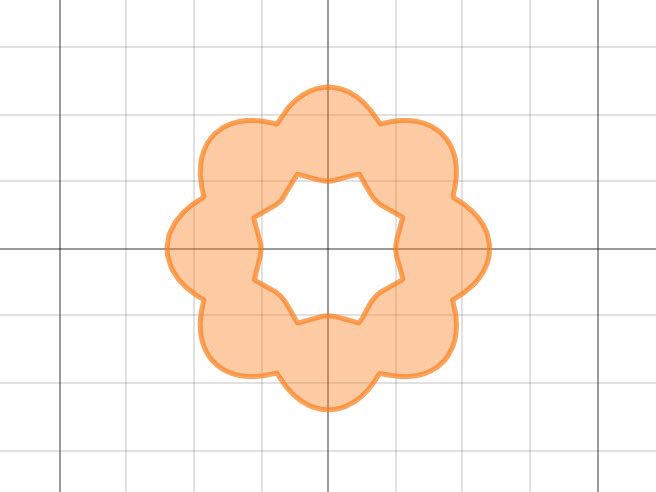
@Rinto11080426 2Dの領域は，極座標を用いて (r-2|cos4θ|-10)(r+|cos4θ|-6)≤0 と表されます(^-^)
2017-12-28 09:21:27
さくらんぼ
@yamashinzyu
@CHARTMANq ff外から失礼します 上の式はx yについて対称なので x=rcosθ, y=rsinθ とした円柱座標系のほうが美しくまとまるのではないでしょうか？ もしかしたらプロットツールや単に好みの問題かもしれませんが、思い付きでいってみました
2017-12-28 01:42:24
CHARTMAN
@CHARTMANq
@yamashinzyu よい質問ですね． 2Dで考える→3Dに拡張 という手順で作りましたが，2Dでの作業中は極座標を用いていました． 3Dに拡張する際，自分が既に知っていたxyz系のトーラス面(最も単純なドーナツ形のものです)の方程式を利用したかったため，xyzに変換して完成させた次第です．
2017-12-28 02:30:55
CHARTMAN
@CHARTMANq
@yamashinzyu また，円柱(円筒)座標系や球面座標系は馴染みが薄いと考えられるので，より多くの人に(式を見たときに)「なんとなくわかる…？！」と思ってもらうには直交座標系で表すのがよいと考えました．
2017-12-28 02:37:35
CHARTMAN
@CHARTMANq
@ktflight_mig21 2Dの領域は，極座標を用いて (r-2|cos4θ|-10)(r+|cos4θ|-6)≤0 と表されます．こっちはかなりシンプルですね(^-^)
2017-12-28 12:05:32
CHARTMAN
@CHARTMANq
@jiro_inazuma いろんな人の目にとまり，こういうのをキッカケとして数学好きな若者が増えると嬉しいですなぁ(by 20歳のおじさん)
2017-12-27 22:37:50