math_neko -
- いいね！0
後ほど登場します > ワヘイヘイ漫画
ということなので、場所(と適切な謝礼)を用意すれば alg_d 先生の生の圏論のお話が聴けるかもしれません(保証はしませんが)。
V-alg-d
@alg_d
今、条件を3つの式で書いてしまいましたが、圏論っぽく(?)図式で書くと次のようになります。(Cが射の合成を与える写像で、I^a: 1={*}→Hom(a, a) は I^a(*) = id_a となる写像) pic.twitter.com/6TbuQxbuuc
2018-01-01 01:44:28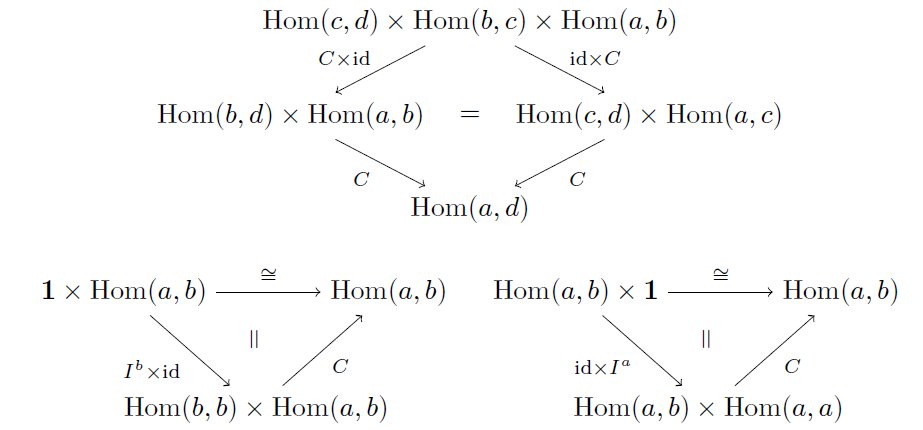
拡大
V-alg-d
@alg_d
さて続きましてstrict 2-categoryというものがあります。これはざっくり言うと、圏という概念に2-morphismというものを追加したものです
2018-01-01 01:48:07
V-alg-d
@alg_d
2-morphismというのは、dom, codが一致している二つの射f, gがあったときに、「fからgへの射」のようになっていて、図式では次のような感じで書きます。σが2-morphismです。(2-morphismは「2」なので2本線の矢印で表します) pic.twitter.com/n4TAZ0FmvG
2018-01-01 01:53:26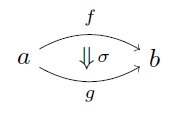
拡大
V-alg-d
@alg_d
そして、通常の圏と同じように、この2-morphismが満たすべき条件が色々と与えられたものがstrict 2-categoryです
2018-01-01 01:54:12
V-alg-d
@alg_d
つまり例えばどういうことかというと、3つの射f, g, h: a→b があって、2-morphism β: f⇒g, γ: g⇒h があったら、このβとγは「合成」できなければなりません。更に、この「合成」について結合律と単位元の存在が成り立つ必要があります。 pic.twitter.com/3qy2woJvI4
2018-01-01 01:58:28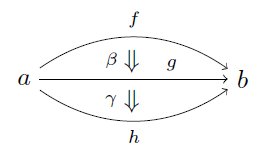
拡大
V-alg-d
@alg_d
この合成を垂直合成と呼んでalg_d.comではγ*βで表していますが、この記号は今日は使わないと思います pic.twitter.com/hRNZQTCgyq
2018-01-01 02:00:44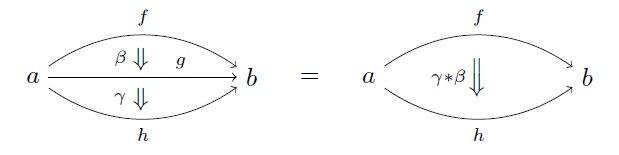
拡大
V-alg-d
@alg_d
さて、strict 2-categoryには他にも条件がまだあって、今Hom(a, b)が圏になるという条件があったのですから、当然合成を与える C: Hom(b, c)×Hom(a, b)→Hom(a, c) も関手になるという条件が加わります。(もちろん先程と同じ可換図式も要求します)
2018-01-01 02:03:52
V-alg-d
@alg_d
まったく同じ図式だが「写像の図式」から「関手の図式」にパワーアップ(?)している pic.twitter.com/ATM83snlPm
2018-01-01 02:05:43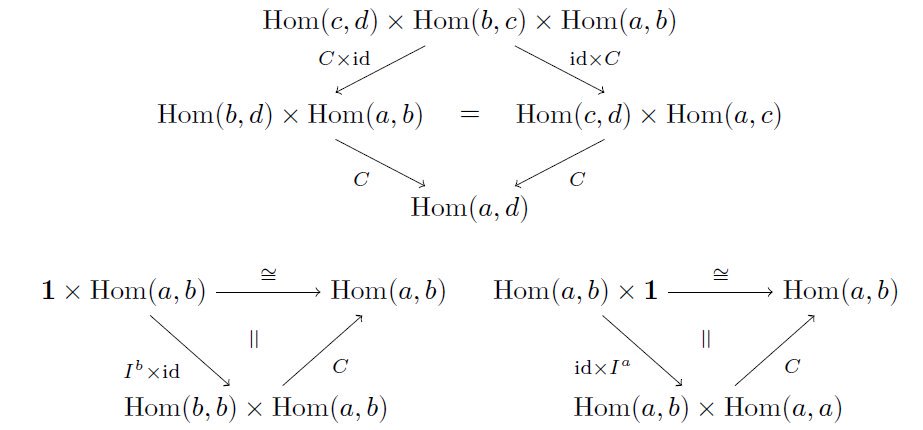
拡大
V-alg-d
@alg_d
さて、strict 2-categoryの定義は大体こんなイメージ(2-morphismというのが加わっていて、それなりの良い条件を満たしている)ですが、ここで先程の図式をよく見ると「関手の可換図式」つまり「関手の等号」が成り立つことを要求しています。
2018-01-01 02:10:22
V-alg-d
@alg_d
しかし圏論をやっていればご存じの通り「関手の等号」というのは相当強い条件であるので、ここは「関手が同型(自然同型)であればよい」という条件に弱めたくなるのが人情(?)です
2018-01-01 02:11:09
V-alg-d
@alg_d
そこで、そのように弱めたもの(ただし、代わりに+αの条件は付けくわえる)をbicategory (weak 2-category)といいます。
2018-01-01 02:12:27
V-alg-d
@alg_d
つまり、このように「次の自然同型α, λ, ρが与えられている」という風に弱めます。 pic.twitter.com/ARPPS8aK4o
2018-01-01 02:15:25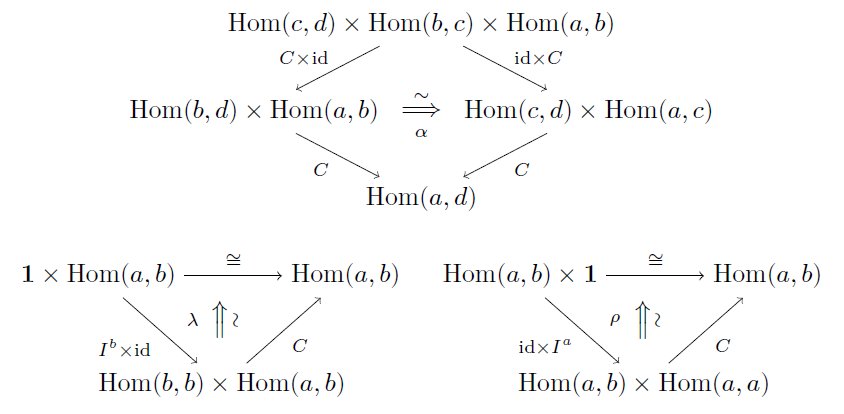
拡大
V-alg-d
@alg_d
このように弱めると、例えば3つの射 f: a→b, g: b→c, h: c→d が与えられたとき、自然同型αの「<h, g, f>成分」は同型 α_{hgf}: (h・g)・f ⇒ h・(g・f) となります。(自然変換の定義に戻って考えると分かります。)
2018-01-01 02:17:53
V-alg-d
@alg_d
言い換えると (h・g)・f とh・(g・f) が同型になります。つまり、bicategoryでは「結合律が同型のレベルであれば成り立つ」という条件になっていることになります。
2018-01-01 02:19:03