-
- いいね！178
三崎律日
@i_kaseki
小学3年生の女の子の自由研究で、「じゃんけんの手はなぜ3種類しかないのか」というテーマで、3種4種5種…と順に勝ち負けのパターンを書き並べていき、最終的に 「奇数個の手ならば勝ち負けが公平になる」 「5個以上になると勝敗の組み合わせを覚えられなくなる」 という結論まで至っていて感心した。
2018-08-19 09:02:00
三崎律日
@i_kaseki
これはワイドショーの「自由研究特集」での一幕だったんだけど、↑の研究に対するコメンテーターの反応が対照的で、「今後この子が数学に触れたら、ｎ個の手の時でも常に成り立つか証明が出来るかも」と言う人と、「これが分かると何か役に立つのか」と疑問視する人がいた。
2018-08-19 09:07:15
三崎律日
@i_kaseki
ちなみに証明は簡単で、N個の手から一つの手を選び、残りのN-1個の手に対する勝ち負けを割り振ると、N-1が偶数でなければ勝敗が偏ってしまう。よってNは奇数でなければならない。
2018-08-19 09:16:11※参考リンク
三崎律日
@i_kaseki
実際、海外には5種、7種のじゃんけんが存在するが、見てのとおり複雑で、3種に収束する気持ちがよくわかる。 pic.twitter.com/AubXQFqy6T
2018-08-19 09:09:52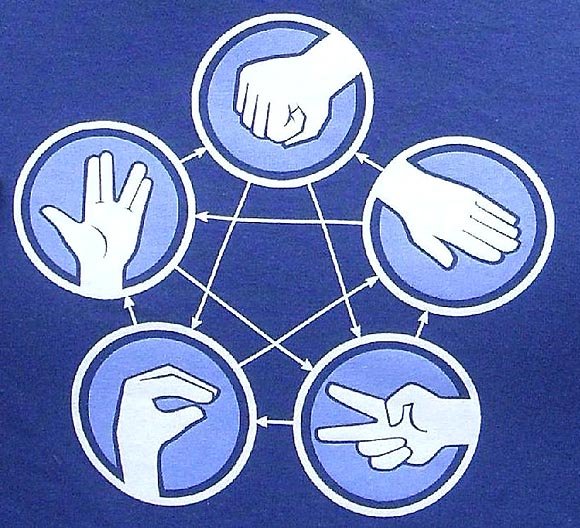
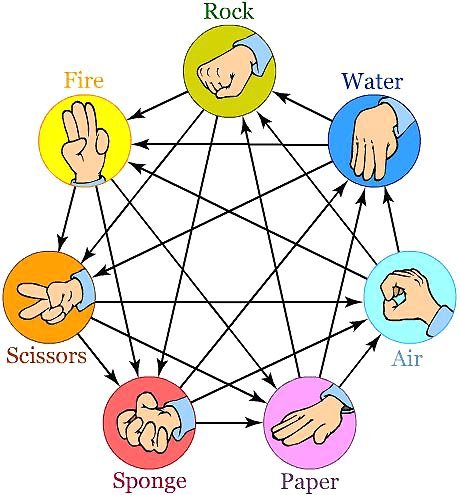拡大
拡大
三崎律日
@i_kaseki
現状最大と思われるじゃんけんの手は101通りで、実に5050通りの勝敗パターンをすべて定義した暇人がいる。 umop.com/rps101/rps101c… pic.twitter.com/zNG5F7pVIQ
2018-08-19 09:22:50
拡大
※リンク先英文です
※これらのルールについての日本語の記事
※Wikipediaも参考までに。
は°は°ん
@hitoyasumiZZZZ
フランスのじゃんけんは出す手が４つもあるらしい。 井戸、石、枯れ葉、ハサミ。 井戸は石とハサミに勝って、ハサミは木の葉に勝って、木の葉は井戸と石に勝って、石はハサミに勝つって、、 ややこしくない？ ３つでよくない？
2018-08-18 14:58:18
は°は°ん
@hitoyasumiZZZZ
じゃんけんって日本生まれなんだって。つまりフランス人が４つに増やしたんだな。 石がグー、枯れ葉がパー、ハサミがチョキはわかるとして、なぜ井戸を足したの？なんで？？
2018-08-18 21:28:04
あみ
@ami19780909
もちろんその小学生は尊敬する。他のひとがどうでも良い事でも自分にとって大事なことを一生懸命する子はえらい。という意味で呟きました。
2018-08-17 13:26:58※関連まとめ
1991年からサザエさんのじゃんけんの手だけを記録して研究発表した同人誌の狂気がやばい「最後の最後であふれる強者感」
静かで良質な狂気を感じる
150758 pv
484
303 users
684