本邦ではその半分なのでガセビア、川の長さと円周率の特にない関係性について

そういえば川の長さが直線距離のπ倍って話だけど、ググってみるとπ/2と記述してるサイトもある。学校での円周率の授業での資料なので、“ガセビア”は載せられないのであろう。

2019-09-02 00:56:39

以前河川の曲がり具合の平均が円周率に一致しますという文献を見たことが有るので... detail.chiebukuro.yahoo.co.jp/qa/question_de… #知恵袋_ π/2派

2019-09-02 01:25:23

川の長さと水源から河口までの直線距離の比はπ？ - kkyamasita's blog kkyamasita.hatenadiary.jp/entry/20060608…

2019-09-02 01:25:36

宮城教育大学機関リポジトリ教材開発の原則 : 「円周率」の学習プラン core.ac.uk/download/pdf/5… 半円の連続でπ/2派

2019-09-02 01:26:54

ちなみに宮城教育大学最寄りの広瀬川や本流の名取川は直線形状なので、1.2倍程度ではないだろうか。

2019-09-02 01:31:29

特急彩雲 @Tokkyu_Saiun

試しに木曽川（長さ229km）でやってみたけど約1.58であんまりπに近くなかったんだよなあ twitter.com/asunokibou/sta…

2019-09-01 01:59:16

マイク @hnakata_JP

πに近い数になるような水源を選ぶってこと？まあ、選べるってるのは自明じゃないね… twitter.com/asunokibou/sta…

2019-09-01 11:14:50

ちきんたお @cs_physics

以前、実際いくつか有名な川で調べてみたら全く成立してなくて残念に思ったことがあります。πではなくπ/2くらいならありそうですが... twitter.com/asunokibou/sta…

2019-09-01 11:23:29

これ、それっぽいけど間違ってると思う。　川の蛇行比は相当ばらけてるように感じるし、πに収束するのかね。 twitter.com/asunokibou/sta…

2019-09-01 11:55:27

@kimi_lica @kiruria281 @asunokibou 本邦だと勾配が強くて流速が速いので、河道は直線化しちゃいますねぐにゃぐにゃだった石狩川だと直線距離で150kmのところ、河道長は自然状態で360kmがショートカットの工事をして268kmに。半円を左右に繋げた形だとπ/2で、それが妥当なところで。

2019-09-01 15:55:34

Tellur @Tellur128

迂闊に信じてはいけない話。河川によってバラツキが非常に大きい。淀川(高時川から)が約1.3。利根川や長良川、富士川だと約1.5。信濃川(千曲川を含む)や木曽川で約1.6。最上川が約1.7。阿賀野川が約1.8。石狩川や筑後川が約1.9。球磨川が約2.6。江の川が約3.8。 twitter.com/asunokibou/sta…

2019-09-01 12:09:44

@asunokibou これ根拠あるんですかね… 一見「なんかそれっぽい」ように感じてしまいますが例えば、日本最長の信濃川長さ367km 直線距離ざっくり228km 比1.6 北海道最長　石狩川長さ 268km 直線距離　ざっくり138km 比1.9 ナイル川　6695km 水源3600kmぐらい？比1.9 3.14の根拠がわからんのです。

2019-09-01 12:40:43

@LimgTW いろいろ調べてみたのですね。サイモンシンがこの川の長さの下り使ってるのが意外でした。（あとで確認）四万十川は円周率越えしてました。

2019-09-01 18:37:13

流れてるこの話を遡ると、こういうところに辿り着くが、 sessendo.hatenablog.com/entry/20090504… 【『フェルマーの最終定理　ピュタゴラスに始まり、ワイルズが証明するまで』サイモン・シン／青木薫訳（新潮社、2000年）】数本試せば簡単に分かるウソをこんなにも信じられてる方が遥かに不思議で面白いと思う。 twitter.com/asunokibou/sta…

2019-09-01 13:52:05

【ケンブリッジ大学教授で地球科学者のハンス・ヘンリック・ステルムは、いろいろな川の実際の長さと、水源から河口までの直線距離との比を求めてみた。その比は川ごとに異なっていたけれども、平均すると3よりも少し大きい値になることがわかった。】注目：【川ごとに異なっていた】【平均する】

2019-09-01 13:54:10

どうも原理は蛇行絡みで、【とくにπに近くなるのは、シベリアのツンドラ地帯やブラジルのような非常になだらかな平原を流れる川の場合だ。】とのこと。すると、真っすぐで短い日本の川は大抵例外に偏ることになる。（実際にそうなってる：利根川＝322/218＝1.48） maidskii.tumblr.com/post/566613525…

2019-09-01 14:11:52

@kiruria281 @asunokibou おお、元論文までありがとうございます。シミュレーションでた、イデアな川の話なのですね。実体緩やかな川の代表例ミシシッピ川でも長さ3780km 源流から河口まで直線ざっくり2073km　比 1.8 この本の出し方は飛躍してるかなと… πは遠いですし一般化するにも遠いかな…

2019-09-01 14:30:50

アマゾン：6516÷2850＝2.29 ロシアの上位からオビ　　：5570÷2327＝2.39 エニセイ：5550÷2341＝2.37 レナ　　：4400÷2192＝2.01 アムール：4368÷2254＝1.94 一体何をどう図ったら 3.14 を割り出せるのか、逆に興味を持ってしまったぞ？

2019-09-01 15:19:10

最長支流はwikipediaの記述から割り出してるから、数百キロはズレる。しかしそれでも±0.5の精度は出せてるはず。逆に河口から長さをπ、3.0、2.5、2.0で割った同心円を書けば、厳密な源流まで遡らなくても、大外れしているのが容易に分かる。と思ってやってみたら本当に一目瞭然だった。結論：大外れ pic.twitter.com/aayeNNmI4V

2019-09-01 15:42:10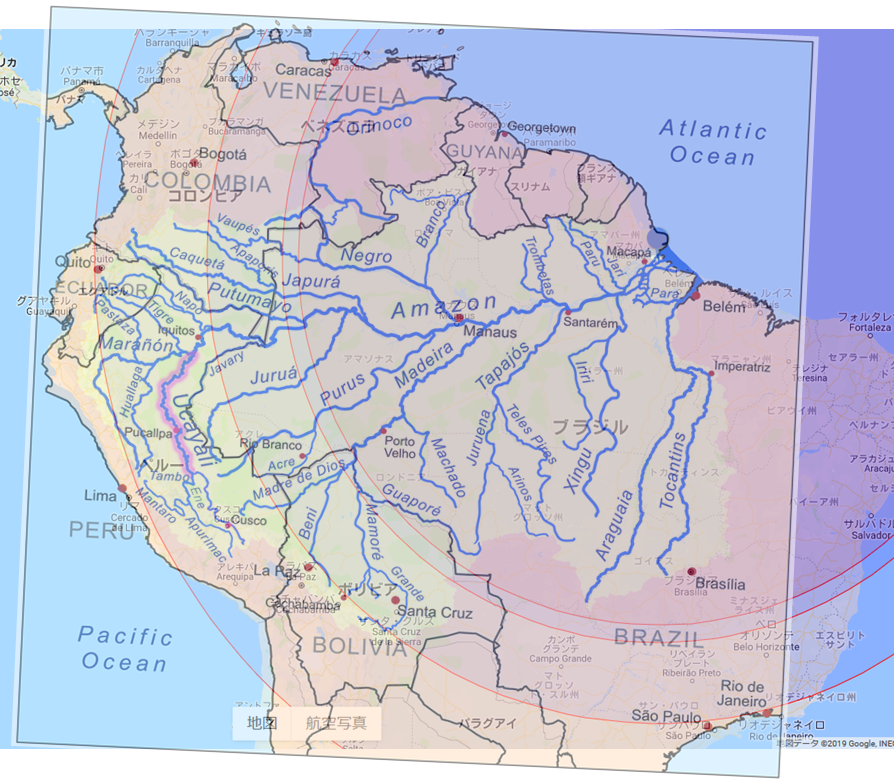

拡大

同心円を書くには multisoup 社の「同心円」を使った。 maps.multisoup.co.jp/exsample/geome… 「つくる喜び、つかう喜び」をモットーに地図で客の効率化を図る会社らしい。便利な世の中だ。感謝。アマゾン川流域図は wikipedia の図を使った。ウカヤリ川になってるのは源流調査の名残。 ja.wikipedia.org/wiki/%E3%82%A6…

2019-09-01 15:47:45

オビ川はこれ。まさか最長支流ではなくObと名乗る支流と、最大に良解釈してみたものの、残念ながら 5570km は最長支流エルティシ川（Irtysh）の値で、Obと名乗るカトゥニ川（Katun）側は 3650km しかない。どっちにしても曲直比が 3.14 には程遠い。 pic.twitter.com/B9dL5YMeh6

2019-09-01 16:02:40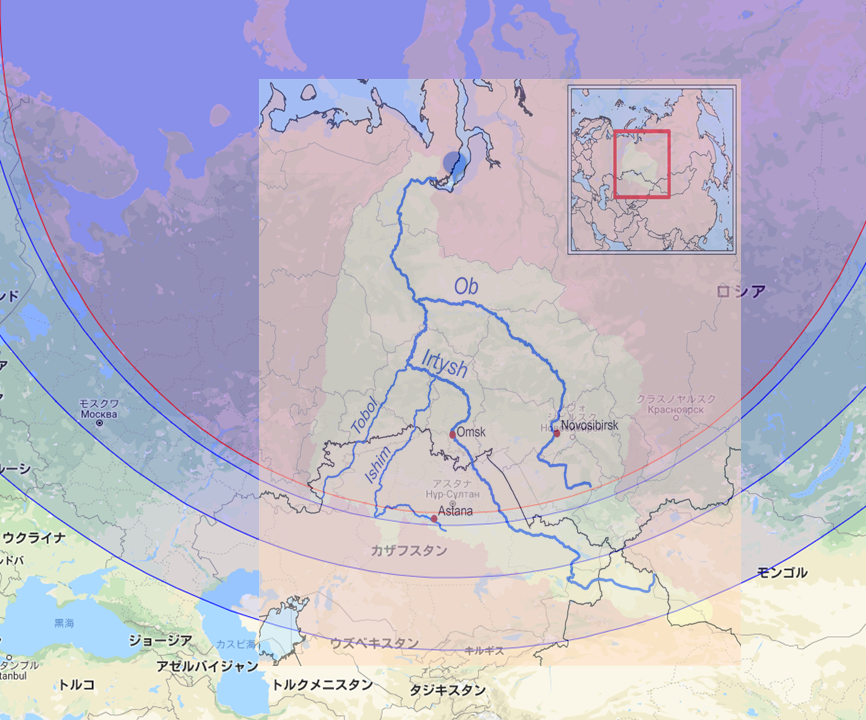

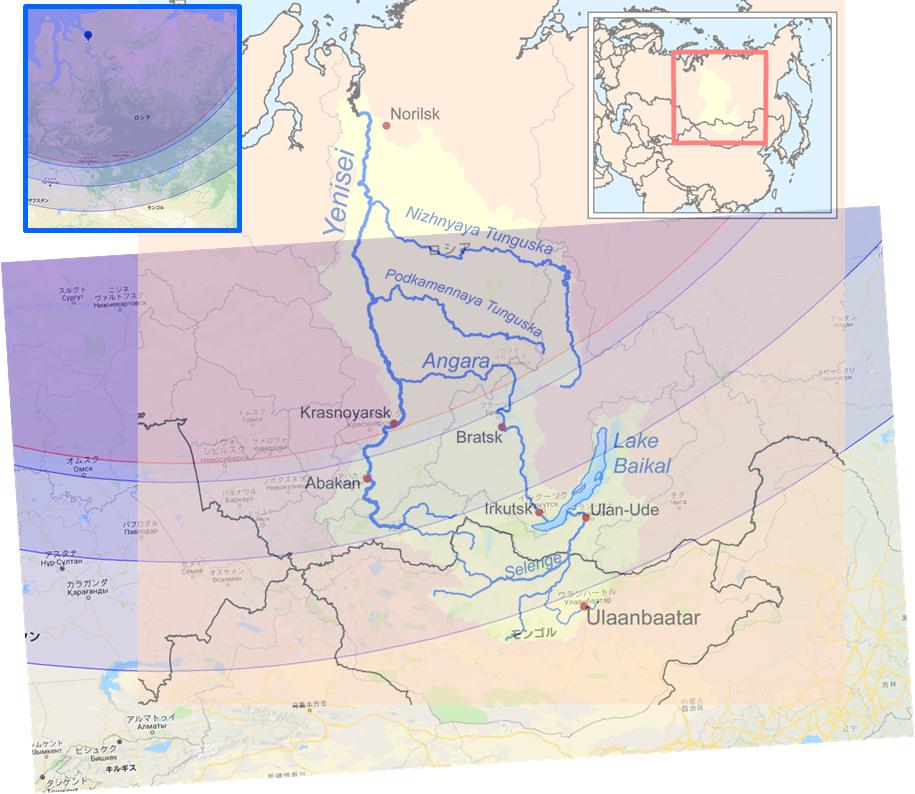拡大