-
 timekagura
timekagura
- 930
- 1
- 0
- 0
 timekagura
@timekagura
timekagura
@timekagura
空間認識の質違い 認識する為 用語(jargon)を 用意する。 座標世界 箱庭世界 日常世界 pic.twitter.com/HZZvNBBrto
2019-09-23 11:18:45 拡大
拡大
 timekagura
@timekagura
timekagura
@timekagura
座標世界は 数学の抽象性を利用する為に 細部を切り捨てた世界。 数学の自由な前提設定により 内部では整合性が整えられてる世界。
2019-09-23 11:56:41 timekagura
@timekagura
timekagura
@timekagura
原子は 陽子 中性子や 電子等の粒々が存在する 大きさ持った部分空間。 宇宙空間の部分空間に名を与え 名を与えられた部分空間内部に存在する 陽子や中性子の個数で原子の種名が、 さらに名付けられ、 区別される。
2019-09-23 11:56:49 timekagura
@timekagura
timekagura
@timekagura
だが、座標世界では 原子種別を省略し 1つの原子が この宇宙に占める空間大きさも捨象し 原子を質点同様、点扱いする。 内部空間を持たない点として 大きさ広さを持たない点として扱う。 原子の位置とか 複数原子の相互距離だけを問う。 重力や 万有引力の相互作用を考えない。
2019-09-23 11:58:24 timekagura
@timekagura
timekagura
@timekagura
数直線を頭の中でイメージし、 原子が t=0に 位置0 t=1に 位置1 t=2に 位置2 と移動するなら 等速直線運動してると 断言できる世界が 座標世界。 帰納法が適用できる。 pic.twitter.com/4W961cJH7D
2019-09-24 11:49:10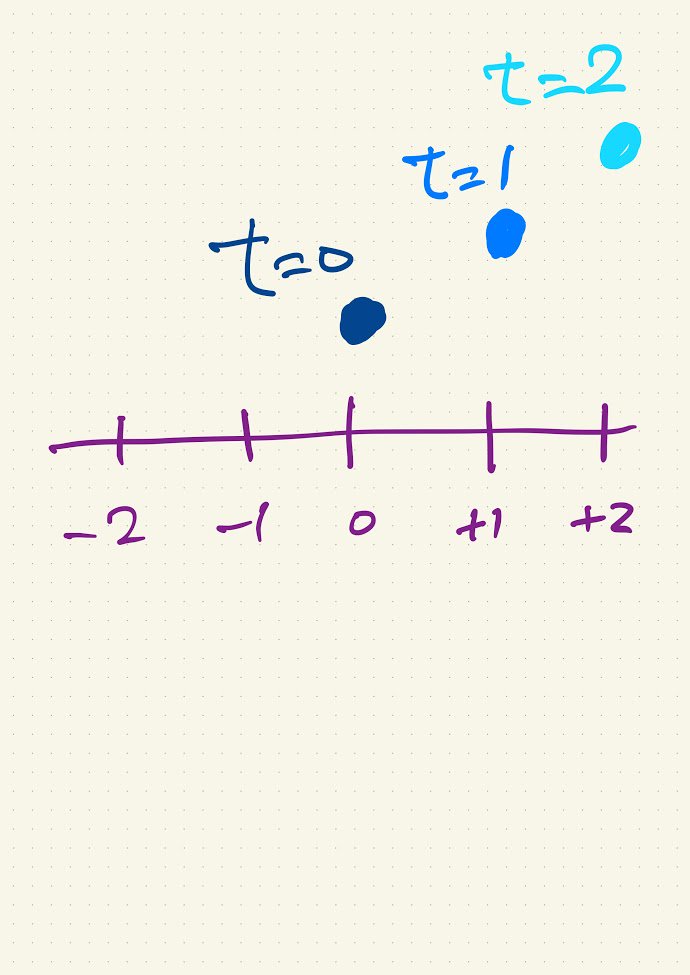 拡大
拡大
 timekagura
@timekagura
timekagura
@timekagura
ニュートンの慣性の法則も 座標世界に存在する たった1つの運動物体(原子)に 外部から力が加わらないなら いつまでも1秒毎(ごと)に 数直線上で1動く。 数直線や xy平面や xyz空間という 無限性が担保された座標空間内に 慣性の法則に従う原子1つだけ存在。
2019-09-24 11:49:53 timekagura
@timekagura
timekagura
@timekagura
でも、これって数学的思念世界。 実験で確かめるには 実験器具や定規を用意しなきゃだ。 で、実験器具や定規は原子複数の塊。 万有引力の影響が実験系に出てしまう。 つまり、慣性の法則は ガリレオ先輩のピサ斜塔実験と同じ思念的 思考実験。 測定ができない世界。
2019-09-24 11:51:35 timekagura
@timekagura
timekagura
@timekagura
ガリレオ先輩は ピサ斜塔が立つ土台、大地 地球に 鉄球1つ落としても 鉄球2つを 1塊(ひとかたまり)に落としても 影響が出ないという 相対性のない思考枠組み やっちゃってる。 地動説のガリレオ先輩でも、だ。
2019-09-24 11:51:59 timekagura
@timekagura
timekagura
@timekagura
地球を出発した光速ロケット内の兄は 歳(とし)とらならいけど 地球に残った弟は 老いると同じ。 地球の方が動かないで 光速ロケットの方が動いていると 座標に記述するには、第3者の判定が要る。
2019-09-24 11:54:02 timekagura
@timekagura
timekagura
@timekagura
ところが、西洋の1流頭脳からレベルが ちょい落ちる西洋人の頭脳が 集まりやすい 西洋が作り出した近代の物理学は 歴史的偉人級の頭脳を除いて 自分が動いてる可能性を全く思いつかない。 何に対して 自分が動いているかは、 まだ言わないよ。
2019-09-24 11:54:32 timekagura
@timekagura
timekagura
@timekagura
光線に対して、と、何度も言って説明してるけど 光子誕生痕跡慣性系の意味合い、 まだ貴殿に伝わってると 思ってないから。
2019-09-24 11:54:38 timekagura
@timekagura
timekagura
@timekagura
とにかく ニュートンは リンゴが落ちるの見て 月が地球に落ちる発想した。 このときリンゴが落ちるの見て 地球が リンゴに向かって落ちるの発想も 同時にした。 相対性の導入だ。
2019-09-24 11:55:37 timekagura
@timekagura
timekagura
@timekagura
数直線をイメージし 1秒間に1単位動く原子1個をイメージする。 数直線という 無限長さ座標空間に 他の原子存在が「居ない」。 数学者は超越者だから 宣言だけで、他の原子存在が 無限な空間内に存在しないことを定義できる。
2019-09-24 11:57:09 timekagura
@timekagura
timekagura
@timekagura
数直線でも xy直交座標でも xyz直交座標でも。 4つ以上の軸を直交させた空間を 普通の方々はイメージできないので不要。
2019-09-23 12:14:27 timekagura
@timekagura
timekagura
@timekagura
プロの方が もし、イメージできると言うなら それはどこかに、整合化できないものを押し付け 見てないだけ。 数学者はイメージではなく、 論理の整合性で やってるので、 それは構わない。
2019-09-23 12:16:23 timekagura
@timekagura
timekagura
@timekagura
視覚的イメージってのは 部分だけを見る。 扱ってる空間そのものの全体空間を見ることができない。 部分空間内に、対象物体(被写体)の 輪郭イメージを描く。
2019-09-23 12:16:52 timekagura
@timekagura
timekagura
@timekagura
それでは、「箱庭世界」では、どうだろうか。 頭の中で、実験空間の立方体をイメージする。 だが、立方体という形をイメージしただけなので、 この立方体の大きさが不明。 数学の不定とか不能に近いかな。
2019-09-23 12:21:00 timekagura
@timekagura
timekagura
@timekagura
座標空間は 等間隔の目印が 数になる世界観だけど 箱庭世界では 視野内に見えた形イメージ(輪郭線で閉じた領域)を 視野という、液晶画面枠内のドット全数に対して 輪郭線で閉じた領域のドット数の 割合比でしか 語れない世界。
2019-09-24 12:02:31 timekagura
@timekagura
timekagura
@timekagura
日常では、ヒトの身長は 1メートル。 胎児とかは別にして、 10cmということはないし、 10メートルということもないから ヒト形(がた)を 頭の中でイメージしたら 11cmから9.99メートルぐらいだと 日常で使われる単語言葉に引きずられ 思い込む。
2019-09-23 13:25:10 timekagura
@timekagura
timekagura
@timekagura
頭の中で ヒトの姿、形 輪郭をイメージしただけなのだから 大きさを宣言していない状態。 数学者なら 被写体(第1者)は 数直線上の x=5に位置してると 質点同様に、物体占有空間 大きさを点で代理させ 物体位置を宣言できるし 碁石が盤上の交点を隠すような感じ。で、位置を宣言できる。
2019-09-24 12:05:42 timekagura
@timekagura
timekagura
@timekagura
一方、視覚的イメージ重視の箱庭世界では 視野枠というチェス盤や 将棋盤の 枠複数集まりに対して 盤上の1つの枠に駒を 枠の中央ピッタシに置くというのは 設計図的理念的で 実際に駒を置くと、 枠の左上隅に近かったり 枠の右上隅でも右下隅でもない 枠内の右側に 駒が寄ってしまったりする。
2019-09-24 12:06:31 timekagura
@timekagura
timekagura
@timekagura
盤上の枠複数集まりが 視野に相当し その1つの枠に注目し、 その枠1つの空間内に駒を置き 駒の輪郭線と 駒を置いた枠が ◎二重丸の関係。 将棋盤9x9マス目 集合体や チェス盤 8x8マス目 集合体が、3重丸。 wiki pic.twitter.com/cl1cH50Ipv
2019-09-24 12:20:20 拡大
拡大
 拡大
拡大