-
- いいね！1
モト@PPMMPPP
@29silicon
正規分布から外れる理由って… 食べログ3.8問題を検証 - クイックノート clean-copy-of-onenote.hatenablog.com/entry/tabelog3…
2019-10-08 19:16:30
高橋将宜 Masayoshi Takahashi
@M123Takahashi
ヒストグラムのビンが細くて、いびつな分布に見えているだけのような気がします。観測数が1200なので、スタージェスの公式から、ビンの数は11程度が普通のヒストグラムと思われますが、この図ではビンが60以上あって、データを細切れにし過ぎていると思われます。 twitter.com/h_okumura/stat…
2019-10-09 13:56:10
高橋将宜 Masayoshi Takahashi
@M123Takahashi
以下の要領で、Rで乱数を生成してみます。R関数rnormを用いているので、x1は正規乱数です。図は次ページに示すとおりで、ヒストグラムのデフォルト設定（スタージェスの公式）を使えば（続く） set.seed(4) n<-1200 x1<-rnorm(1200,3.6,0.1) hist(x1) hist(x1,breaks=60) twitter.com/SciCafeShizuok…
2019-10-09 14:11:32
高橋将宜 Masayoshi Takahashi
@M123Takahashi
正規分布のような形状になりますが、ビンの数を60に設定すると、リンク先のウェブサイトにあるようないびつな形状の分布になりますね。つまり、食べログは不正な操作をしているのかもしれないし、単にヒストグラムの形状の問題なのかもしれないし、リンク先の分析だけでは何とも言えないですね。 pic.twitter.com/0Y9UViaBoV
2019-10-09 14:11:33
拡大
ryozo18 諸悪莫作
@ryozo18
ただこの場合は「3.6」と「3.8」という特定のスコアの比較をしたいので、スタージェスの公式にこだわるべきではないとおもうけど
2019-10-09 14:16:09
内場 崇之(Takayuki Uchiba)
@utaka233
そういえば昔こんな記事書いた。 ヒストグラム、奥が深いよ？｜Takayuki Uchiba @utaka233｜note（ノート） note.mu/utaka233/n/n79…
2019-10-09 14:25:04
OKUMURA, Akira（奥村 曉）
@AkiraOkumura
@M123Takahashi @h_okumura 4 以上に長い裾があったりするのでそんな単純な話ではなく、またその公式は一部に細かい構造を持つような分布まで含めて普遍的に適用できるものではないです。
2019-10-09 15:32:18
OKUMURA, Akira（奥村 曉）
@AkiraOkumura
何というか、これも統計の誤用だよなあ。どうやって点数をつけてるのか分からないんだから、何をしようが「検証」なんてできない。データを見なくても分かる。konkon3249.hatenablog.com/entry/2019/10/…
2019-10-11 14:29:36
☔️
@nardtree
食べログ3.6点問題、再現した。 全体の量からは大したことがないが、多くのレビューをもらう店に限定すると、偶然とは言い難いキャップが現れ始める pic.twitter.com/xG8YSZjXhp
2019-10-11 14:32:40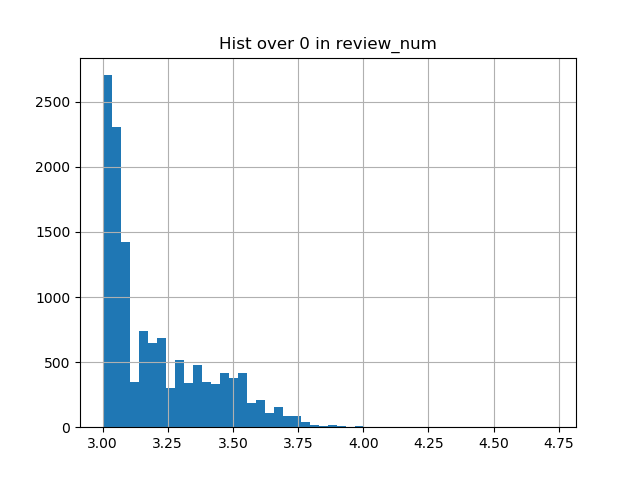
拡大
拡大
拡大
OKUMURA, Akira（奥村 曉）
@AkiraOkumura
ビン幅の設定がおかしいから変な分布になる。ビン幅をちゃんと 0.01 の倍数にしないと。こういう櫛状の分布になるときは、離散化した数値（この場合 0.01 刻み）を 0.01 の倍数じゃない幅に設定したときに必ず起きる、よくあるミス。 twitter.com/nardtree/statu…
2019-10-12 10:23:59
Kei Harada
@Seed57_cash
ちなみにもともと櫛形なんですよね。丸める前の生の値は我々にはわからないのですが。 twitter.com/AkiraOkumura/s… pic.twitter.com/pbuojdliNb
2019-10-12 12:04:08
拡大
OsciiArt◆SPNEXTcRxQ
@osciiart
@nardtree @AkiraOkumura このデータは小数点第２桁までしかない離散値です。 こういうデータのhistでbins=50みたいに指定するとbinsごとに含まれる値の種類数がバラけて偽のピークを作るのでそれを指摘されているかと。私も気になったので修正をポストしました。 gist.github.com/GINK03/8826e84…
2019-10-12 14:17:40
☔️
@nardtree
@osciiart @AkiraOkumura 色々ご意見ありがとうございます。 意見を元に修正しました。離散値なので単純に出現回数をカウントするのが良いだろうと考えて、修正したものが以下のグラフです。 pic.twitter.com/JKiwhVtBsZ
2019-10-12 15:07:05
拡大
拡大
拡大
horiem
@yellowshippo
年収の平均や中央値を聞いただけではわからん → ヒストグラムをみせろ → いやいやヒストグラムも bin 幅によって見え方が変わるぞ → スタージェスの公式というのがあってですね → いやスタージェスはサンプルサイズが 200 を超えると微妙だからフリードマン・ダイアコニスの選択を、まで予知した
2019-09-30 00:03:40
kohske
@kohske
こういう場合はヒストグラムよりもEDFで可視化したほうがいいのではないか（てきとー） twitter.com/langstat/statu…
2019-10-12 17:40:42
黒木玄 Gen Kuroki
@genkuroki
#統計 out.csvの公開どうもありがとうございます。私もグラフを描いてみました。 ビン幅(binstep)を0.01,0.02,0.05と変えて、3.0から4.0の間のみをプロット。 ヒストグラム上で、評価値3.6や3.8はそれぞれ区間 [3.6, 3.6+binstep], [3.8, 3.8+binstep] に分類されます。 twitter.com/nardtree/statu… pic.twitter.com/GXs2BtX7oj
2019-10-12 19:41:42
拡大
拡大
拡大
黒木玄 Gen Kuroki
@genkuroki
#統計 #Julia言語 のソースコードは nbviewer.jupyter.org/gist/genkuroki… で公開。 添付画像は0.01刻みでプロットした場合。 食べログ評価も0.01刻み。 3.6は区間[3.60,3.61]に分類される。 レビューの数が1以上と20以上では3.6, 3.8付近に特別な特徴は見えませんが、50以上と100以上では見える。 pic.twitter.com/CDi6T1Nbjb
2019-10-12 19:41:44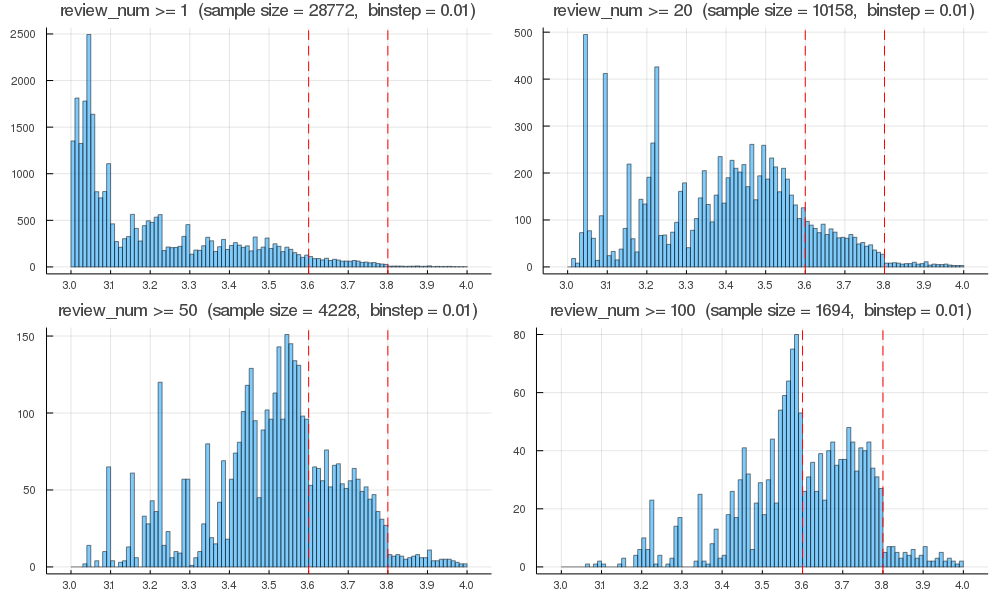
拡大
黒木玄 Gen Kuroki
@genkuroki
#統計 プロットしたデータは gist.github.com/GINK03/8826e84… 経由でダウンロード。 自分でプロットしてみた理由は、横方向の刻み幅を0.01の倍数にしたヒストグラムを見たかったから。 3.6と3.8で「異常」が見られるのはレビュー数がある程度以上多い場合をグラフに描いた場合なこともよくわかった。
2019-10-12 19:41:45
黒木玄 Gen Kuroki
@genkuroki
#統計 訂正：レビュー数が少なくても、3.8での「異常」が起こっているように見えますね。レビュー数が少ないと3.6の方の「異常」は見えない。 pic.twitter.com/yAmoEagHRq
2019-10-12 19:49:43
拡大
黒木玄 Gen Kuroki
@genkuroki
#統計 累積度数のグラフも作りました。 nbviewer.jupyter.org/gist/genkuroki… レビュー数が1,20,50,100以上の食べログ評価値の累積度数 レビュー数の制限の仕方によらずに、3.6と3.8の前後で「傾き方」が不連続に変化しているように見えます。続く pic.twitter.com/Y9mtPZG8wg
2019-10-13 10:57:01
拡大
黒木玄 Gen Kuroki
@genkuroki
#統計 レビュー数が1,20,50,100以上の食べログ評価値の累積度数のグラフを3.40～4.00に制限したもの 問題の部分を拡大してみましたが、やはり、3.60と3.80で「傾き方」が不連続に変化しているように見える。 pic.twitter.com/ccuI9KcvT5
2019-10-13 11:00:00
拡大