 Kazu SUZUKI
@kz_suzuki
Kazu SUZUKI
@kz_suzuki
直行表の良い説明に苦悶した挙句、秋山さんたちの書籍が紹介されていますね。ぼくも直交表を理解するだけでなく、説明もできるようになりたい。>> 直交表を利用すると、実験回数が少なくて済む理由 http://t.co/TRlzlSP8
2012-04-13 12:23:43 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
.@kz_suzuki 最近、使っている直交表の説明の表です。L25直交表なので5水準の因子がA列~F列まで6つあります。 http://t.co/Kq9B2FWb
2012-04-14 01:45:56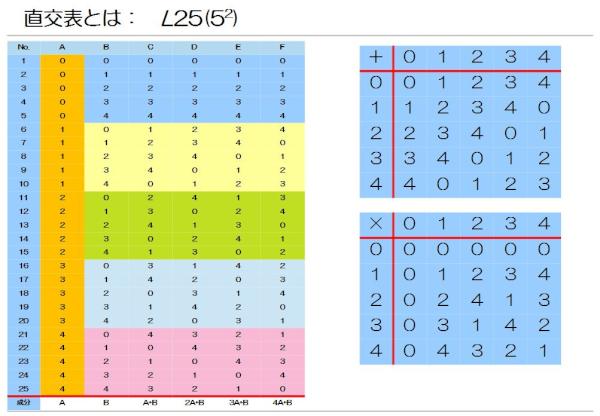 拡大
拡大
 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
まず、1行~5行のB列~F列の青色のエリアに着目してください。ここの領域で0-0、1-1、2-2、3-3、4-4、5-5といった同じ水準同士の組合せが現れています。
2012-04-14 01:48:29 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
次の黄色のところ。こちらは、それぞれの列が上に一つずつずれていますね。ここでは、青色のエリアと違って、どの行にも同じ数字がありません。ということは、青色のエリアと違った組合せが増えているってことです。
2012-04-14 01:51:08 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
真ん中の緑色のエリア。今度は、黄色のエリアと違って、それぞれの列が二つずらしになっています。ということは、ここでもまた青色・黄色と同じ組合せは一つとしてありません。
2012-04-14 01:52:52 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
同様に、水色エリアでは三つずらし、桃色エリアでは四つずらしています。五つずらしたら、、、元の青色のエリアと同じになってしまいますのでここまでです。
2012-04-14 01:54:24 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
これで、B列からF列にかけてすべての水準の組合せが現れましたね。それぞれのエリアの各列には0~4までの数値が入っているということは、それぞれのところに同じ数値をいれてやればいい。そうやってA列を増やすことが出来ます。
2012-04-14 01:56:06 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
でも、5水準の直交表なら手間もさほどかからないけど、17水準とかになったら17行ずつのエリアで一つずつずらし方を増やしながら表を作るのは面倒で間違えやすいですね。
2012-04-14 01:58:35 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
だから、算数を使います。一番下の成分って行がそれ。A列とB列から計算でC列~F列を作っちゃおうというわけ。17水準でも一緒。A列とB列からC列~Q列を作ることが出来ます。
2012-04-14 02:00:50 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
まず、A列とB列はいいよね。ただの総当たりです。C列を作る時にはC列の一番下の成分に「A+B」って書いてあるから足し算をしてあげるだけです。
2012-04-14 02:02:18 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
ただし、普通に足し算してしまうと、3+4=7なんて数値が出てきてしまうから右の表を使うのです。これは、(A+B) mod 5、つまりAとBを足したものを5で割った余りの表になっています。5進数1桁の足し算って考えてもいいよ。
2012-04-14 02:04:14 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
この計算、ちょっと変わっているルールだけど、四則演算が普通に成り立つから「体」っていうんだ。そして、演算結果が0~4の5つしかない、つまり、有限の数しかないので有限体っていう名前が付いてるよ。
2012-04-14 02:08:39 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
この例は5水準系直交表(L25)だったけど、全く同じ作り方で2水準系直交表、3水準系直交表、7水準系直交表、11水準系直交表、13水準系直交表、17水準系直交表、、、が作れるよ。
2012-04-14 02:11:53 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
2 · 3 · 5 · 7 · 11 · 13 · 17 · 19 · 23 · 29 · 31 · 37 · 41 · 43 · 47 · 53 · 59 · 61 · 67 · 71 · 73 · 79 · 83 · 89 · 97 …… 水準系直交表がこの方法で作れるんだ。
2012-04-14 02:14:00 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
気が付いたよね。これらの数値はみな素数になっています。素数系直交表はみんなA, B, A+B, 2A+B, 3A+B,...を「水準数+1」列まで作ってやればいい。
2012-04-14 02:16:36 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
じゃあ、L36(6^2)は6が素数じゃないから作れないのかって? 実は数学的な証明はされていないけど、たぶん、できないって言われてる。少なくとも、小さなL36ではコンピュータで計算して不可能であることが確認されてるんだって。
2012-04-14 02:18:56 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
えーホントかなぁ? と疑りぶかいあなたのために、L16(4^2)を同じ方法で作ってみたよ。 http://t.co/natjUs57
2012-04-14 02:22:49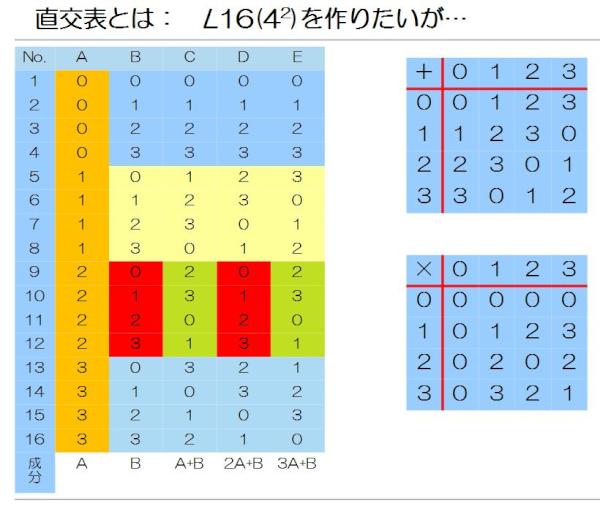 拡大
拡大
 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
上から3段目の、つまりは二つずらしのところで、青色エリアで出現済みの同じ水準同士の組合せがでてるでしょ。ということは、BとDで言えば、0-1とか現れていないってこと。
2012-04-14 02:25:21 Kazu SUZUKI
@kz_suzuki
Kazu SUZUKI
@kz_suzuki
ああ、紙と鉛筆‥、いやExcelが欲しい‥。春の夜長の全日空ホテル‥。ソフトウェアテスト入門では、直交表の説明にxorが出てきた気がします。何となく対称性に欠けている気がした。理解が及んでいない。
2012-04-14 02:25:36 あきやま🍠
@akiyama924
あきやま🍠
@akiyama924
なんで、3段目で同じ組合せが現れたかというと、右下の掛け算の表を見てもらうとわかるんだけど、「2×1=2」「2×3=2」とどちらも同じ結果になってしまってるでしょ。こういうのって四則演算が成り立っていないっていうんだ。
2012-04-14 02:31:13