素人の考察～放射性物質：崩壊確率と半減期の関係（近似式）
-
iamdreamers
- 5633
- 0
- 0
- 0
-
- いいね！0
まえがき
放射性物質と半減期
夢乃
@iamdreamers
放射性物質は、決まった時間、決まった確率（放射性物質の種類により異なる）で、放射線を出して崩壊し別の物質になる。時間が長くなれば、崩壊する確率も高くなる。この確率が50%になる時間を半減期という。
2012-12-08 09:10:50
夢乃
@iamdreamers
原子一個に着目すると、「半減期の間に放射線を出して崩壊する確率が50%」ということであり、多数、例えば原子十億個に着目すると、「半減期の間に約半分の五億個の原子が放射線を出して崩壊する」ということになる。
2012-12-08 09:11:13
夢乃
@iamdreamers
前述の通り、原子によって一定時間の間に崩壊する確率は決まっているので、この確率がわかれば半減期も計算できる、はず。これを計算してみよう。
2012-12-08 09:11:51崩壊確率の計算式を求める・その１
夢乃
@iamdreamers
ある放射性物質が一定時間、面倒なので１秒間として、１秒間に崩壊する確率をｐ（０＜ｐ＜１）とする。この物質がｎ秒間に崩壊する確率をＦ(ｎ)として、Ｆ(ｎ)を表す式を考える。
2012-12-08 09:12:16
夢乃
@iamdreamers
０秒間に崩壊する確率Ｆ(０)＝０。時間が経過しなければ崩壊しようがないので当たり前。 http://t.co/4lwtKRd6
2012-12-08 09:13:09
拡大
夢乃
@iamdreamers
１秒間に崩壊する確率Ｆ(１)＝ｐ。１秒間に崩壊する確率がｐの放射性物質を想定しているので、これも当たり前。 http://t.co/3vKzoWP3
2012-12-08 09:13:50
拡大
夢乃
@iamdreamers
２秒間に崩壊する確率Ｆ(２)は、２ｐじゃない（ここから少し面倒臭い）。２秒間に崩壊する確率とは、「最初の１秒間で崩壊する確率」（＝Ｆ(１)）と、「最初の１秒間で崩壊せず、かつ、次の１秒間で崩壊する確率」の合計になる。
2012-12-08 09:14:25
夢乃
@iamdreamers
「最初の１秒間で崩壊しない確率」は１－ｐ、「次の１秒間で崩壊する確率はｐ」なので、これらを纏めると、Ｆ(２)＝Ｆ(１)＋ｐ(１－ｐ) となる。 http://t.co/JgH1P2Tf
2012-12-08 09:14:56
拡大
夢乃
@iamdreamers
３秒間に崩壊する確率Ｆ(３)も同じく、「最初の２秒間に崩壊する確率」と「最初の２秒間で崩壊せず、次の１秒間で崩壊する確率」の合計なので、Ｆ(３)＝Ｆ(２)＋ｐ(１－ｐ)＾２ になる。 http://t.co/zRzliCbd
2012-12-08 09:15:49
拡大
夢乃
@iamdreamers
ここまでくれば、ｎ秒間に崩壊する確率Ｆ(ｎ)もわかる。「最初の(ｎ－１)秒間に崩壊する確率」と、「最初の(ｎ－１)秒間に崩壊せず、次の１秒間で崩壊する確率」の合計なので、Ｆ(ｎ)＝Ｆ(ｎ－１)＋ｐ(１－ｐ)＾(ｎ－１) になる。 http://t.co/DiSrDskV
2012-12-08 09:16:44
拡大
夢乃
@iamdreamers
ここで、ｆ(ｎ)＝ｐ(１－ｐ)＾(ｎ－１) とすると、Ｆ(ｎ)＝Σｆ(ｉ) （ｉ＝１～ｎの合計）と表せる（正しい表記は図を見てっ）。これを計算すると、Ｆ(ｎ)＝１－(１－ｐ)＾ｎ と単純化できる。 http://t.co/ihhmVJA0
2012-12-08 09:17:30
拡大
崩壊確率の計算式を求める・その２
夢乃
@iamdreamers
１秒間に崩壊する確率Ｆ(１)は、「１」（100％）から「１秒間に崩壊しない確率」を引いた値とも表せる。ということは、Ｆ(１)＝１－(１－ｐ) になる。 http://t.co/OFVuqfIg
2012-12-08 09:18:50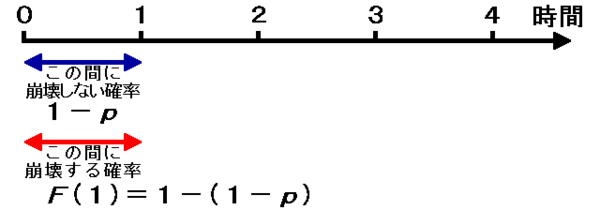
拡大
夢乃
@iamdreamers
２秒間に崩壊する確率Ｆ(２)は、「１」（100％）から「２秒間に崩壊しない確率」を引いた値なので、Ｆ(２)＝１－(１－ｐ)＾２ になる。 http://t.co/lNzWgDXm
2012-12-08 09:19:33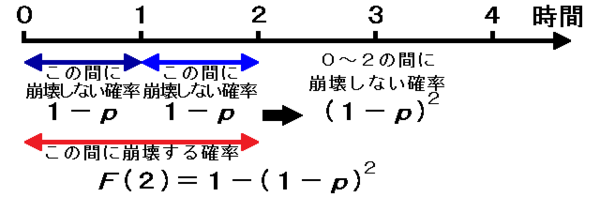
拡大
夢乃
@iamdreamers
３秒間に崩壊する確率Ｆ(３)は、「１」（100％）から「３秒間に崩壊しない確率」を引いた値なので、Ｆ(３)＝１－(１－ｐ)＾３ になる。 http://t.co/8bO9KtNx
2012-12-08 09:20:17
拡大
夢乃
@iamdreamers
同じように考えていくと、ｎ秒間に崩壊する確率Ｆ(ｎ)は、「１」（100％）から「ｎ秒間に崩壊しない確率」を引いた値なので、Ｆ(ｎ)＝１－(１－ｐ)＾ｎ になる。つまり、さっきの式と同じ。 http://t.co/cf1oCLxj
2012-12-08 09:21:00
拡大
一定時間での崩壊確率と半減期の関係
夢乃
@iamdreamers
今度は、１秒間に崩壊する確率ｐと半減期の関係は、というと・・・半減期とは「放射性物質の崩壊する確率が50％になる時間」なので、さっき求めた式に当てはめて、０.５＝１－(１－ｐ)＾ｎ を満たすｎが半減期、ということ。 http://t.co/2R4LDiTh
2012-12-08 09:21:54
拡大
夢乃
@iamdreamers
これをｎについて解くと、ｎ＝－１÷(log(１－ｐ,２)) となり、これが一定時間に崩壊する確率ｐから半減期ｎを計算する式（正しい表記は図を見てっ）。 http://t.co/kZciHejf
2012-12-08 09:22:44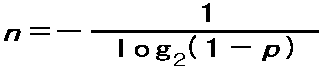
拡大
夢乃
@iamdreamers
ついでに同じ式をｐについて解くと、ｐ＝１－１÷ｎ√２ となり、これが半減期ｎから一定時間に崩壊する確率ｐを計算する式（これも正しい表記は図を見てっ）。 http://t.co/YK5ek1qk
2012-12-08 09:23:27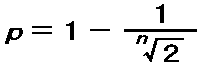
拡大