
『低線量被曝と統計的有意』東京GIGOさんのツイートまとめ(2014.4.7作成) ♯LNT仮説 ♯LNTモデル
-
 uchida_kawasaki
uchida_kawasaki
- 4294
- 1
- 0
- 6
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
元々かかる何らかの病気があったとして、別の要因によりそれが増加したとする。その増加がわずかであれば誤差の範囲で起きた偶然だろうし、増加が大きければ誤差の範囲や偶然とは言えなくなる。
2014-04-06 23:32:37 東京GIGO
@ekb90377
東京GIGO
@ekb90377
標本の大きさ10万人で考えてみる。元々1%がかかる病気の場合、罹患数は1,000人となるが、それがどのくらい増えると『統計的有意(p<0.05)』になるだろうか?
2014-04-06 23:33:14 東京GIGO
@ekb90377
東京GIGO
@ekb90377
χ2検定による計算結果。10万人あたり1,000人の罹患数に対して、90人以上増加すると『統計的有意(p<0.05)』になる。 http://t.co/4yjcRih5hm
2014-04-06 23:34:16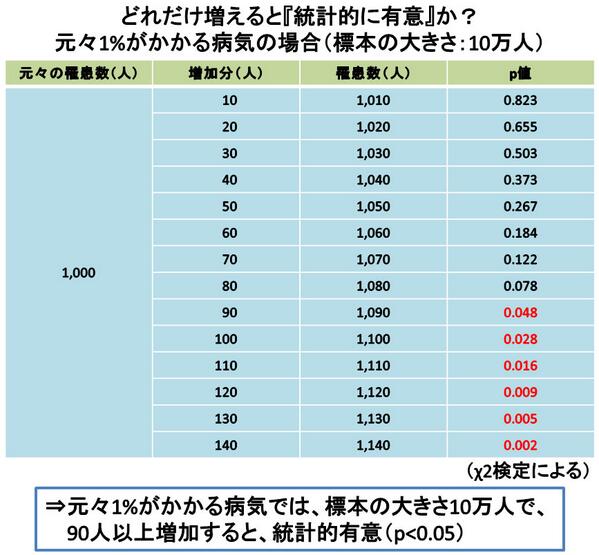 拡大
拡大
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
次に、元々30%がかかる病気で考えてみる。この場合は、10万人あたり30,000人の罹患数に対して450人以上増加すると『統計的有意(p<0.05)』になる。元々の罹患率(バックグラウンド)が大きくなるほど、増加の検出が難くなる。 http://t.co/byZNVjBWrD
2014-04-06 23:36:29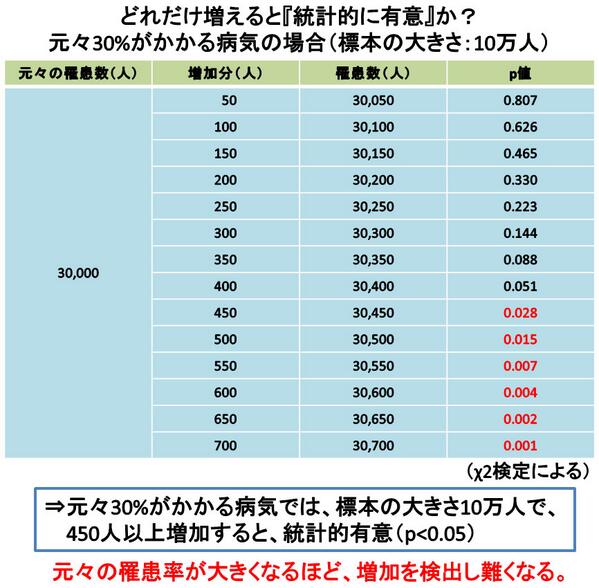 拡大
拡大
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
自然ガン死率(被曝と関係なく、生涯にガンで死ぬ率)を30%とした場合。標本の大きさと被曝量に対するp値は、このようになる。 http://t.co/0FKB76omE3
2014-04-06 23:38:04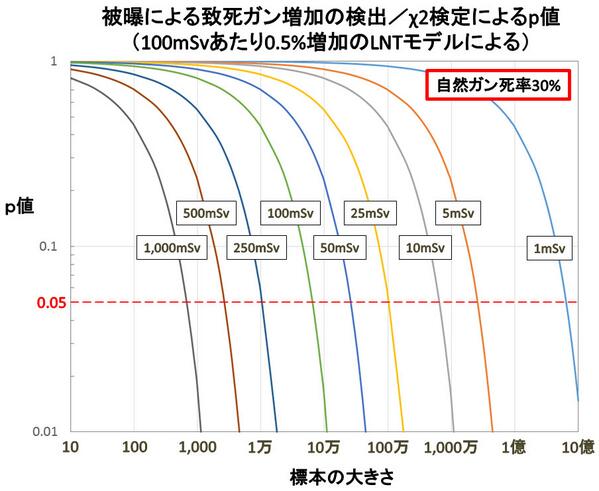 拡大
拡大
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
自然ガン死率を1%とした場合。標本の大きさと被曝量に対するp値は、このようになる。 http://t.co/1pRwRsF57i
2014-04-06 23:38:47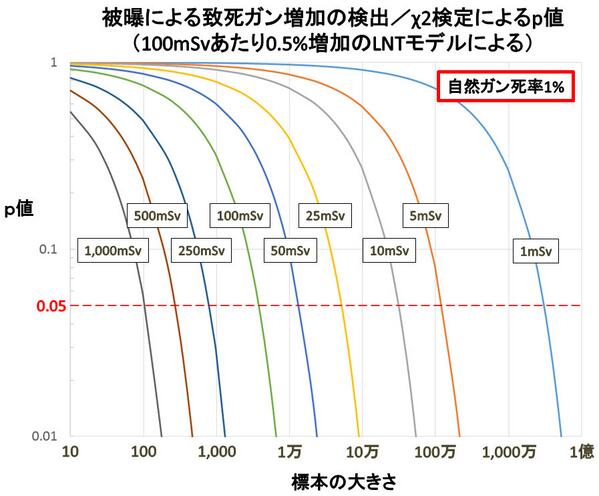 拡大
拡大
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
これらを表にしたもの。『被曝による致死ガン増加をχ2検定により有意水準5%で検出するのに必要な標本の大きさ』。 http://t.co/ApfB1GRe6a
2014-04-06 23:39:27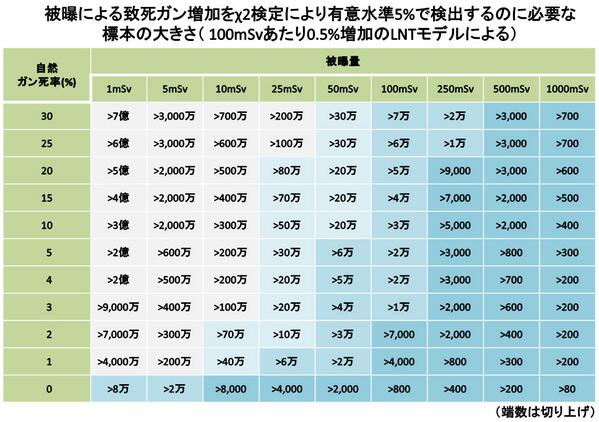 拡大
拡大
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
わが国の自然ガン死率は概ね20%~30%前後であろうが、その付近で100mSvのところを見てみると、必要な標本の大きさは数万。他方、50mSvのところを見てみると、必要な標本の大きさは数十万となる。
2014-04-06 23:40:30 東京GIGO
@ekb90377
東京GIGO
@ekb90377
ヒロシマ・ナガサキの事例で、100mSvより小さな低線量被曝の領域で、統計的な有意(p<0.05)が確認されなかったのは、このような、標本の大きさの限界によるものであろう。
2014-04-06 23:41:08 東京GIGO
@ekb90377
東京GIGO
@ekb90377
国立がん研究センターがん対策情報センター『人口動態統計によるがん死亡データ(1958年~2012年)』より、2012年の自然ガン死率(累積値)をグラフにしたもの。縦軸は対数である。加齢とともにガン死率は急激に増加する。 http://t.co/zDVmFmz6r5
2014-04-06 23:42:23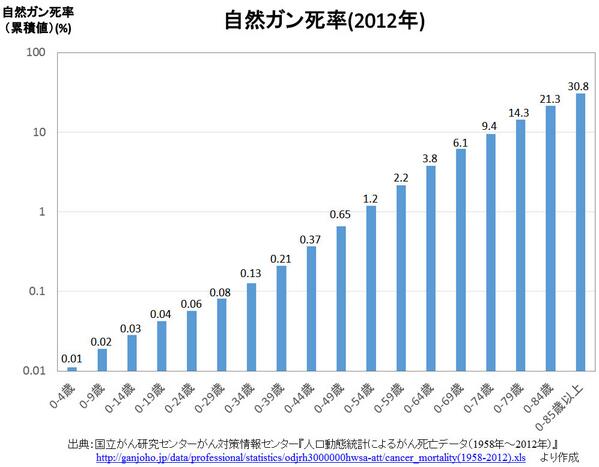 拡大
拡大
 東京GIGO
@ekb90377
東京GIGO
@ekb90377
よく言われる(日本人の3割以上がガンで死ぬ)というのは、確かにその通りだが、それは85歳以上までカウントした場合の話。0-74歳では9.4%、0-69歳では6.1%、0-59歳では2.2%のように、年代が若くなれば高々数%のオーダーである。
2014-04-06 23:43:13 東京GIGO
@ekb90377
東京GIGO
@ekb90377
つまり、被曝による過剰な致死ガンの発生をカウントする際に、全生涯でカウントすると30%以上のバックグラウンドと比較することになるが、カウントする範囲が若い年齢までであれば、それよりもずっと小さいバックグラウンドと比較することになる。
2014-04-06 23:43:55 東京GIGO
@ekb90377
東京GIGO
@ekb90377
例えば、現実に起り得そうなケースとして、子供や若者が、年2.5mSvの過剰被曝を10年続けると、累計25mSvとなる。(子供の場合は放射線感受性の係数をかける必要があるが、とりあえずここでは考えないこととする)
2014-04-06 23:45:16 東京GIGO
@ekb90377
東京GIGO
@ekb90377
この影響による過剰致死ガンが、LNTモデルに従って発生するとして、その多くが79歳までに発生するとすれば、検出に必要な標本の大きさは<70万。69歳までに発生すれば<50万、64歳では<20万、54歳では<10万、49歳では<6万である。
2014-04-06 23:45:54 東京GIGO
@ekb90377
東京GIGO
@ekb90377
結論。(100mSvより小さな低線量被曝による過剰な致死ガンの発生は、統計的に検出できない)これはあくまで、ヒロシマ・ナガサキ事例での話。
2014-04-06 23:46:22 東京GIGO
@ekb90377
東京GIGO
@ekb90377
子供や若者の被曝(例えば累計25mSv程度)による過剰な致死ガンの多くが、もし老年期以前に発生した場合には、数十万~数万の標本の大きさでも統計的有意(p<0.05)で検出され得る。
2014-04-06 23:47:05 東京GIGO
@ekb90377
東京GIGO
@ekb90377
以下余談。(低線量被曝でのLNTモデルには統計的有意はない。だから低線量被曝には閾値があって、それ以下では被曝の影響はほとんどない)というのは、考え方としておかしい。
2014-04-06 23:47:40 東京GIGO
@ekb90377
東京GIGO
@ekb90377
例えば100mSvに閾値があって、それ以下ではLNTで計算される値の1/10になるとする。この『LNT×1/10モデル』は、統計的有意という観点からは、LNTモデルよりもはるかに遠くにある。
2014-04-06 23:48:21 東京GIGO
@ekb90377
東京GIGO
@ekb90377
なぜなら、LNT×1/10モデルの50mSvにおける統計的有意を得るには、LNTモデルの5mSvの統計的有意を得るのと、同じ標本の大きさが必要となるからである。
2014-04-06 23:48:49 東京GIGO
@ekb90377
東京GIGO
@ekb90377
(有意は確認されたけども、その効果(傾き)は、LNTで計算されるものよりも、ずっと小さかった)統計的にこれを確かめるのは、LNTモデルを確かめるよりも、はるかに至難のわざなのである。
2014-04-06 23:49:55