相関係数の大小は相関の有無とは全く関係ない件について。
-
- いいね！233
発端となったのはこのツイート
Masa Kotosaka (琴坂将広)
@kotosaka
悪いことは言わない。この分析をした人、私が良い事（分析の基本）を教えてあげるので、大人しく出て来て下さい。いや、ほんとお願いです（哀）→ 出典 2014年10月29日日経新聞朝刊総合１「地方創生「東京集中是正論」の裏側 pic.twitter.com/yXUuybF787
2014-10-29 14:28:35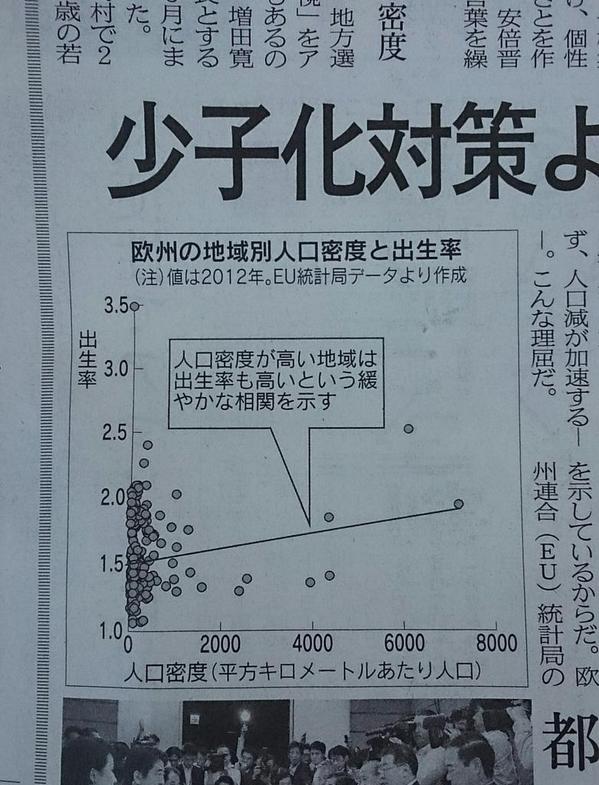
拡大
それに対するTwitterでの反響
しーたけ
@shi_taken
勢いと雰囲気で押し切るトンデモグラフを堂々と掲載してきた日経新聞 - Togetterまとめ togetter.com/li/738694 このまとめを見て驚くのは「相関係数が大きければ相関があり、小さければない」という勘違いの多さ。相関係数の大小と相関の有無は全く関係がない。
2014-11-01 07:27:02相関係数の意味と、相関の有無を判定する方法について
しーたけ
@shi_taken
相関係数が示すのは、xとyが相関しているという前提の下、yの値を決定するのにxがどれだけ寄与しているかという「寄与率」。x以外にもyに影響する因子があれば小さく、なければ大きくなるというだけの話。さらに言えば、相関しているという前提が間違っていたら話にならない。
2014-11-01 07:29:06
しーたけ
@shi_taken
例えばプロットが2つしかなければ、相関の有無に関わらず相関係数は必ず1か-1になるが、これを相関があるという人はいない。(相関がないということではなく、データ数が小さすぎて相関の有無を判定できないということ。)
2014-11-01 07:30:37プロットが2つしかなければ、当然こうなります。
しーたけ
@shi_taken
相関の有無を判定するのに使われるのは、相関係数rとプロット数nによって決定される"p値"で、相関があるという前提が正しくない確率を示す。正確には、「全く相関していないxとyをアトランダムにn個プロットしたグラフの相関係数を算出したとき、それがrになる確率」を示す。
2014-11-01 07:31:53
しーたけ
@shi_taken
一般的にはp<0.05のとき「(有意水準5％で)有意な相関がある」という。先述したプロット数が2つの場合では、相関係数は1と高くなるが、p=1となるためこれは有意な相関ではない。
2014-11-01 07:33:16
しーたけ
@shi_taken
逆に相関係数が小さくてもプロット数が十分に多ければp<0.05になることはある。この場合、xとyの間には有意な相関があるが、寄与率は小さく、x以外の因子がより強くyに影響しているという意味になる。
2014-11-01 07:34:24
しーたけ
@shi_taken
p値の考え方について例えてみる。全くイカサマのないコインを投げて6回連続で同じ面が出る確率は3.1％で、5％より小さい。したがって、ある人がコインを投げて6回連続で同じ面が出た時には、「これはイカサマではないか？」という疑いが妥当性を持つと考える。この3.1％に相当するのがp値。
2014-11-01 07:35:25
しーたけ
@shi_taken
相関係数至上主義というか、p値が軽視されがちなのは、おそらくExcelでは相関係数は簡単に出せるがp値を出すのには手間がかかるせいだと思う。統計解析にはExcelではなくRやSPSSなどのちゃんとした統計ソフトを使ってほしい。
2014-11-01 07:36:19おまけ。パラメトリック手法とノンパラメトリック手法について
しーたけ
@shi_taken
また、相関解析にはパラメトリック手法とノンパラメトリック手法の2通りがあることにも注意されたい。Excelで算出されるpearsonの相関係数は前者だが、環境科学や社会科学ではほとんどの場合後者の方が適切。
2014-11-01 07:37:34
しーたけ
@shi_taken
パラメトリック手法はデータが正規分布やt分布など特定の分布に従うことを前提としている。そのため、こういった分布に従わないデータでは外れ値に引っぱられて不正確な値が出やすい。
2014-11-01 07:38:29
しーたけ
@shi_taken
ノンパラメトリック手法は分布のしかたに関わらず使うことができ、外れ値に強い。一方で有意であると判定する(p<0.05になる)のに必要なデータ数がパラメトリック手法と比較して多くなるという短所もある。
2014-11-01 07:39:57
しーたけ
@shi_taken
環境中における物質の動態や、社会における人の行動などは、影響する因子があまりに多く複雑であるため、ほとんどの場合特定の分布に従わない。したがってノンパラメトリック手法であるspearmanの順位相関係数が推奨される。
2014-11-01 07:41:39実際に計算してみた
しーたけ
@shi_taken
奥村先生のサイトに上げられた日経のグラフの元データを使って統計ソフトRで相関検定をしてみた。 oku.edu.mie-u.ac.jp/~okumura/stat/…
2014-11-01 07:47:52
しーたけ
@shi_taken
Pearsonの相関係数r=0.045 (p=0.47)となり、有意な相関はない。一方でSpearmanの順位相関係数r=-0.14 (p=0.025) となり、なんと有意な負の相関が認められた。
2014-11-01 07:48:28
しーたけ
@shi_taken
奥村先生のサイトに貼られた日経のものと同じグラフ(左図)、その横軸を対数目盛にしたグラフ(右図)を見比べてみる。 pic.twitter.com/rOQ4X3BTcg
2014-11-01 07:53:42
拡大