誰も解けない図形問題…結論出ました！

ひげお @Higeow

【拡散希望】斜線の部分の面積を求める問題です。中学の知識で解ける……とのことなのですが、解けません！解けたら解法教えて下さい！ pic.twitter.com/iUi4OYA5MP

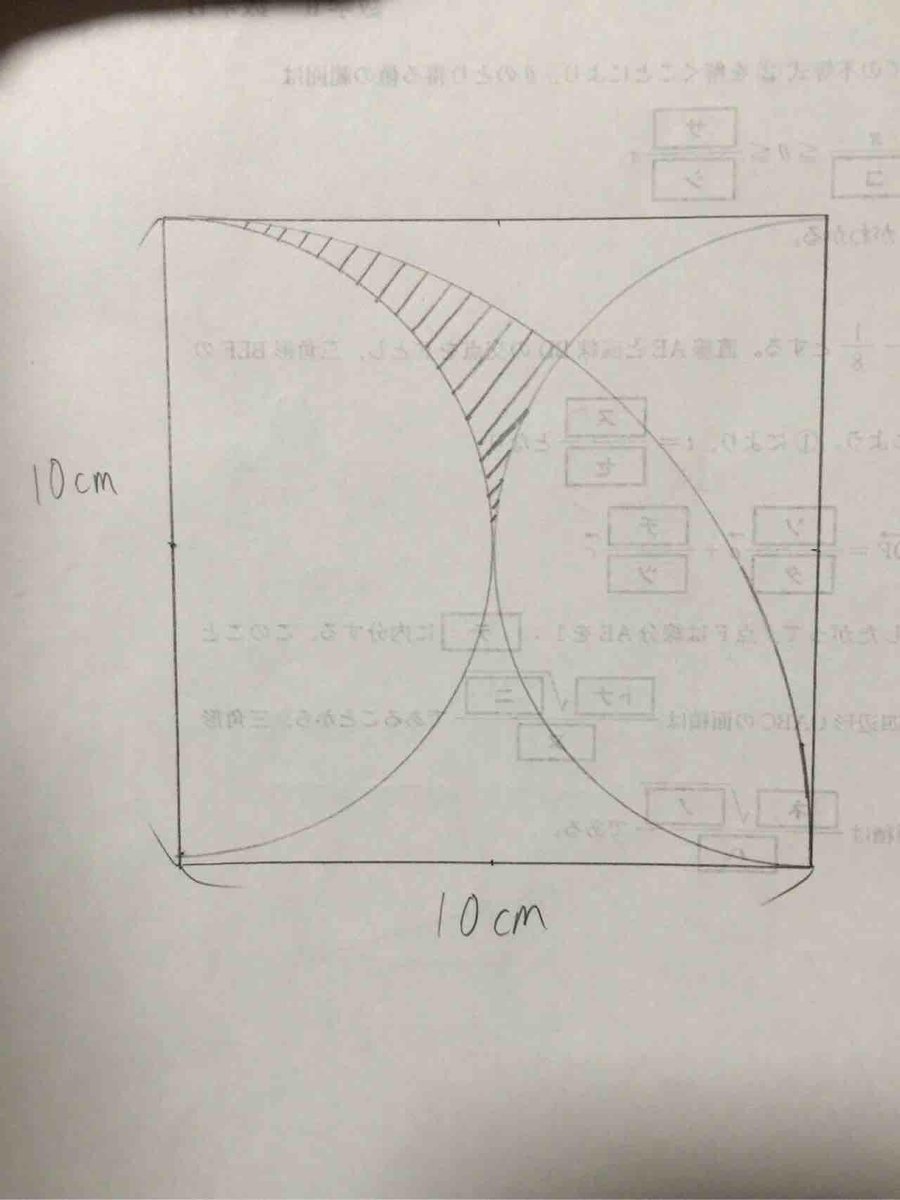拡大

ひげお @Higeow

できればできそうな人のところまで回してくださらんか！？今の問題かなり悩んでるんだよな

ひげお @Higeow

数学得意な人マジ頼むし。

ひげお @Higeow

マジでさっきの問題誰か数学得意な人といてくれ

ひげお @Higeow

誰かが解いて解法を教えてくれたらさも自分が解いたようにドヤ顔する準備はできてるんだ！！！

ひげお @Higeow

あ、まってできるかも

ひげお @Higeow

軽率なこと言ったわ

ひげお @Higeow

悔しくて積分で解こうとした人の話はやめよう。

ひげお @Higeow

このツイート拡散希望です。。。できるだけ多くの人からヒントをもらいたいです。チャレンジしなくてもＲＴだけでもありがたいです。 twitter.com/Higeow/status/…

ひげお @Higeow

うぉおおおおおおおおお！！！！ぜんぜん違うけどできたかもしれん！！　#なおこの数分後には

ひげお @Higeow

できませんでした。　#できなかった

ひげお @Higeow

ごめん。

ぱすてる。 @Tell_pass

@Higeow フォロー外からすいません、 こんな感じで3つの面積を分けて考えてみたらどうでしょうか？ 自分もちゃんと解いてるわけでも、答えを知ってるわけでも無いのですが、 かんがえてる途中なら申し訳ないです… :(´◦ω◦｀):！ pic.twitter.com/d3Zd5DkZvN

拡大

ひげお @Higeow

@Anthracene_ この問題の亜種というか、一番単純なやつはそういう風に図形を切り貼りして重なった部分を考えて～とかやるんですよね…。中学数学でそういう問題があって、それの難しいバージョンだと思うのですが…いかんせん解けないのです。ありがとうございます！

ぱすてる。 @Tell_pass

@Higeow うおお、そうなのですか… こんな気がしたのですが…これなら出せるぜい(੭ु˙꒳​˙)੭ु⁾⁾！なんて思ってしまった…(白目) えっと、お勉強がんばってくださいです (私も答え気になったので答え出たら知りたいですねw pic.twitter.com/i0tHYcY7qL

拡大

ひげお @Higeow

@Anthracene_ 協力ありがとうございます！僕も2行目？の図形まではすんなりいけるんですがそこから最後までがどうしても行きつけません…。答え気になりますよね…ありがとうございます！

ひげお @Higeow

これとこれとこれとこれとこれのどれかが出れば全部わかるのにどれも出ない。

ひげお @Higeow

右上のグジャァってなってる部分の一つでもわかれば、あとは連鎖的に出るはずなんだが…

ひげお @Higeow

連立するわ

ひげお @Higeow

連立建てたのに明らかにおかしい…なぜだ…！

ひげお @Higeow

建てたわ…だけだわからないところが全部で４つなのに、式が3つしかたたぬ…！

ひげお @Higeow

あ、４つめあった！

宮塚恵一@自由 @miyaduka

@Higeow たぶんおんなじことやってる、無理だ。とりあえずわたしは作業に戻ります……答えがわかったら……教えて……くれ……

kuri🍉 @kurikuri_kuriko

@Higeow 同じ図形を鏡にうつしたように左側につけたら、分かります。

ひげお @Higeow

@kurimotoatsuko うう…わかりません…。図形というのはこの図形全体でしょうか？それとも斜線部のみ？鏡写しにするのは上下でしょうか？それとも左右でしょうか？