
【ガチ学習シリーズ】数学の勉強をやり直したい人に贈る~~「どうしても理解できません」への対処
-
 beautyplanets
beautyplanets
- 20116
- 0
- 5
- 6
 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
【問題へのアプローチ①】 数学の勉強をやり直したい人向けのコラムその2です。後編を書こうと前回の内容を振り返って、ちょっとどころではない量の「書き足したいこと」があるので、今回も「苦手であまり成績が良くなかったけど、やりなおしたい」人向けの内容となります。
2015-08-22 21:02:05 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
従って「そこそこ成績取れてたけど、やり直したい」人向けは次回に回します。すみません。ただし、今回の内容は汎用性が高いので、それなりに役に立つ内容なのではないかと考えています。
2015-08-22 21:02:21 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
教科書の重要性については、これまでに何度も触れてきた通りです。その教科書の使い方についてもう少し踏み込んでおきます。これまで、無数に質問され、またコメント他でも散見されたことから解説します。
2015-08-22 21:02:44 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
以前から気になっていたのが「教科書を読んでもわからなかった」「解答・解説を読んでもわからなかった」という質問・発言です。「どこがわからないの?」と聞き返すと「全部」と返ってくるケースが殆どですが、原因ははっきりしています。
2015-08-22 21:03:16 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
大別すると原因は2つあり、1つは「前提事項が頭に入っていないために、何を書いてあるのか理解できない」ケースです。これはもう、分からない語句や概念を特定し、それを解説している箇所まで遡るしかありません。
2015-08-22 21:03:28 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
状況によっては学年を越える必要があります。積み残しですから仕方ありません。恥ずかしいだの何だのといった理由(特に思春期の場合は)で、小学校履修範囲がわからないと口に出して言うのは困難です。しかし、実際にわかっていないのですから、仕方ありません。
2015-08-22 21:03:57 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
なんとなく」「ごまかし」ていると、どんどん分からないことは積み上がっていきます。記憶力で押し切ってしまうことも可能と言えば可能なのですが、覚える能力がどこで飽和するかわかりません。対処限界を越えたところでアウトです。大半の人はコレ。
2015-08-22 21:04:16 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
対処方法は非常に簡単で、何度も言っているとおり「たとえそれが小学校1年生の履修範囲であろうと、分からないところまで遡って」理解し、そこから取りこぼしを拾いながら実学年(あるいは必要とするところまで)まで積み上げ直せば良いのです。
2015-08-22 21:04:35 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
時間がかかるではないか!と思うかも知れませんが、そこは安心しましょう。成長するに従って理解力そのものは高まっているので、それほど時間はかかりません。勿論個人差はあるでしょうが、一度やっていることでもあります。
2015-08-22 21:04:50 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
1年分あたり、長くとも一ヶ月程度もあれば十分でしょう。判っているところは確認するだけで良いので、短時間ですみます。一ヶ月はベタっとやり直しする場合を想定しています。実際には、1年分あたり数日~数時間程度で済むのではないかとかんがえられます。
2015-08-22 21:06:42 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
ただし、それぞれの学年相応の「国語力」は必要です。中学校履修範囲については、明治図書の「整理と対策」という教材が非常に優秀で良かったのですが、現在一般書店での入手ができません。復習目的の方は、過年度版をオークションなどで探すと良いでしょう。(現役生は学校で購入できます。)
2015-08-22 21:07:28 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
教科書ガイドはかなり詳細な解説が書かれており内容的には申し分ないのですが、如何せんかなり高価です。(しかも学年あたり1教科1冊です。)「チャート式」かそれに類する「単元のまとめつき」参考書は良いでしょう。演習も必要ではありますが、それは理解できた後で考えましょう。
2015-08-22 21:11:39それより、教科書に掲載されている問題を全部解いてしまうほうが重要です。
 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
話を戻しましょう。「解説を読んでもわからない」原因の2つ目です。それは「ある程度のボリュームがある文章を読み進めるうちに、増え続ける情報を処理しきれずパニックを起こしている」ことです。両方の要因が同時に関わってくると悲惨です。人間の脳は、そこまで優秀ではありません。
2015-08-22 21:12:04 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
普段取り扱っていない多くの事柄や関係を随時把握するのはとても難しいのです。そこで、文章を読み進めながら(問題を解くために必要な)情報をピックアップし、関係をメモします。図を描いても良いでしょう。こうして書き出すことによって、頭の中も整理できます。
2015-08-22 21:12:51 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
一見して明らかに、どう解き進めれば良いかがわかるような問題であればいきなり式を立て始めることもあります。しかし、問題を読みながら情報の整理するケースは少なくありません。ここで重要な作業があります。それが「問題の分解」です。
2015-08-22 21:13:12 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
全体を俯瞰しても解き方がわからないなら、わかるところまで分解すれば良いのです。典型的なのは「三平方の定理」を学んだ直後に提示される「直方体の対角線の長さを求める問題」です。「三平方の定理」は、直角三角形に適用される、辺の長さの関係を示す定理です。
2015-08-22 21:16:16 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
図を見てください。直方体の中で線分EGに補助線を書き足すことによって、三平方の定理を二回使う問題に分解できます。この補助線も「どこに引けば良いかわからない」という質問が多く寄せられます。ここで重要なのが、これまでの蓄積です。 pic.twitter.com/ctUwNs7DFJ
2015-08-22 21:17:33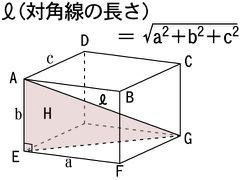 拡大
拡大
 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
直面している(解かなくてはならない)問題を自分が知っている(解ける)問題に近づけていくのです。ということは、図形の基本的な性質をひと通り把握しておかないと、目的地がわかりません。中学校で、例えば図形なら三平方の定理、メラネウスの定理、トレミーの定理、中点連結の定理、接弦定理など。
2015-08-22 21:18:32 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
この辺りの基本定理と各図形の基本的な性質が「目的地」となるでしょう。定理が頭に入っていないと、こればっかりはどうしようもありません。また、定理の証明も教科書には記載されていますが、この証明の手順は、図形の問題を解く手順としての手がかりにもなるのです。
2015-08-22 21:20:06 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
次。質問の時に良く「いまいちピンときません」と言われます。「これ、進研ゼミでやったところだ!」などという展開を期待しているのでしょうか。全く同じ形式の問題(しかも解き方を完全に覚えている)でもない限り、そうは問屋が下るしません。問題を見ただけで「わかりません」など論外です。
2015-08-22 21:21:00 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
ここで「考えろ」と言われるわけですが、この「考えろ」には多くの手順や操作が含まれています。これについては後で解説します。例えば前述の「問題の分解」も「考えろ」に含まれる操作です。数学で問われるのは単なる記憶力ではありません。「二次方程式の解の公式を書け」なんて問題は出ません。
2015-08-22 21:22:40 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
数学の試験で求められるのは次の技能であることをしっかり認識しましょう。 まず「問題を分析・分解する」力、そして「知っている中から適切な解法を選び」、その問題分析の結果を「知っている解法が使える形に近づけ」、「解法を適用して処理し、解を得る」ことです。
2015-08-22 21:23:42 美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
美星まどい/bp@THEXDER勝手に移植の人
@beautyplanets
これが「考えて答えを出す」という言葉の意味です。「教科書が優れている」と繰り返し述べているのはまさにこの点で、例題のマネをすれば問題が解けるようになっています。これが「知っている解法が使える形に近づける」訓練になるのです。以上を念頭において学習すると成果を上げやすいと考えます。
2015-08-22 21:24:08