-
 groebner_basis
groebner_basis
- 9451
- 37
- 2
- 0
 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題①】 今日は、「ディクソンの補題」という、グレブナー基底の存在性を証明するのに、 重要な補題を証明するぶなっ! 今回、知っているといい知識は、 イデアルbit.ly/1GOnfjP ぶなよっ!
2015-10-21 20:12:31 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題②】 では、主張の前に用語を定義するぶな! 【定義:単項式イデアル】 多項式の集合 I が単項式のみにより生成されているイデアルのとき、 Iを単項式イデアルとよぶ。 つまり、ある単項式だけの集合Aがあって、 I=<A> である。
2015-10-21 20:15:59 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題③】 例えば、K[x,y]において、I=<x*y, y, x^2*y^3> は単項式イデアルになっているぶな!なぜなら、x*y,y,x^2*y^3はすべて単項式ぶな! 一方、J=<x+y>は、x+yは項が2つあり、単項式ではないので、単項式イデアルではないぶな!
2015-10-21 20:20:19 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題④】 では、ディクソンの補題ぶな! 「ディクソンの補題」 I=<A>を単項式イデアルとする。 このとき、Aから有限個の単項式f_1,…,f_sを選ぶことで、I=<f_1,…,f_s>とできる。特に、Iは有限生成である。
2015-10-21 20:24:01 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑤】 この補題の意味を説明するぶな! イデアルとは、f,g in Iと多項式hに対し、 ・f+g in I ・h*f in I を満たす集合だったぶな。 つまり、一般にイデアルは無限個の元を持っていて、 有限個の基底を持つとは分からないぶな!
2015-10-21 20:27:51 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑥】 ディクソンの補題は、Iが単項式イデアルなら、 有限個の基底を取ることができるということを主張しているぶな! では、補題を証明していくぶな! 【証明】 簡単のため、K[x,y]の場合で証明するぶな。 また、I=<A>を単項式イデアルとするぶな。
2015-10-21 20:31:04 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑦】 図のようにK[x,y]の中で、単項式イデアルをイメージするぶな。 証明の方針としては、まずK[x]にイデアルを射影した(つぶした) イデアルを考えて、その生成元とyの情報を使って、イデアルをスライスするぶな。 pic.twitter.com/usNPcByUA6
2015-10-21 20:34:03 拡大
拡大
 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソン⑧】 〔Step 1.イデアルをつぶす〕 k[x]のイデアルJを J=<x^a | あるbがあって、x^a*y^b in I> と定めるぶな! つまり、K[x,y]のイデアルIの元のうち xだけの成分をとったものぶなっ! pic.twitter.com/A9vspRHPym
2015-10-21 20:41:29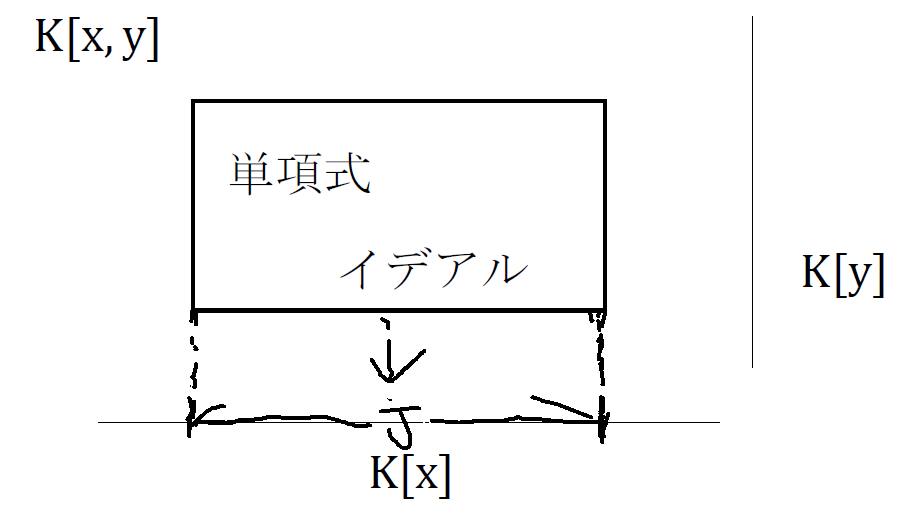 拡大
拡大
 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソン⑨】 ここで、実はJはたった一つの元から生成されるぶな。 その生成元としては、Jの中で、(0以外の)最も次数が小さいもの f をとるぶな! すると、Jの任意の元gに対し、gをfで割って、 g=h*f + r となった時、r はfより次数が小さいぶな!
2015-10-21 20:45:53 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソン⑩】 すると、f の次数の最小性から、r=0となるぶな。 よって、g=h*f となり、J=<f>が言えたぶなっ! ここで、Jは単項式イデアルなので、f=x^aとするぶな。
2015-10-21 20:50:30 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑪】 〔Step 2: yの情報を得る〕 ここで、Jの定義から、あるbがあって、x^a*y^b in I になるぶな。0≦i≦b なる各iに対し、 K[x]の単項式イデアルJ_iを J_i = <x^c | x^c*y^i in I> と定義するぶな!
2015-10-21 20:55:38 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑫】 つまり、J_iとは、Iの中で、y^i の成分を持つものをx方向につぶしたものに なっているぶな!Jと同じように、J_iもある単項式x^{a_i}があって、 J_i=<x^{a_i}>となるぶなっ! pic.twitter.com/bXdCxx0tr2
2015-10-21 21:01:53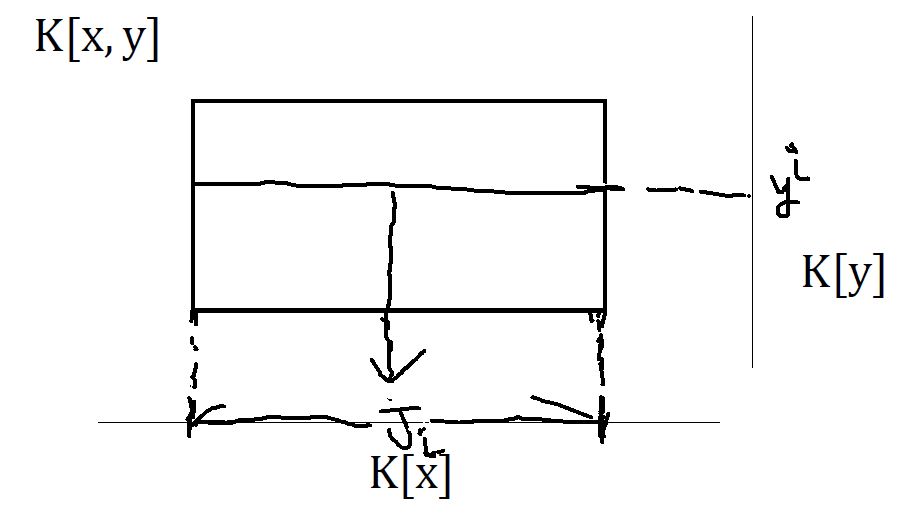 拡大
拡大
 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑬】 ここで、J_iの定義から、x^{a_i}*y^i in I になっているぶな。 (ちなみに、I にy^iなる成分がないとき、J_iは{0}とするぶな。) これで、Iの基底を作る準備は整ったぶなっ!
2015-10-21 21:05:58 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソン⑭】 〔Step3:基底を作る〕 x^{a_1}*y, x^{a_2}*y^2, … x^{a_{b-1}}*y^{b-1}, x^a*y^b はIの基底になっていることを示すぶな! これはイデアルをスライスしてるぶな pic.twitter.com/dcSmyH1ylG
2015-10-21 21:17:58 拡大
拡大
 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑮】 x^c*y^p をIの元とするぶな。 この元は、上のリストの中のどれかで、割り切れることを示すぶな。 p≧b のとき、x^c in J から、x^cはx^aで割り切れるぶな。 y^pはy^bで割り切れるので、x^c*y^pはx^a*y^bで割り切れるぶな。
2015-10-21 21:23:35 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソン⑯】 p<bのとき、x^c in J_p ぶなから、x^cはx^{a_p}で割り切れるぶな。 よって、x^c*y^pはx^{a_p}*y^pで割り切れるぶな。 したがって、Iの任意の元は、上のリストで割り切れることが分かり、I=<上のリスト>で、Iは有限生成ぶなっ!
2015-10-21 21:28:24 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
【ディクソンの補題⑰】 上のリストの元は、I=<A>の元ぶなから、上のリストをAの元で置き換えてもいいぶな。(例えば、x^a*y^bがAの元f_1で割り切れたら、x^a*y^bをf_1で置き換えてよいぶな。) よって、これでディクソンの補題が証明できたぶな!!
2015-10-21 21:39:58 グレブナー基底大好きbot
@groebner_basis
グレブナー基底大好きbot
@groebner_basis
今日の参考文献も、グレブナ基底と代数多様体入門ぶなッよ!togetter.com/li/877168
2015-10-21 21:43:27