「かけ算の順序」なんてもう古い⁈ 今や時代は「足し算の順序」‼︎
-
 kuri_kurita
kuri_kurita
- 577367
- 2898
- 685
- 5295
 日本農園
@nihonnouen
日本農園
@nihonnouen
これがかの有名な足し算や掛け算の順番が逆でバツになるってやつか…。最初9+5って書いてたら「あとから9台来たんだから5+9じゃないとダメ」と言われてバツにされたらしい。どうにも納得いかんがここで反抗しても仕方ない pic.twitter.com/XYuMhGxxAC
2015-11-17 21:06:15 拡大
拡大
 日本農園
@nihonnouen
日本農園
@nihonnouen
先生は先生でこう教えろという決まりがあるんだろうからな。たとえ先生自身が納得してなくても指導要領には逆らえないだろうから先生に文句言っても板挟みで気の毒なだけだ
2015-11-17 21:07:39 積分定数
@sekibunnteisuu
積分定数
@sekibunnteisuu
@nihonnouen #掛算 指導要領に「掛け算や足し算の順序をちゃんと指導するように」と書いてあるわけではありません。かといって、教師が個人的にやっているわけでもなくて、算数教育界の権威とされる人たちがおかしな教え方を推奨しています。
2015-11-17 21:38:39 積分定数
@sekibunnteisuu
積分定数
@sekibunnteisuu
@04uran92 黒木玄さんの連ツイのつづきをみれば種明かしがされます。 算数教育では 男子4人、女子3人、みんなで何人? 4人いるところに3人やってきた。何人になった? この2つを、「異なる足し算の場面」として、前者を「合併」、後者を「増加」として区別します。
2015-11-06 17:02:59 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#掛算 #足算 子どもが4人いるところにあらたに子どもが3人やって来た。銀林浩氏曰く「意味の上からは確かに 4+3≠3+4 であって厳密には交換法則は成立しない。この両辺の《値》が等しくなるのは、ただの結果にすぎない。」これもすごすぎ。 pic.twitter.com/QEHTOIGm
2012-11-09 10:23:40 拡大
拡大
 積分定数
@sekibunnteisuu
積分定数
@sekibunnteisuu
@genkuroki @temmusu_n #掛算 足し算の順序に拘る教科書 日本文教出版「しょうがくさんすう 1ねん」 pic.twitter.com/1mSkC0397X
2015-05-06 22:52:18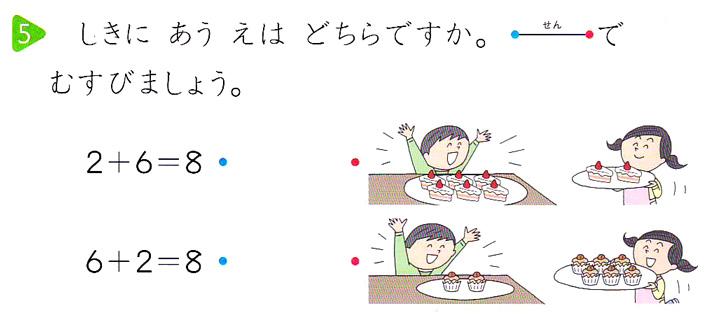 拡大
拡大
(注:↑ この問題は 2015年版の教科書にはないとのことです。末尾に追記あり)
 天むす名古屋 Temmus 𓃠
@temmusu_n
天むす名古屋 Temmus 𓃠
@temmusu_n
#掛算 足算の順序を区別する教科書が2011年度から使われています。日本文教出版37頁にケーキが2個あるところに6個運ばれてくる図と数字を逆にした図に対応する足算の式を求める問題があります。指導書によるとそれぞれ別の式が正解です。詳しくはbit.ly/VlAuDy。
2013-01-02 21:35:50↓ 下記のリンク、アクセスしやすいようにまとめ公開後に追加しました。 4社分の2011年版教師用指導書に、算数教育専門家の標準的な方針が表れていることがわかります。
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@genkuroki #掛算 証拠物件その2。ある小1の教科書より。足し算も順序が逆なら誤り。男子と女子の視点を入れ替えるという発想にも欠けている。色々な意味でダメ過ぎる。掛算順序強制は問題全体の氷山の一角にすぎない。 pic.twitter.com/0buTDDnGkP
2015-04-10 12:29:41 拡大
拡大
 k u r i t a 🐈⬛ 🐈 𓃭 𓃠
@kuri_kurita
k u r i t a 🐈⬛ 🐈 𓃭 𓃠
@kuri_kurita
『子どもが5人います。そこに3人きました。子どもは( )8人になりました。 この文章の( )に当てはまる言葉を書くのですが娘は(あわせて)と書いてバツをもらってきました。 正解は(ぜんぶで)なのだそうです。』 detail.chiebukuro.yahoo.co.jp/qa/question_de…
2015-11-18 07:28:17 林 衛
@SciCom_hayashi
林 衛
@SciCom_hayashi
@Rsider @genkuroki 研究室卒業生が小学1年算数指導で苦労したのは,「あわせていくつ」「ふえるといくつ」を区別する文章題をつくらせる研究授業。どちらも同じ足し算だとふつうに理解できるのに,わざわざちがうものだと強いてしまうので子どもたち大混乱。無理に教えるのが無理
2012-01-13 17:36:25 林 衛
@SciCom_hayashi
林 衛
@SciCom_hayashi
@darkboysandmen shinko-keirin.co.jp/sansu/WebHelp/… のことですか。これも足し算の「あわせていくつ」「ふえるといくつ」同様,無理に区別するからかえってわからなくなるような。そのために掛け算に順番?@Amy_mishima @Rsider @genkuroki
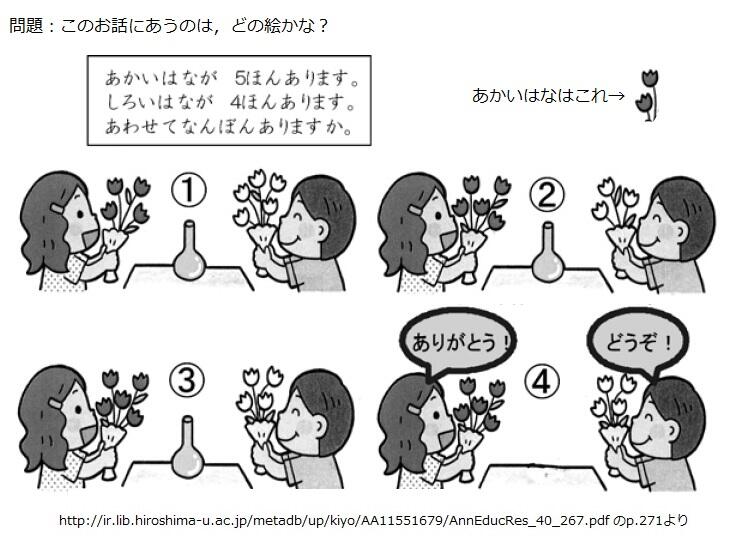
2012-01-14 01:49:03ではここで問題です。
下の画像は「お話にあう」絵を選ぶという小学一年生の算数の問題で、答えは③なのだそうです。
では、なぜ④ではいけないのか、その理由を考えてみてください。
ちなみに、「創造性を育む」のが目的の授業だそうです。
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#掛算 件の論文の結論より【本授業では、創造性を育むために、二つの「種蒔き」をしている。一つは「増加」の絵で、もう一つは「被加数と加数の関係」である。一つ目の「増加」については、子どもの発言をもとに、矢印でたすことの向きを示した。】w pic.twitter.com/GIgANG6uRK
2014-06-04 17:08:01 拡大
拡大
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#掛算 一つ前のツイートの画像を見て嗤ってしまった人は多いと思う。しかし先生Tによる「矢印」と同趣旨の図が算数の検定教科書にも載っていることを知れば嗤うだけではすまないことを納得するのではないか?(嗤うこと自体は普通だと思う。) pic.twitter.com/K2HonAvScX
2014-06-04 17:11:27 拡大
拡大
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#掛算 続き。東京都教職員研修センター平成17年度報告集 kyoiku-kensyu.metro.tokyo.jp/09seika/report… より pic.twitter.com/xfwajDloy0 。 掛算の順序強制問題は「算数の教え方を指南する立場の人たちがトンデモ化している」という大きな問題の氷山の一角。
2014-06-04 17:19:37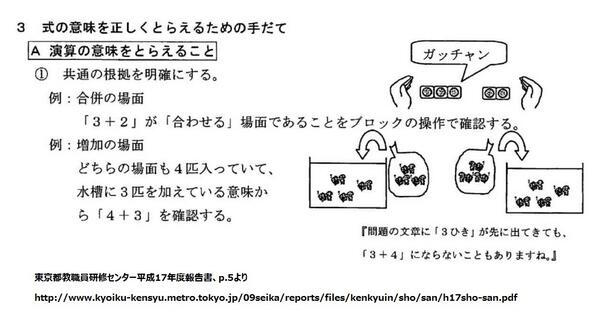 拡大
拡大
 鰹節猫吉
@sunchanuiguru
鰹節猫吉
@sunchanuiguru
#掛算 鹿児島大学附属小学校の算数授業研究→ edu.pref.kagoshima.jp/curriculum/sid… ガッチャンコと合体するたし算と、ピューっときて合体するたし算は違うから区別しないといけない。(泣泣泣……) pic.twitter.com/JwbBSGNbZ3
2014-07-15 00:27:46 拡大
拡大
 k u r i t a 🐈⬛ 🐈 𓃭 𓃠
@kuri_kurita
k u r i t a 🐈⬛ 🐈 𓃭 𓃠
@kuri_kurita
バカじゃないの、この算数のセンセ。→『合併の場面をより意識させるために、後から入れた金魚はいじめられやすいという金魚の性格を話し、同時に水槽に移す方がよいことに気付かせる』 twitter.com/sunchanuiguru/… 「算数の“たしざん”」の授業だぜ!
2014-07-15 00:34:29