-
- いいね！132
Σ(ﾟДﾟ)
「数列」の単元に、忽然と姿を現す ∑ という記号。
初めに出てきたとき、「うわぁ、なんじゃこりゃ」と思う人が多いのではないでしょうか? (実は私もその一人)
でも、意味が分かれば、「なるほどなあ」と納得できると思います。
このまとめが皆さんの理解への助けになればなあと思います。
∑の記号の意味
き@はみ禁
@TomoK0827
【∑の記号①】例えば、数列{a(n)}を、a(n)=3n-2で定めます。この時、初項から第n項までの和S(n)は、 S(n)=(3*1-2)+(3*2-2)+(3*3-2)+…+(3*n-2) と書けますね。 pic.twitter.com/eB8XG9Z57J
2015-12-10 23:19:22
拡大
き@はみ禁
@TomoK0827
【∑の記号②】でも①の式は少し長いし、何度も書いていると疲れます。そこで、このような＋の記号を繰り返す記法の代わりに、簡単にひとまとめに書ける∑の記号が導入されたのです。
2015-12-10 23:31:17長い記法をずっと使うと疲れるため、短く書き表すために、∑という記号を用いるんですね。
では、∑を使うと、この長い和の式をどう書き表せるというのでしょうか...
き@はみ禁
@TomoK0827
【∑の記号③】数列{a(n)}において、a(1)+a(2)+…+a(n)のことを下の図のように書き表します。(tweet上では∑[k=1→n](a(k))と書きます) ∑の下のk=1でkの値を1から1ずつ、上の値nまでずらします。 pic.twitter.com/yNQsVE2zWc
2015-12-11 00:01:48
拡大
∑の下に「k=1」と宣言すると、
- 「∑の右側の式のうちで、kがあれば、そいつが変わっていくときの和をとりますよ」
- 「そしてその変えるkの最初の値は1で、1個ずつ変わっていきますよ」
ということを表します。
そして、∑の上の数、ここでは「n」で、
- 「変える文字(ここではk)の値をnまで変えますよ」
ということを宣言します。
き@はみ禁
@TomoK0827
【∑の記号③補足】∑の下にある「最初の値」は1であることが多いですが、0からだったり、2からだったり、はたまたn+1からだったりします。 画像の緑の「かえるもじ」はkでなくてもよいですが、「最初の値」や「最後の値」に文字が出てくるときは、それらを避けて別の文字にしておきましょう。
2015-12-11 00:18:39もちろん、∑の上に書く「最後の値」も、下に書いてある「最初の値」より大きければ何でも構いません。
き@はみ禁
@TomoK0827
【∑の記号④】先ほど、①で出てきた数列a(n)=3n-2について、その初項から第n項までの和のことをシグマを用いて表すと、次のようになります。 pic.twitter.com/owmWtRsf1e
2015-12-11 00:13:34
拡大
∑の記法の練習
き@はみ禁
@TomoK0827
【∑の記号⑤】∑の記号で書かれた和を、＋を用いたものに書き換えたり、その逆をしたりといった練習をしておきましょう。 例えば、次の∑で書かれた和を、＋を繰り返した書き方に直してみましょう。(1)はそのあと、実際に和を求めてください。 pic.twitter.com/qhoOMfVO8t
2015-12-11 00:33:51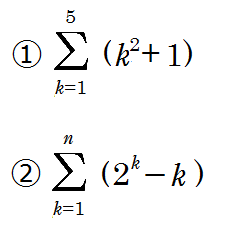
拡大
き@はみ禁
@TomoK0827
【∑の記号⑤補足】「かえるもじ」がkで、∑の右にある式にkが複数ある場合は、すべてのkを一斉に「最初」から「最後」まで動かします。 ちなみに後で出てくるのですが、∑の右の式に「かえるもじ」以外のものがあった場合は、そいつはいじってはいけません!
2015-12-11 00:37:22
き@はみ禁
@TomoK0827
【∑の記号⑤解答】①下にk=1とあり、上に5があるので、kを1から1個ずつ、5まで動かしながら足します。すなわち、kを1，2，3，4，5にした時の式の値をすべて足しますから、画像のようになります。これを計算すると60になります。 pic.twitter.com/XnKCBvnh6h
2015-12-11 22:51:35
拡大
き@はみ禁
@TomoK0827
【∑の記号⑤解答】②下にk=1とあり、上にnがあるので、kを1から1個ずつ、nまで動かしながら足します。すなわち、kを1，2，3，…, nにした時の式の値をすべて足しますから、画像のようになります。 pic.twitter.com/SETyYYJdd9
2015-12-11 22:52:50
拡大
さて、ここまで来ると、まあなんとなく∑の記号の意味するところは分かってきたと思います。(「全然わからん」という人はここからは立ち入り禁止!)
でも、∑の式が書けても、∑の計算ができないと、この記号を使った意味がないように感じると思います。
ここからは、∑を使ってある程度の和を求めることを目標とします。
∑の線型性と和の公式
注) ここでは定理や公式、およびそれを用いた計算例や練習問題を提示するにとどまり、証明に関してはお手元の教科書・参考書を見るか、ググってください。
き@はみ禁
@TomoK0827
【∑の記号⑥】ここからの主な内容は、∑を具体的に計算することです。∑の計算ができると、あとでいろいろなことができるようになります。 ∑はたし算引き算で分解でき、定数倍を∑の外に出せます。それが「∑の線型性」というものです。 pic.twitter.com/REPkhA5qx2
2015-12-11 23:23:07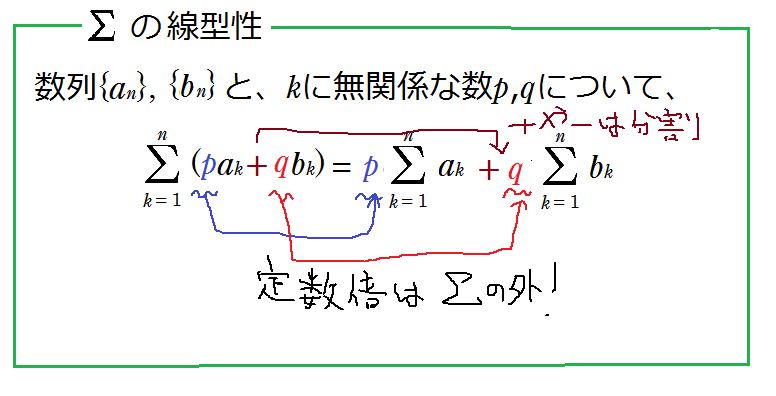
拡大
き@はみ禁
@TomoK0827
【∑の記号⑥補足】⑥画像に「kに無関係な数p,q」とあります。∑の下にk=1とあるので、「かえるもじ」はk。すると、p,qがkを使ったものだと、p,qがkの値によって変わってきてしまうので、うまく∑の外には出せなくなります。だから、このp,qはkと無関係である必要があります。
2015-12-11 23:27:25「線型性」というなんか難しい言葉が出てきましたが、簡単に言うと、何かものを表す記号fが、
- たし算によって分解できる すなわち f(x+y)=f(x)+f(y)
- 定数倍はfの外に出せる すなわち xに無関係な定数kに対し、 f(kx)=kf(x)
の2つを満たすことです。微分記号・積分記号などがこんな性質を持っていましたね。そしてこれら2つはまとめて、
- xとyに無関係な定数p,qに対し、f(px+qy)=pf(x)+qf(y)
と書けます。ここでp=1, q=-1とすれば、fは引き算でも分解できることもわかります。
最低限覚えるべき(使えるべき)公式
き@はみ禁
@TomoK0827
【∑の公式⑦】さて、大事な暗記公式4つ! 定数と、k,k^2,k^3の和の公式です。(証明はここではしませんが、教科書などには載っているかと思います。) pic.twitter.com/mEbeGotJFr
2015-12-11 23:35:56
拡大