-
- いいね！0
Καῖνος
@derived_kai
Lemniscate の 3 等分方程式の Galois 群を計算しようとしたけど、高次過ぎて Sage のアルゴリズムでは無理なので Magma を使えと言われたけど Magma 持ってないです (^^)
2013-01-30 10:06:00
@yokoemon2112
@_Cargese すみません、計算機でごまかしました（笑） Magma, Asir, Sage, Maple の4実装で全て同じ群構造が出た（し、少なくとも2つは違うアルゴリズムを使っている）ので、信頼していいかと思います。
2013-01-30 15:26:36
Καῖνος
@derived_kai
位数から間違えてた、16 という事は Galois Closure の計算で確定していたのに… √-1 の作用があると思って C_{4} 含むと思ったけど、√-1 は根の置換は引き起こすけど体の同型からは誘導されないものだった…
2013-01-30 15:26:40
Καῖνος
@derived_kai
@yokoemon2112 ありがとうございます．ぼくも計算機でやってみたところ C_2 の 4 つの直積と返ってきました（Transitive group number 12 of degree 16）．ちなみに Lemniscate の 3 等分方程式として表れる方程式です．
2013-01-30 15:59:59
Καῖνος
@derived_kai
G = L.galois_group(type='pari') などで計算してくれました．http://t.co/loq4GcA7
2013-01-30 16:01:16
Καῖνος
@derived_kai
ちなみに根は楕円関数を用いて計算できて、次の様に．位数さえ分かれば，ここから具体的に作用を求めることができるかもしれない． http://t.co/CrcKrlrY
2013-01-30 16:07:57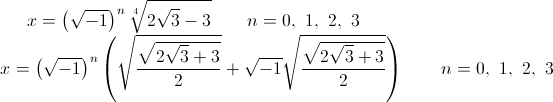
拡大
Καῖνος
@derived_kai
根の複素平面上の配置は次のよう．-1 倍と複素共役と，あと二つ二次巡回群の作用があるはずだけど． http://t.co/SwADnfHb
2013-01-30 16:22:01
拡大
kyo@math
@kyon_math
@_Cargese (-1)倍はガロア群の作用じゃないですね．a+b√2 → a-√2 みたいなのはガロア群の作用．＃(-1)倍すると単位元がとんでもないことに
2013-01-30 16:39:30
Καῖνος
@derived_kai
根は楕円 Lemniscate 関数を用いて（0 を含む）次のように書けていて，そこから分からないかと思ったけどよく分からないなあ．基本周期を使って書いた方がいいかなあ．むう． http://t.co/aijvqGzb
2013-01-30 17:35:30
拡大
Καῖνος
@derived_kai
@yokoemon2112 なので Abel 群であることは分かっていたのです :) （横山さんが教えてくれると期待してツイートしてました（笑）ありがとうございます。）
2013-01-30 17:38:16
Καῖνος
@derived_kai
なんか見つかりました．．．'The Galois theory of the lemniscate' http://t.co/s1oqE06C Cox の 'Galois Theory' は Galois 理論の本では珍しく Lemniscate を扱っていました．
2013-01-30 17:39:54
@yokoemon2112
@_Cargese いやはや、お恥ずかしい（笑）でも8次のわりと単純な Galois 群とはいえ1秒くらいで計算が終わったことに驚きましたｗ また面白い問題が見つかったら教えてください＾＾
2013-01-30 17:41:17
Καῖνος
@derived_kai
さっきの方程式の正の実根を ω として，Q(√-1)(ω)/Q(√-1) の Galois 群を計算しているようだ．結果はより一般に奇数 n に対する n 等分方程式について，G=（Z[√-1]/nZ[√-1] の単数群）．類体論と虚数乗法がどうたらと書いてある．
2013-01-30 17:55:01
Iwao KIMURA
@iwaokimura
y^2=4x^3-(1/4)xの3等分点をQに添加して得られる体のQ上のGalois群は，3等分点の加群(Z/3Z)^2の自己同型群の部分群になるので，Galois群の位数は48を割るはずですね． @_Cargese @yokoemon2112
2013-01-30 18:11:13
Iwao KIMURA
@iwaokimura
後は，虚数乗法があることから，3等分点の加群をZ[i]加群とみると，Z[i]加群としての自己同型群は (Z[i]/3 Z[i])^* になるはずなので，Galois群の位数は8で割れるはず．…位数は決められないのかな．Rosenの http://t.co/mPtZrHYw も．
2013-01-30 18:13:56
Καῖνος
@derived_kai
@cocoatomo はじめまして．今お気に入りにして頂いた発言は間違いだったのでお気を付け下さい．．．二次の巡回群の四乗が正解です (C_2)^4．
2013-01-30 18:19:51
Καῖνος
@derived_kai
iwaokimura さんが教えてくれたものは Shilverman，Tate 'Rational Points on...' に ’Galois Representation Theorem’ として載っていました．
2013-01-30 20:10:38
Καῖνος
@derived_kai
@iwaokimura @yokoemon2112 むむぅ... y^2=4x^3-(1/4)x はどこから導いたのでしょうか．Galois 群は Abel 群なので，SL(2,F_3) の部分群と言えそうな気がしているのですが，すると位数が 16 に反するような気がしています．
2013-01-30 20:42:02
Καῖνος
@derived_kai
ω=sln(4K/3) とすると，Q(ω)/Q は ω の Q 上の最小多項式が x^8+6x^4-3 なので拡大次数 8．この多項式の分解体は Q(ω)(√-1)/Q なので，Galois 群の位数は 16．
2013-01-30 20:46:50
Iwao KIMURA
@iwaokimura
@_cargese あ，私は件の楕円曲線の3等分点を付加した体の事を考えていました．問題なのは，レムニスケートの等分点を付加した体なんですね．その違いを議論しているのが，確かに 1208.2653v2 ですね．
2013-01-30 23:01:19