-
 Polyhedrondiary
Polyhedrondiary
- 4894
- 0
- 0
- 0
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
【本棚登録】『ミッション解析と軌道設計の基礎』半揚 稔雄 booklog.jp/item/1/4768704… #booklog
2018-01-31 06:50:03『惑星探査機の軌道計算入門』がきっかけ
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
半揚先生の入門書の次はこっち読んでる。 本格的な軌道の教科書って感じ twitter.com/Polyhedrondiar…
2018-01-31 08:02:54ホーマン遷移と双楕円遷移
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
遷移する前後の軌道半径の比が11.94より小さい場合は,いつでもホーマン遷移(P,Qの2点でエンジン吹かす)がΔVの総和を最小にするが,半径比がさらに大きくなると,もっとエネルギーを節約できる遷移軌道が存在する。 丁寧な解説と計算でようやく理解した。 pic.twitter.com/ZUG6wJRHO4
2018-01-31 08:07:00 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
投入する円軌道よりも遠くに飛ばして,その遠心点でΔVを加える3インパルスマヌーバがそれで,双楕円遷移軌道と呼ばれている。 PからIまでと,IからQまでの双子の楕円を使う pic.twitter.com/WHo9nRps3W
2018-01-31 08:13:58 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
Iをどこにするかには自由度があるけど,遠くに飛ばすほど節約になって,無限遠でΔVを入れる「双放物線遷移軌道」が一番エネルギー的にお得。 でも,その軌道遷移にはもちろん無限大の時間がかかるので,実用性は皆無である。
2018-01-31 08:17:13軌道面変更でも同様の議論が
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
軌道面変更についても同様に,一旦遠くに行って戻る方が効率が良い場合がある。 遷移前後の円軌道が同一半径のとき,軌道交点における1インパルスで軌道面変更は可能(上図)だが,軌道面変更角が大きい場合は3インパルス遷移(下図)の方が有利になる。p.113 pic.twitter.com/vNsMqCpwWW
2018-01-31 08:20:31 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
今まさに皆既月蝕だけど,タイムリーにも軌道計算の本を読んでる twitter.com/Polyhedrondiar…
2018-01-31 22:03:14双放物線遷移(←長半径無限大の双楕円遷移)
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
この双放物線遷移軌道だけど,無限遠で加えるΔVの大きさは無限小であるというのが最大の萌えポイント。 twitter.com/Polyhedrondiar…
2018-01-31 22:05:34 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
無限の彼方で無限に小さい噴射をして,無限大の時間をかけて軌道を移るのが最も効率的だとか言うんだから,ロマンを感じざるを得ない。p.110 pic.twitter.com/2hHwwnpM2w
2018-01-31 22:08:27 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
ただしさっきの図くらい軌道半径の比が小さいときはホーマン遷移軌道が最も効率的なことに注意。 双放物線遷移軌道が有利になるのは半径比ρが11.9387654…以上のとき(数値は三次方程式の解)p.111 pic.twitter.com/o8mjuZ6Vvf
2018-01-31 23:32:23 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
ホーマン遷移軌道と双放物線遷移軌道でΔVの総和が等しいと置いたときの半径比が満たす三次方程式がこれ。 3つの実解のうち小さい2つは1以下なので不適というわけ。 pic.twitter.com/pxir3Vm59J
2018-02-01 08:18:49 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
軌道遷移,インターセプト,ランデブーと難易度が上がっていくことなど,なるほど納得。 弾道ミサイル迎撃はまさにインターセプトの一例で,同じ時刻に位置ベクトルを合わせる軌道制御が課題となっている。 これがランデブーだとさらに速度ベクトルも合わせないといけない。
2018-02-01 08:32:01 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
古典的なニュートン力学,しかも摩擦とか考えないし質点近似でシンプルな前提のはずなのに,軌道力学めっちゃ内容に富んでいて面白い…! twitter.com/Polyhedrondiar…
2018-02-01 08:26:28人工衛星は球対称でない地球重力ポテンシャルを活用してた
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
人工衛星の軌道についても詳しい。 よく使われる太陽同期軌道や地表回帰軌道は,地球が球でないことによる摂動(永年摂動)を巧みに利用してるっていうのは目から鱗だったし激しく納得。 ↓軌道面と太陽がなす角を一定に保つ太陽同期軌道。p.340 pic.twitter.com/toSOZc1zQn
2018-02-07 08:13:08 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
地球は極方向に潰れた回転楕円体なので,軌道面を赤道面に引き寄せるような力が働いて,それによる歳差運動で軌道面が回転する。 人工衛星が地球の自転と同じ方向(西から東)に飛ぶ場合,軌道面は反対回りにズレていくp.304 pic.twitter.com/jx432ld6wF
2018-02-07 08:19:15 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
太陽同期軌道と地表回帰軌道の双方の条件を満たす太陽同期回帰軌道。 軌道の長半径,傾斜角,離心率を適切に選ぶことでこのような軌道設計が可能となる。人間って賢いなあ。p.344 pic.twitter.com/OnJVChTSi9
2018-02-07 08:25:37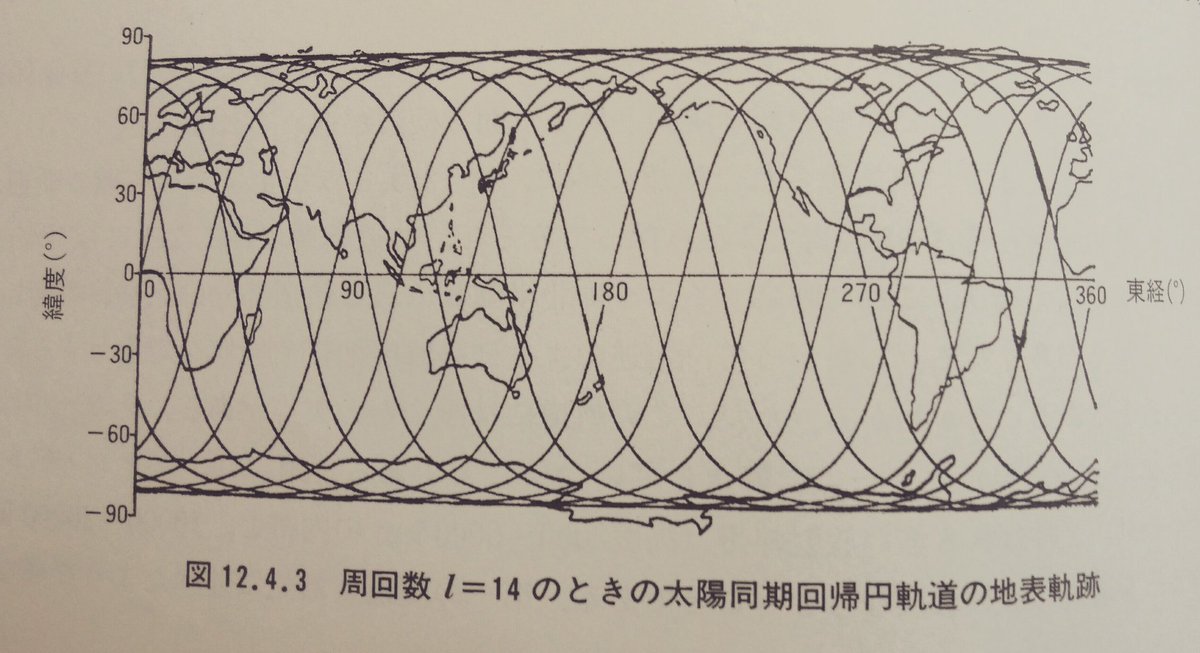 拡大
拡大
 {3,5/2} 大二十面体
@Polyhedrondiary
{3,5/2} 大二十面体
@Polyhedrondiary
西側から東側に飛ぶ人工衛星の軌道面は逆行してしまうので,この動きを順行する地表や太陽方向に合わせるには,反対回りに飛ばさないといけない。 つまり,軌道傾斜角は90°を超える必要があり,打上時の地球の自転効果の意味は薄い。(そうだったのか!)p.342 pic.twitter.com/JpSPyVCG53
2018-02-07 08:32:49 拡大
拡大