-
 nakaZAWAHIDEKI
nakaZAWAHIDEKI
- 4695
- 0
- 0
- 22
 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキ - 色彩魔方陣 aloalo.co.jp/nakazawa/2014/… #色彩魔方陣 Hideki Nakazawa - Colored Magic Square aloalo.co.jp/nakazawa/2014/… #Colored_Magic_Square
2014-12-04 05:54:34 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣 pic.twitter.com/M9KjYtP0mH
2014-12-04 05:57:26 拡大
拡大
 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
魔方陣とは? What Is Magic Square? 4|9|2 3|5|7 8|1|6 各列の和=15 各行の和=15 魔方陣 - Wikipedia ja.wikipedia.org/wiki/%E9%AD%94… #魔方陣は魔法陣ではにゃい #色彩魔方陣
2014-12-04 06:01:00 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
3次方陣 3x3 Magic Square aloalo.co.jp/nakazawa/2014/… #色彩魔方陣 pic.twitter.com/fK0noKHwSR
2014-12-04 06:04:33 拡大
拡大
 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣第一番 Colored Magic Square No. 1 2014 油彩、キャンバス 540x540 備考1:3次方陣 備考2:C基本形+M左右対称+Y天地対称 aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣
2014-12-04 06:09:11 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣第二番 Colored Magic Square No. 2 2014 油彩、キャンバス 681x681 備考1:3次方陣 備考2:C天地対称+M基本形+Y左右対称 aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣
2014-12-04 06:10:12 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣第三番 Colored Magic Square No. 3 2014 油彩、キャンバス 720x720 備考1:3次方陣 備考2:C左右対称+M天地対称+Y基本形 aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣
2014-12-04 06:11:06 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
4次方陣 4x4 Magic Square aloalo.co.jp/nakazawa/2014/… #色彩魔方陣 pic.twitter.com/X11MHu6ts4
2014-12-04 06:12:25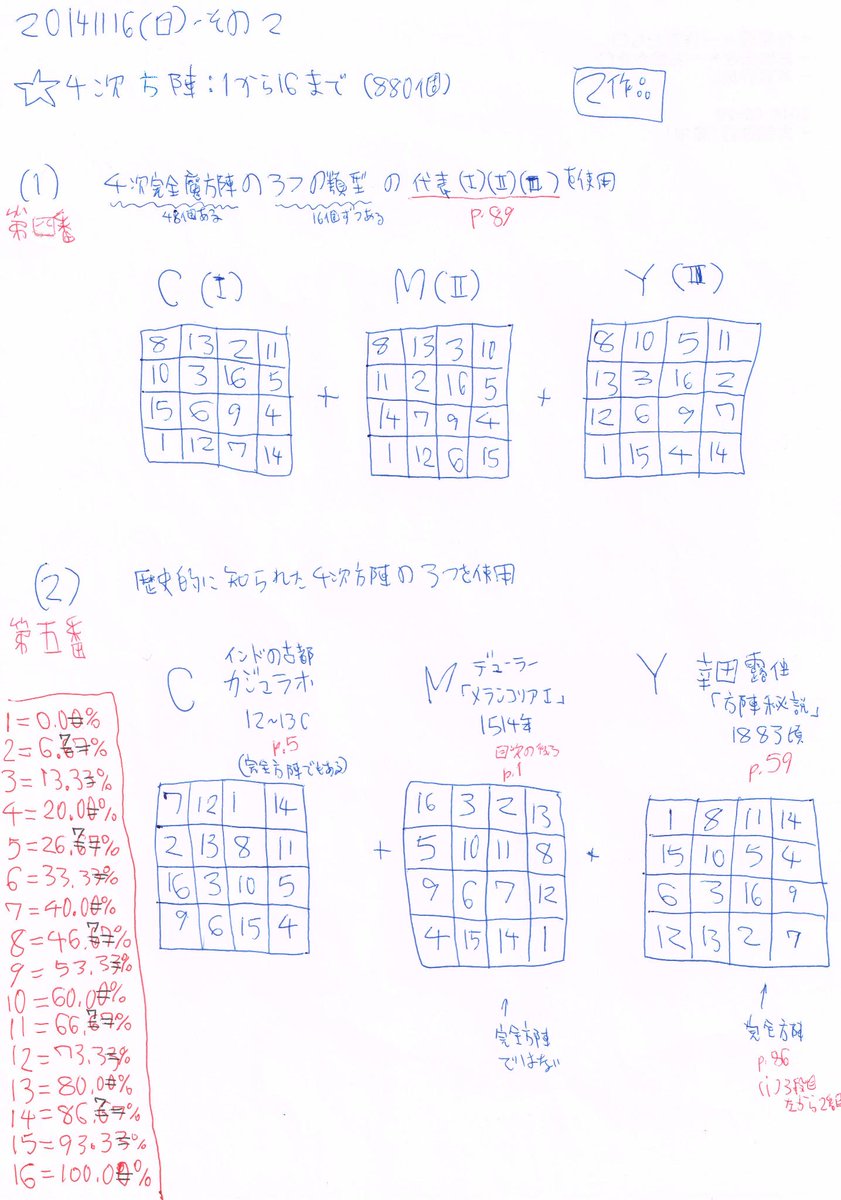 拡大
拡大
 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣第四番 Colored Magic Square No. 4 2014 油彩、キャンバス 1092x1092 4次完全魔方陣の3つの類型の代表1種ずつをC,M,Yに aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣
2014-12-04 06:16:37 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣第五番 Colored Magic Square No. 5 2014 油彩、キャンバス 1332x1332 備考:歴史的4次方陣。カジュラホ、デューラー、幸田露伴 aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣
2014-12-04 06:19:25 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
5次方陣 5x5 Magic Square aloalo.co.jp/nakazawa/2014/… #色彩魔方陣 pic.twitter.com/WiWRzMrrPl
2014-12-04 06:20:36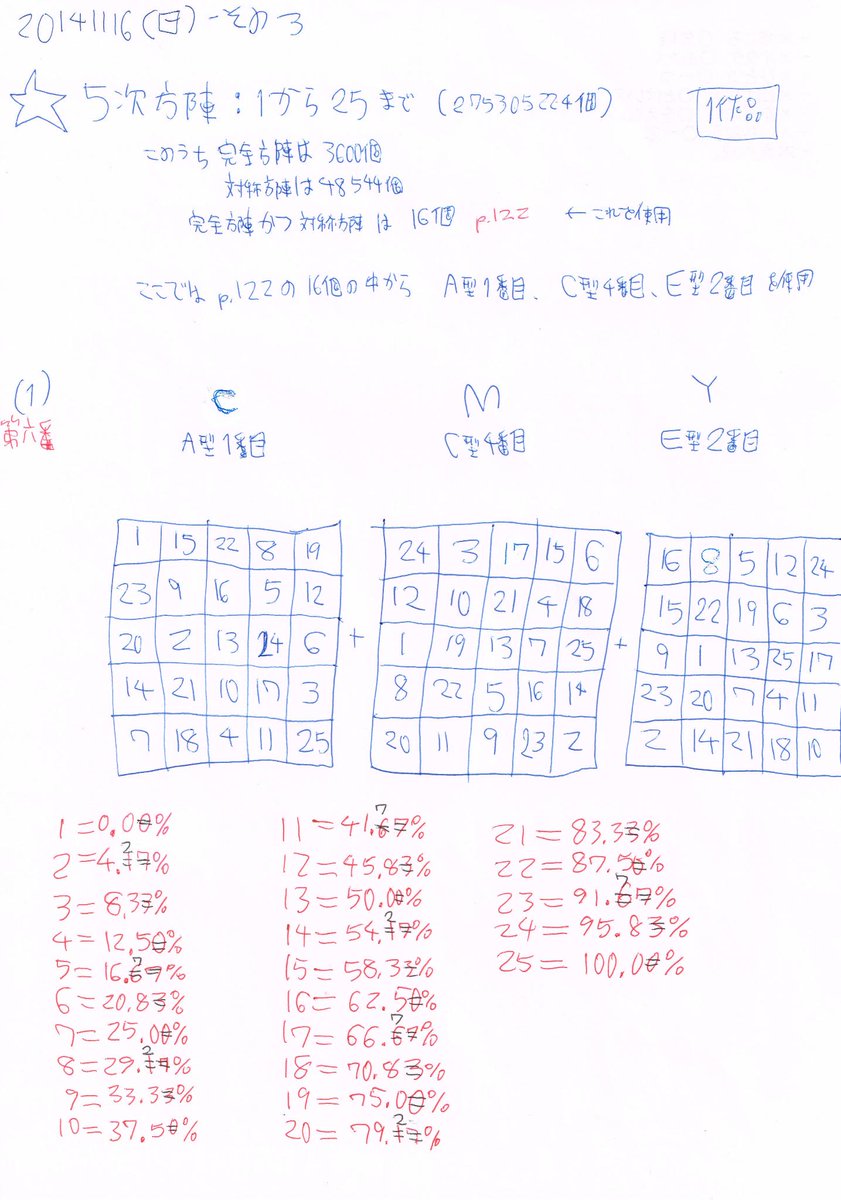 拡大
拡大
 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣第六番 Colored Magic Square No. 6 2014 油彩、キャンバス 2050x2050 備考:5次方陣。完全かつ対称方陣は16個。その中の3種 aloalo.co.jp/nakazawa/2014/… aloalo.co.jp/nakazawa/2014/… #色彩魔方陣
2014-12-04 06:23:10 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
3x3の方陣ではインクの0%から100%までを1から9の9段階に対応させるため12.5%ずつとなる。 各行各列とも各色インク総量は150%となる。各マス平均50%x3ということ。 中央マスが「C50% M50% Y50%」なのでその両端は補色の関係。 #色彩魔方陣
2014-12-04 06:24:10 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
4x4の方陣ではインクの0%から100%までを1から16の16段階に対応させるため6.666...%ずつとなるが四捨五入している。 各行各列とも各色インク総量は各マス平均50%x4=200%となるはずだがそのまま計算すると四捨五入のせいで0.1%ずれたりしている。 #色彩魔方陣
2014-12-04 06:24:44 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
880個ある4x4の方陣から数学的必然により3つを選んで第四番を作った。48個の完全方陣の3型(各16個ずつ)のうち左下に1が来るものをC,M,Yの3つとして選んだため右上から2番目のマスがどれも16になるなど全体的に似た形なため全体的にグレーっぽくなった。 #色彩魔方陣
2014-12-04 06:25:05 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
880個ある4x4の方陣から文学的ウンチクにより3つを選んで第五番を作った。Cはインドの古都カジュラホの12世紀の遺跡にあった方陣。Mはデューラーが1514年にメランコリアIに描き入れた方陣。Yは幸田露伴が1883年に方陣秘説で紹介した方陣。年代順、印欧日。 #色彩魔方陣
2014-12-04 06:25:23 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
5x5の方陣ではインクの0%から100%までを1から25の25段階に対応させるため4.166...%ずつとなるが四捨五入している。 各行各列とも各色インク総量は各マス平均50%x5=250%となるはずだがそのまま計算すると四捨五入のせいで0.1%ずれたりしている。 #色彩魔方陣
2014-12-04 06:25:45 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
2億7千万個ある5x5の方陣から数学的に3つを選んで第六番を作った。完全方陣は3600個、対称方陣は4万8千個たが完全方陣かつ対称方陣だとたった16個。ここからの3つをC,M,Yに適用。色彩魔方陣の性格に完全方陣と対称方陣の性格が加味され非常に整合性がある。 #色彩魔方陣
2014-12-04 06:26:11 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
色彩魔方陣の性格とは、ひとつの行の中に等量のCインク、Mインク、Yインクが盛られているすなわち混ぜれば完全に50%ずつのグレーとなること。ひとつの列の中でも同様。完全方陣の性格とは、それが45度の対角線のみならず、対角線に平行なすべての45度線でもそうであること。 #色彩魔方陣
2014-12-04 06:26:31 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
対称方陣の性格とは、中央マスを中心として点対称位置にある任意の2つのマスのCインク、Mインク、Yインクの和がそれぞれ100%となること。ということは、第六番においては点対称位置にある任意の2つのマスはすべて補色の関係となっているということ! #色彩魔方陣
2014-12-04 06:26:46 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
このように第六番においては25マスの色彩が非常に整合性のあるものとなっている。数学的に美しい。ゆえにわれわれは、美学的にもこれを美しいと感じなければならない。・・・かどうかはまた次の話。だがその「次の話」に行く直前までは定量的にきちんとやりましたよ、という話。 #色彩魔方陣
2014-12-04 06:27:05 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
さてモノクロの数値が「作品」で、カラーの出力が「参考」であることについて。プリンタによって発色が異なるという理由の他に、ギリシャ哲学ならば前者はイデア、後者は物質。HTMLならば前者はソース、後者は実行。記号論なら前者はシニフィエ、後者はシニフィアン。等。 #色彩魔方陣
2014-12-04 06:27:36 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
しかし最も整合性のある説明は、理想的なCインク、Mインク、Yインクが存在不能だから。現実界では「C100% M100% Y100%」は黒にならない(なので実際の印刷ではCMYのほかにKを使用する)。だがイデア界では3原色の数値だけですべての色を表現できる。 #色彩魔方陣
2014-12-04 06:27:56 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
ここで復習。ヒトの場合網膜錐体細胞が3種あるため3原色となる。色光の3原色はRGB(加法混色/デフォルト黒)。色素の3原色はCMY(減法混色/デフォルト白)。モニタだったらRGBだが、絵画は白キャンバスがデフォルトで絵の具という色素の体系なためCMYが正解。 #色彩魔方陣
2014-12-04 06:28:13 中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
中ザワヒデキHidekiNAKAZAWA
@nakaZAWAHIDEKI
もうひとつ復習。印象主義の理論は筆触分割と色彩分割。方法主義において筆触分割は画素の多数性、色彩分割は画素の多種性へと抽象化された。本作において画素の多数性は魔方陣のグリッドとして、画素の多種性はCMYの数値の差異として実現。すなわち誠に今日的な印象主義絵画を自任。 #色彩魔方陣
2014-12-04 06:28:39