鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
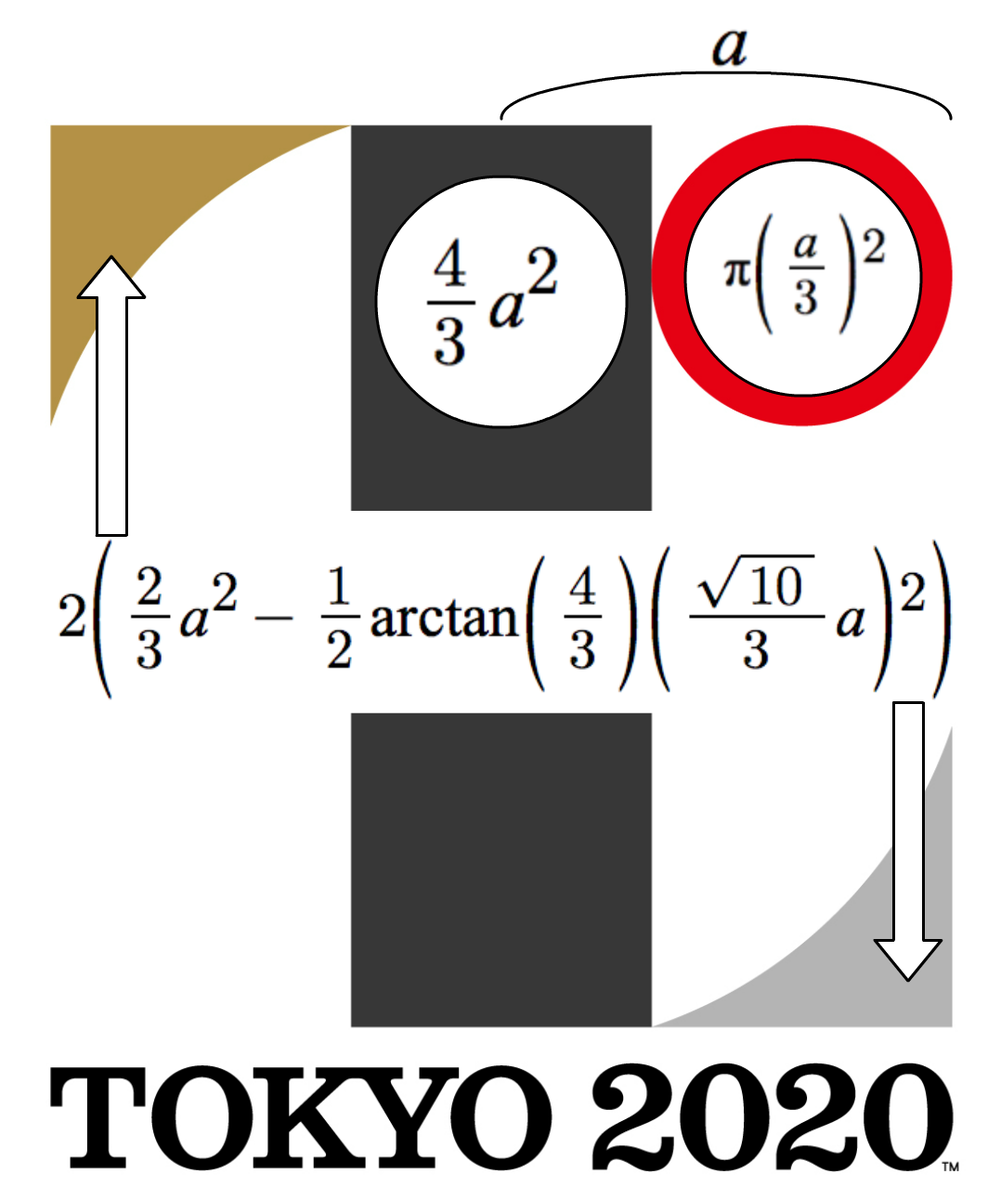
カッコイイと話題の東京五輪エンブレムの面積を求めようとしてたら途中で三角関数地獄に突入してわけがわからなくなったので、とりあえずエンブレムを描く方程式だけはつくってみたぞ(aは一番外側の正方形の内接円の半径=一辺の半分) pic.twitter.com/omrVeDVJqI
2015-07-25 22:59:15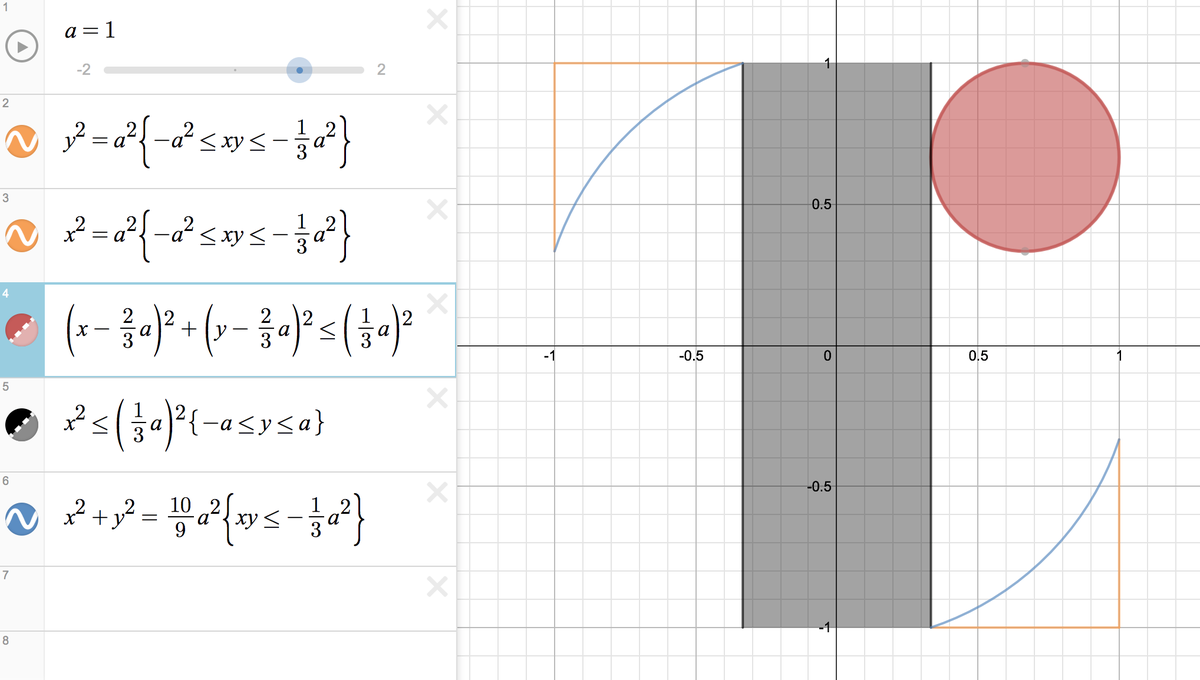 拡大
拡大
 鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
右上の丸と真ん中の海苔はいいんだよ。問題は左上と右下のやつ。ここにはまさかのタンジェント地獄がひそんでいた
2015-07-25 23:08:17 鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
@Natrium_exe じゃああってるんでないかな なんかもっと簡単な方法ある気がしないでもない
2015-07-25 23:37:38 鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
こうやってそれぞれの面積を出して、それを全部足して、最後にちょっと整理したのがさっきの式です pic.twitter.com/XU8pG6iDMG
2015-07-26 13:37:22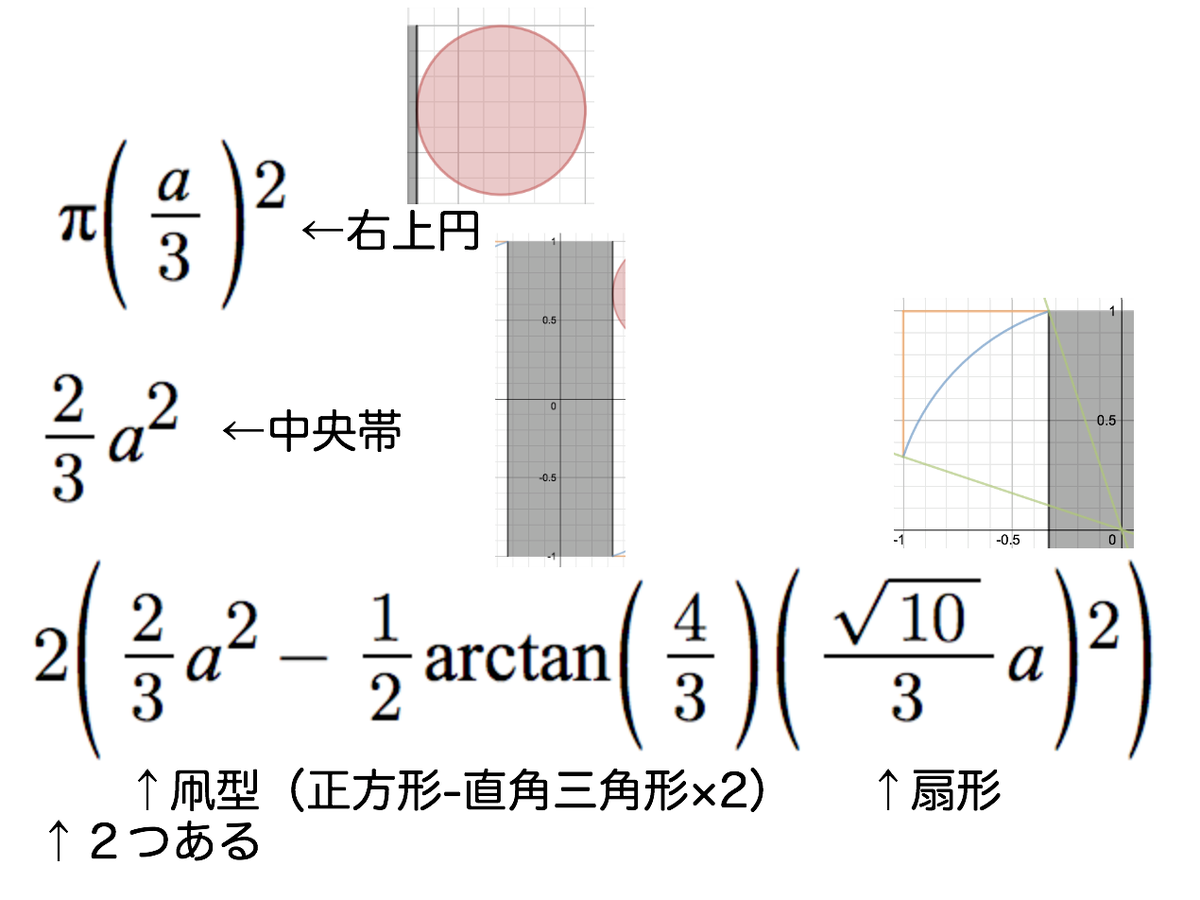 拡大
拡大
 鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
鯵坂もっちょ🐟『つれづれなる数学日記』発売中
@motcho_tw
「pi」も「arctan(4/3)」も定数なんだからただの数として書けばもっとわかりやすくなるよな。 ということで東京オリンピックのエンブレムの面積は外側の正方形の一辺の半分がaのとき1.9854a^2だ
2015-07-26 23:50:22