【数学】花火の音が聞こえない場所はできるか問題

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

花火大会の開催位置と花火の聞こえる限界距離を与えれば都内で花火の音の聞こえないポイントが割り出せるだろうか

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

東京23区を半径30kmの円で覆い尽くすには最低何箇所で花火大会を開催しなければならないか問題　とかどうかな

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

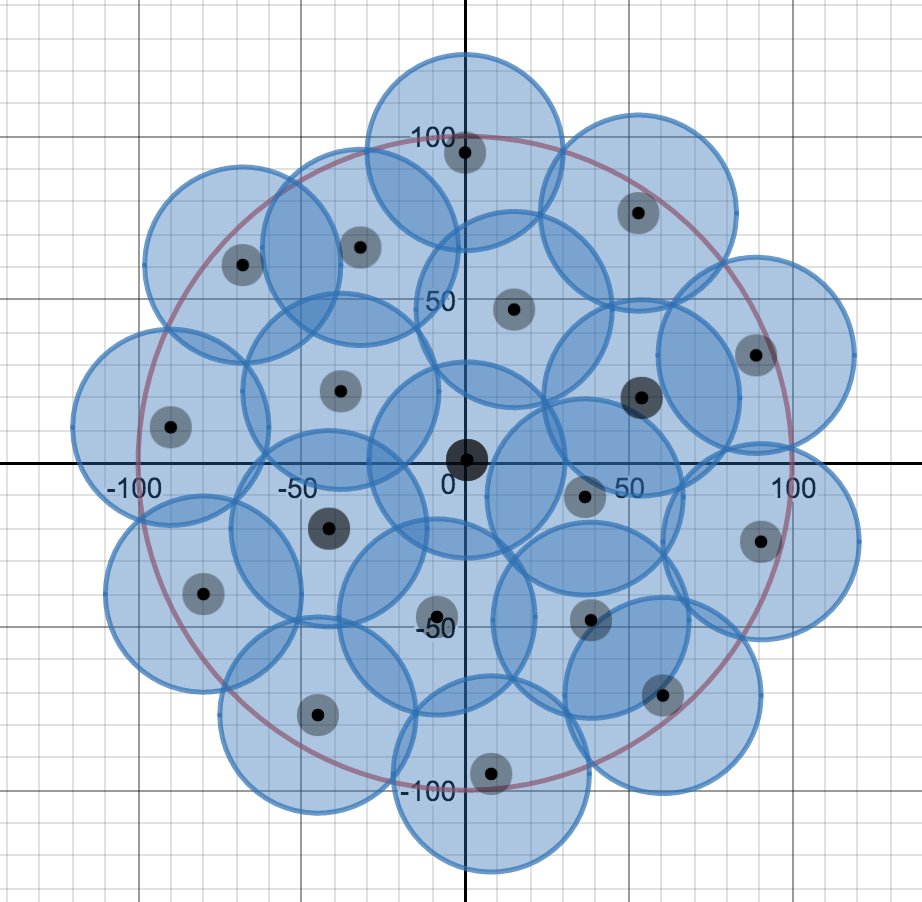
C県は半径100kmの円である。花火の音は30km先まで届く。C県内の花火大会だけでC県全域に花火の音を行き渡らせるには、最低何箇所で花火大会を開催しなければならないか。

□ @dafuyafu

東京都はコンパクト空間だった！！？

名無し.exe @Natrium_exe

下界は自体は100^2/30^2だから最低12箇所だな

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

@Natrium_exe ふぉ！なんでそうなりました？

名無し.exe @Natrium_exe

@motcho_tw 面積比。半径30kmの円で埋め尽くすならその面積の総和はC県の面積以上になる

名無し.exe @Natrium_exe

ただ、12箇所設置すれば埋め尽くせるかどうかは別

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

@Natrium_exe 半径30kmの円が12枚あれば面積的には半径100kmの円の面積を超えるけど、実際に小円を12個並べて大円を覆い尽くすことは可能？

名無し.exe @Natrium_exe

@motcho_tw まぁ無理だと思う。だから下界なんだけど

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

@Natrium_exe ああそういうことか

あるみ @alumi_mikan

@motcho_tw 携帯のセルラー方式に通ずるところがありそうですね

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

@misoxjp たしかに

タカピコ @takapiko

携帯の基地局とかってこういうこと考えて場所キメてるんだろうなぁって思った

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

C県、岩手県より広いじゃねえか

名無し.exe @Natrium_exe

おそらくC県の中央では開催しないと思う。中央で開催すると直径を埋めるのに5箇所いるけど、直径自体は4箇所で埋められる

名無し.exe @Natrium_exe

あと、円同士が接するような埋め方はしないんじゃないかという気はする

名無し.exe @Natrium_exe

あ、しないわ

名無し.exe @Natrium_exe

ん、しなくもないか？

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

美しくない（23箇所） pic.twitter.com/ftxAtbuV6W

拡大

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

21箇所まで減らせたけどやってることが全然数学じゃない pic.twitter.com/ACzT6hbxqi

拡大

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

ボロノイ分割っぽいな

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

19 pic.twitter.com/mZeZFBLHxS

拡大

たいしょー @garzbid

@motcho_tw 突然すいません。円を正六角形に変えて敷き詰める問題にかえてみると19であることが直感的にすぐ出てくると感じました。何か数式でうまく書ける方法考えてます笑

鯵坂もっちょ🐟『つれづれなる数学日記』発売中 @motcho_tw

まじか