松丸 亮吾 🍥
@ryogomatsumaru
松丸 亮吾 🍥
@ryogomatsumaru
謎解き・脱出ゲームを考案するクリエイター。謎解きの世界大会で優勝し、世界一になりました…!🥇 ポケモン/ボカロが大好き。相棒は保護猫のリドくん🐈 会社 → @riddler_nazo
 松丸 亮吾 🍥
@ryogomatsumaru
松丸 亮吾 🍥
@ryogomatsumaru
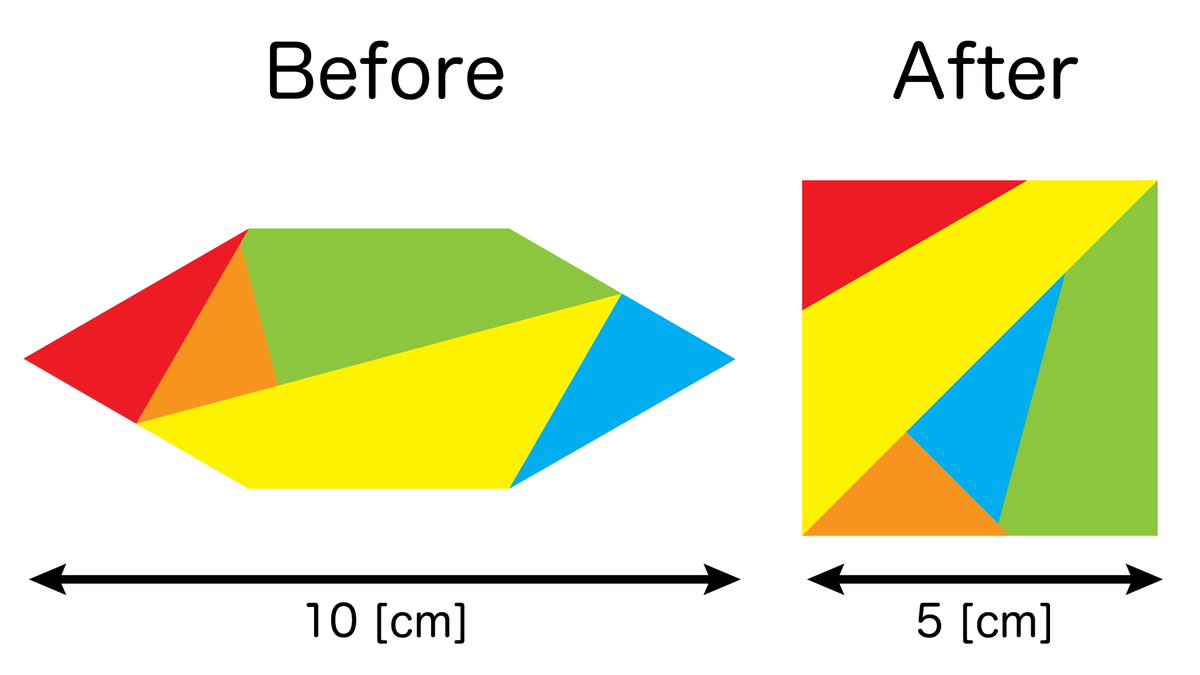
小3のときに作った算数の問題です。 小学校で習う知識だけで解けます、ルートも使いません。ぜひやってみてね。 pic.twitter.com/5k1rxYzyvF
2019-01-07 21:52:15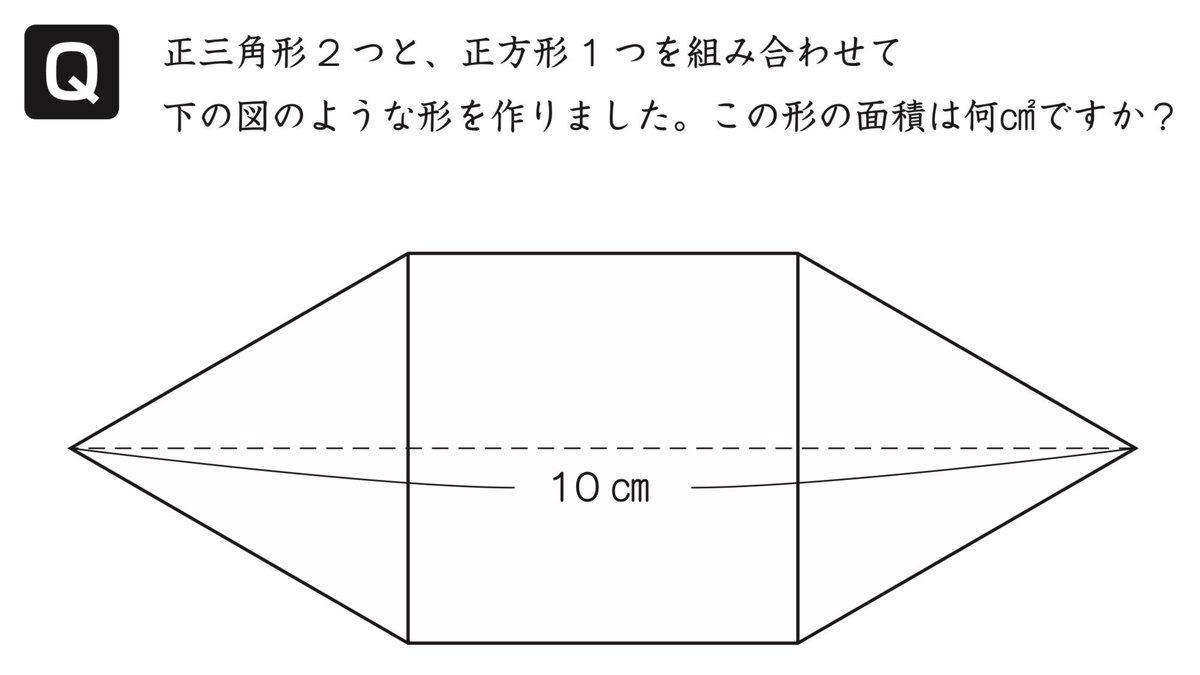 拡大
拡大
 松丸 亮吾 🍥
@ryogomatsumaru
松丸 亮吾 🍥
@ryogomatsumaru
リプライを見ている感じ、28㎠という誤答が多そうですね…🤔 正三角形の高さは綺麗な整数にはならず、それを求めようとするとルート計算を避けて通れません。 逆に言えば、正三角形の高さが求められなくても、全体の面積は出せるということです。
2019-01-07 22:39:31 TOMO
@TOMO_dotty
TOMO
@TOMO_dotty
んー、台形の求め方でいいんじゃないかな?正方形の辺が10/3cmだから高さは更に半分の5/3cmで、上下あるから台形公式の最後の割る2を省けば良いのかな? てことで50/3cm2? twitter.com/ryogomatsumaru…
2019-01-08 11:05:05 つだきち謎検3級
@Tsudakichi1977
つだきち謎検3級
@Tsudakichi1977
三角形の特性で正三角形を同じ高さの直角三角形に直して……、わからん! twitter.com/ryogomatsumaru…
2019-01-08 10:48:42 🦀QuestCrab🦀
@fuchikoma1977
🦀QuestCrab🦀
@fuchikoma1977
小学校時代を思い出し、直感で50。後で確認しよう。 twitter.com/ryogomatsumaru…
2019-01-08 10:44:09 松丸 亮吾 🍥
@ryogomatsumaru
松丸 亮吾 🍥
@ryogomatsumaru
ちなみに合ってるかどうかのチェックをしたい方のために答えの数値のヒントを言うと、 答えは「2で割り切れない整数」になります。整数にならなかった方、2で割り切れる値になった方は、何かを間違えています。 あきらめずに挑戦してみてね。
2019-01-07 22:41:39 えったん
@ettan_pf88
えったん
@ettan_pf88
@ryogomatsumaru お返事ありがとうございます! 本やテレビなど、すごく楽しく見させてもらっています。中学校の数学教師です!! 中3までの数学で解くことはできたので、算数での解き方を考えています。自分の中でスッキリできたら、冬休み明け、中2の生徒達にも授業の中で出してあげようと思います(*^^*) 難しい…
2019-01-07 23:40:36 松丸 亮吾 🍥
@ryogomatsumaru
松丸 亮吾 🍥
@ryogomatsumaru
@ettan_pf88 おお、嬉しい…!! 算数の解き方の場合、計算自体は単純な式1つで終わるのでスカッとするはずです…!ぜひがんばって!
2019-01-07 23:43:35 えったん
@ettan_pf88
えったん
@ettan_pf88
@ryogomatsumaru 解けた!解けました!! 松丸くん、 いい年始をありがとぉー!! (о´∀`о) やっと寝られる(笑)
2019-01-08 02:20:56