早野龍五先生・宮崎真先生の第一論文も間違いでは?の巻
-
- いいね！0
Yoh Tanimoto
@yoh_tanimoto
早野さん @hayano は70年の累積線量を 60mSv としたのだとすると、どうやって計算をしたのでしょうか? もしかして、[2]第一論文の手法による結論である c^A が 3倍だったのでしょうか?
2019-01-09 08:00:32
Yoh Tanimoto
@yoh_tanimoto
これはおかしいです。"見解"によると、70年の累積線量は 60mSv 程度のはずです。どこで計算を間違ったのでしょうか? 累積線量は H_{10}^{Ai}(0.65) と f(t) と c^A がわかれば後は積分するだけです。前の 2つはガラスバッジとは関係がありません。c^A は第一論文の手法で計算されたはずです。
2019-01-09 08:00:05
Yoh Tanimoto
@yoh_tanimoto
計算したものがこちらです。 wolframalpha.com/input/?i=plot+… 横軸の単位は月ですから、70年は840ヶ月で、5ヶ月めからのそこでの累積線量は15.4mSv 、生涯の累積線量はそれに初期被爆 I = 1.5mSv を足した 16.9 mSv となります。もとの論文の 18mSv はこれに近いですね。横軸年では wolframalpha.com/input/?i=plot+…
2019-01-09 07:59:42
Yoh Tanimoto
@yoh_tanimoto
あとは式(2)で残っているのは c^i です。これは、空間線量率とガラスバッジの線量率との係数 c を決めた第1論文の手法を使って出されたもので、第2論文では、 Zone A では c^A = 0.10 であるとされています。これですべての材料がそろったので、式(2)の積分が計算できます。
2019-01-09 07:59:19
Yoh Tanimoto
@yoh_tanimoto
式(2) に戻ると、まだ初期 4ヶ月の被爆 I があります。これは今回の"見解"では触れられていないので論文のままです。図5-1 を見ると、 5ヶ月めのところでグラフが 1.5mSv くらいで始まっているので、I はこれと同じか少し小さい値になります。あまり影響はないので I = 1.5mSv としておきましょう。
2019-01-09 07:59:02
Yoh Tanimoto
@yoh_tanimoto
その他にいろいろ定数がありますが、これらはセシウムの半減期だったり、放射性セシウムの比だったり、3.1節にあるように空間線量から決められるものなので、ガラスバッジとは関係がありません。よって f(t) は計算できて、こうなり、 wolframalpha.com/input/?i=plot+… 図2と合っています。
2019-01-09 07:58:44
Yoh Tanimoto
@yoh_tanimoto
この 18mSv というのは論文の図6,7 のデータとは関係がありません。これを計算するためには式(2)の積分をすればよいのです。式(2)直後に書いてあるように、H_{10}^{Ai}(0.65)=2.1uSv です。f(t)は(1)に書いてありますが、本当はこれを規格化しないといけません。 twitter.com/hyd3nekosuki/s…
2019-01-09 07:58:29
Yoh Tanimoto
@yoh_tanimoto
[1]の70年の累積線量評価というのは、修正前の論文 iopscience.iop.org/article/10.108… に書いてある 18mSv のことのはずです。報道 www3.nhk.or.jp/news/html/2019… によると 3倍して 50-60mSv になるはずということなので、これの 1/3 ということで合っています。
2019-01-09 07:58:10
Yoh Tanimoto
@yoh_tanimoto
早野さんの見解 twitter.com/hayano/status/… ぼくが勘違いしていなければ、とても驚くべきことが書いてあるので、よく考えてみましょう。ここでは [1]70年の累積線量計算を1/3に過小評価していた [2]第一論文の結論に誤りはない、という 2つのことが主張されています。
2019-01-09 07:57:53
ryugo hayano
@hayano
本日1/8，文科省記者クラブに「伊達市⺠の外部被ばく線量に関する論⽂についての⾒解」を貼出いたしました．70年間の累積線量計算を1/3に評価していたという重大な誤りがあったことと，その原因，意図的ではなかったこと，今後の対応，伊達市の方々への陳謝などを記したものです→ pic.twitter.com/OuHJKXZmY2
2019-01-08 13:05:14
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
早野先生 @hayano 本日の見解での御説明、測定データの累積についても成立していないのではないでしょうか？ Fig. 6で線量率の中央値をグラフから読み取って、24時間*30日をかけて28ヶ月まで累積すると1.7mSvにしかならず、Fig. 7の下位1/4以下になります。御説明と論文のデータが一致しないのでは？ pic.twitter.com/oS06pEU3la
2019-01-08 22:46:03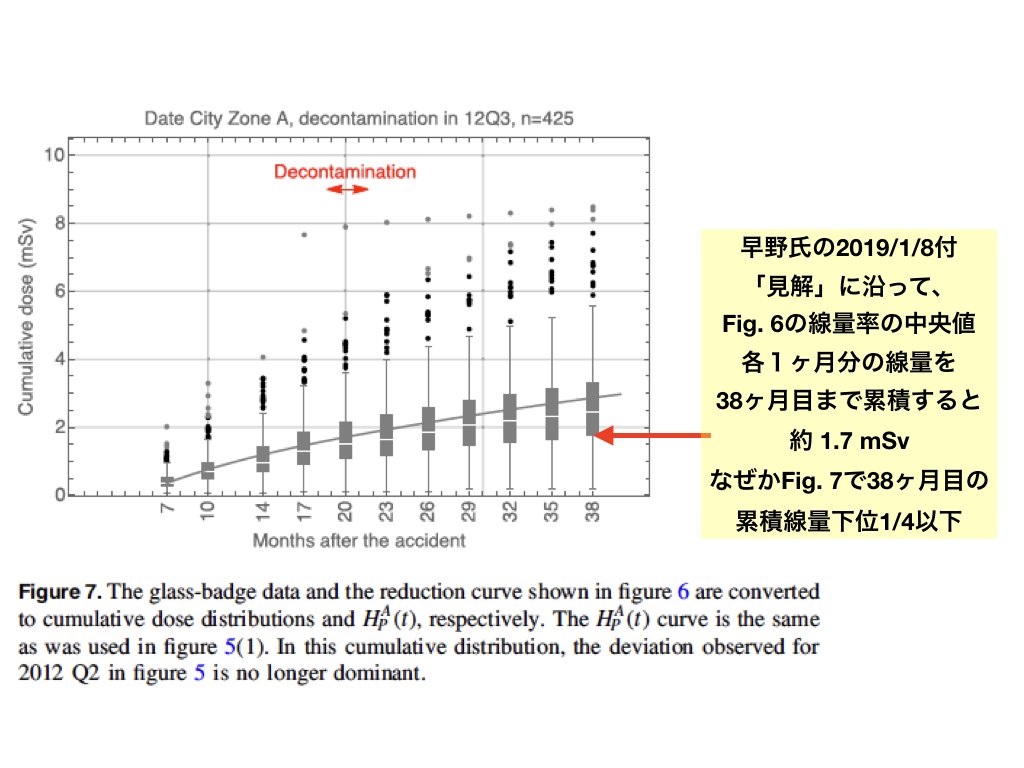
拡大
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
Fig. 7の曲線はどのようにして決定したのか、また「見解」にある「曲線の積分式にも同様な誤りがあり」とはどのような誤りだったのか、ご説明頂けますでしょうか？
2019-01-08 18:08:17
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
- Fig. 6の脚注では微分値 \dot{H}_p が(上付きAがないのはtypoでしょうか?) について"hence contains no adjustable parameters" とまで述べているのでFig. 7では同じパラメータでの積分値を理論式として用いるのが自然かと思いますが、もしそうしていればFig. 7の曲線になりません。
2019-01-08 18:08:17
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
- この曲線は(2)式で与えられていて、式中の積分をする際に3ヶ月ごとに分割して、それを１ヶ月のものと取り違える、のような誤りが発生するステップは存在しないはずです。
2019-01-08 18:08:16
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
早野先生 @hayano 「見解」を拝見しましたが、十分な説明にはなっていないと思います。 - ガラスバッジ線量の累積計算で3ヶ月分を1ヶ月に取り違えたということは（あってはならないものの）まだ理解できます。 - しかし、「曲線の積分式にも同様な誤り」は常識的に考えられないのではないでしょうか？ twitter.com/hayano/status/…
2019-01-08 18:08:16
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
細かい整合性を積み上げが科学ですから、整合性のない論文は科学的成果とは言えない。従って、「一般人」の方も、そのような論文の主張を「科学的」とみなしてはいけない。ましてや、大多数の生活に影響する政策の根拠にするのは論外です。（なお、既に「細かい」というよりも派手な不整合ですね。） twitter.com/BugbearR/statu…
2019-01-06 15:21:11
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
私も全く同意です↓ twitter.com/MasakiOshikawa… Fig. 7 だけ修正すれば良いという類の問題ではなく、論文の信頼性に重大な疑義が生じるレベルの不整合です。 twitter.com/yoh_tanimoto/s…
2019-01-06 15:07:45
Masaki Oshikawa (押川 正毅)
@MasakiOshikawa
（承前）しかし、ここで触れたFig. 6→Fig. 7だけでも宮崎・早野論文のデータおよび解析の信頼性には重大な疑念が生じます。さらに、これに限らず他にも多数の不整合があるようです。従って、宮崎・早野論文を根拠に帰還政策等を論じることはできないでしょう。
2019-01-01 18:17:04
Yoh Tanimoto
@yoh_tanimoto
@MasakiOshikawa その通りです。Fig. 6 は c^A=0.15 なら合うのですが、 Fig. 7 は c^A = 0.10 でも合いません。最後の t=70y での累積線量は c^A = 0.10 で計算するとほぼ合います。どれか一つの図や計算が間違っているというより、論文全体で整合しない点が多すぎる、というのが問題だとぼくは思います。
2019-01-05 01:23:02