LibreOffice CalcとExcelの計算結果誤差をみなさんで検証していただいた結果まとめ

LibreOffice日本語チーム @LibreOffice_Ja

これ、誰か検証していただけませんか? この方が書かれている「結果の信頼性はExcelに分があるように思う」も、なぜそう思われたのか理由も含めて調べるには時間がかかりそうなので（中の人は数学苦手…） twitter.com/haou13fri/stat…

寿限無 @haou13fri

一般項によりフィボナッチ数列を計算すると、LibreOffice Calc では、ちょうど25番目で本来の結果とのずれが生じた。しかしExcelだとExcel2000と2019で試したが、いずれも結果にずれは生じなかった。

2019-06-17 13:15:12

寿限無🍮 @haou13fri

一般項によりフィボナッチ数列を計算すると、LibreOffice Calc では、ちょうど25番目で本来の結果とのずれが生じた。しかしExcelだとExcel2000と2019で試したが、いずれも結果にずれは生じなかった。

寿限無🍮 @haou13fri

方法。セルA1に1、B1に数式 =(((1+SQRT(5))/2)^A1-((1-SQRT(5)/2)^A1)/SQRT(5) を入れる。A2に2、B2はB1のcopyを入れ、A3とB3以下は上からドラッグする。

寿限無🍮 @haou13fri

結論。やはりそれぞれのOfficeソフトウェアに一長一短があるので、使い分けるしかない。一方は他方の代わりにはならない。結果の信頼性はExcelに分があるように思う。

bug @hiddenbugs

@LibreOffice_Ja LibreOffice 6.4 nightly(x64), Excel 2016 で =1/SQRT(5)*(((1+SQRT(5))/2)^A1-(((1-SQRT(5))/2)^A1)) は共にA1が25のとき75025になりました。 なお、式はWikipediaを見ながら修正しています。 1/SQRT(5)が乗算されていなかったのと、 (1-SQRT(5))/2ではなく(1-(SQRT(5)/2))となる式になっていた

K.Shirakata @argrath

@hiddenbugs @LibreOffice_Ja 75025になっているセルの書式設定で小数点以下15桁とかにするとLibOは10桁目に1が出てきますね。Excelは0です。

bug @hiddenbugs

@argrath @LibreOffice_Ja こちらでも再現しました。>1が出てきますね。

K.Shirakata @argrath

LibOの実数演算で誤差が出るやつ、出ること自体は仕方ないにしても小数点以下15桁とか表示させたときに10桁目に誤差が出てしまうのはちょっといけてないな…。long doubleで扱うべきところがどこかでdoubleになってるとかなんだろうけど。

K.Shirakata @argrath

まあ実数演算の誤差のやつはp5pでもよく話題になってるし難しいよなあ…。

いさな @jo3emc

@hiddenbugs @argrath @LibreOffice_Ja Excelは手元になくて比較できませんが、LibOの状況は再現しました（Win7 32bit）。（haou13friさん例示の数式は転記ミスの模様。） 余談ながらTclとPythonでも試してみたところLibOと概ね同じ挙動でした。Cは今環境がなくて試せてません。要は2進数の丸めの扱いですね…。 pic.twitter.com/UwgNZ8kxVC

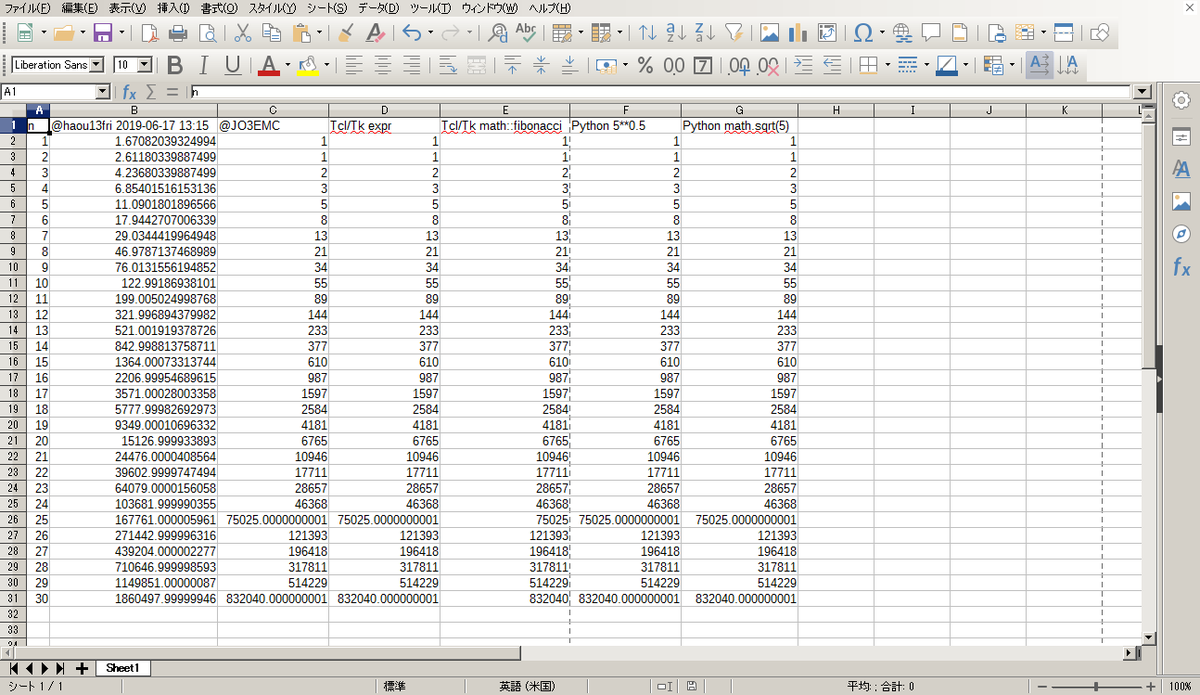拡大

いさな @jo3emc

@hiddenbugs @argrath @LibreOffice_Ja 逆に言うとExcelで整数値が帰ってくる方がおかしいとも…？ あるいはDecimal計算がデフォルトになってるのか…。

Chuui @es_chuui

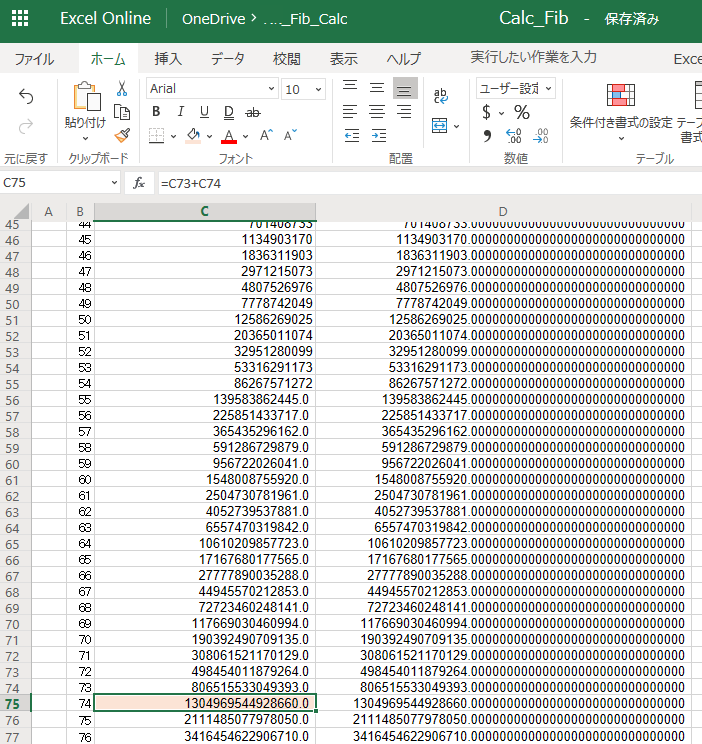
@jo3emc @hiddenbugs @argrath @LibreOffice_Ja Excel Onlineで試してみました。確かにn=25でも誤差が生じないです。n=74で漸化式計算側も精度の情報落ちが生じますが、逆にいうとn=1～73まで正しく整数で答えが出ていることが確認できました。(確認のため小数点以下を30桁表示しました。実際の内部の演算精度はそこまでないと思いますが。) pic.twitter.com/5oU7uHDZuy

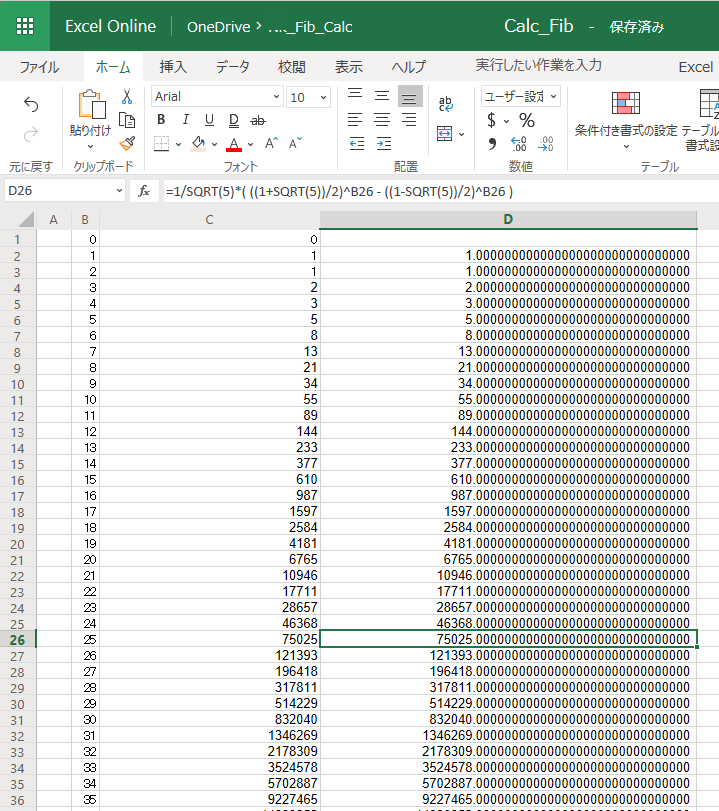拡大

拡大

Chuui @es_chuui

@jo3emc @hiddenbugs @argrath @LibreOffice_Ja (考察1) 一般に浮動小数点の演算はIEEE754の規格を使う。 多くのプログラム言語では倍精度(64bit)を使うが、他にも倍々精度・拡張精度・拡張倍精度が定義されており、IntelCPUのFPUは対応している。Excelはそれを使っているのか？ (考察2) 数式処理で、なるべく誤差がでない計算をしているのか？ 続く

Chuui @es_chuui

@jo3emc @hiddenbugs @argrath @LibreOffice_Ja (考察3) 独自の浮動小数点のフォーマットをプログラム用意する方法とか？ だが、FPUが対応していない浮動小数点書式を扱うのは、さすがに演算速度が厳しいのでは？(整数ならともかく) (考察4) IEEE754(浮動小数)の丸め指定で、なるべく端数がでないのを選んでいるとか？ う～む、詳しい方教えて！

中澤 港％人類生態学者＠神戸大学 @MinatoNakazawa

浮動小数点演算の丸め誤差が出ない方が特殊な処理だと思う。Rで A <- 1:25; B <- (((1+sqrt(5))/2)^A-(((1-sqrt(5))/2)^A))/sqrt(5); C <- numeric(25); C[1] <- 1; C[2] <- 1; for (i in 3:25) { C[i] <- C[i-2] + C[i-1] }; B==C とやると4項目からFALSE twitter.com/LibreOffice_Ja…

中澤 港％人類生態学者＠神戸大学 @MinatoNakazawa

確かにoptions(digits=20); Bとやると，4項目が3.0000000000000004となっている。25項目は誤差が5e-11を初めて超える項。ちなみにLibreOffice Calc 6.2.4.2 (x64)では，小数点以下16桁表示で10桁目に1が出るがB=CはTRUEを返す。 pic.twitter.com/YJUKURp4IL

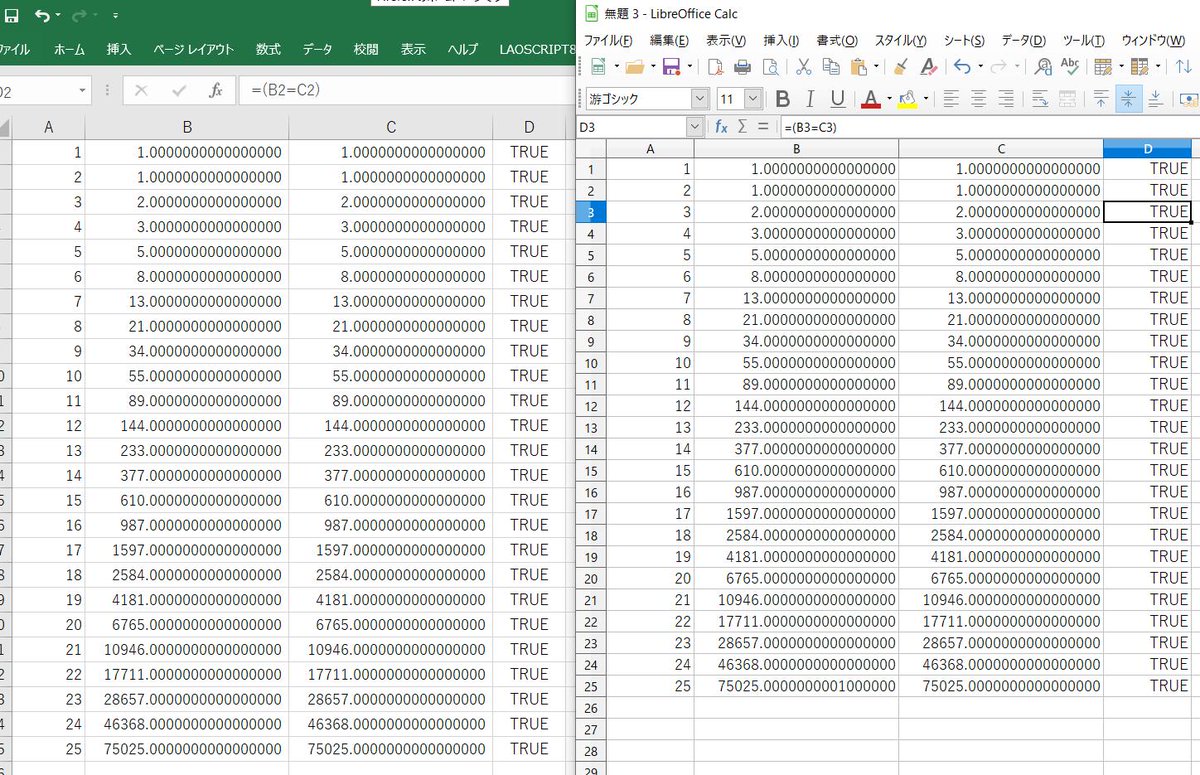拡大

Haruhiko Okumura @h_okumura

昔調べたことですが，Excelの不動小数点演算はおかしな（まずい）ことをしているようです oku.edu.mie-u.ac.jp/~okumura/softw… twitter.com/MinatoNakazawa…

Haruhiko Okumura @h_okumura

「不動」小数点 (^^;;;)

中澤 港％人類生態学者＠神戸大学 @MinatoNakazawa

@h_okumura ありがとうございます。やはりExcelの処理が特殊なのですね

中澤 港％人類生態学者＠神戸大学 @MinatoNakazawa

@LibreOffice_Ja 引用RTでRでの計算結果から，Excelの方が特殊な処理をしているのではないかと書いたら，三重大学の奥村先生がコメントくださり twitter.com/h_okumura/stat… かつて検証されたページを教えてくださいました。