-
 morikuni_net
morikuni_net
- 6173
- 1
- 1
- 3
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
ある人から聞かれたんだけど、オイラーの公式の証明を、三角関数や微分を経由せずに行うのはとても難しい。たまに考えてみるが、ついこれらを使ってしまう。ちなみに、三角関数と微分を前提にすれば例えば、以下のようになる。 #オイラー http://t.co/T6J6yQa
2011-08-16 02:04:08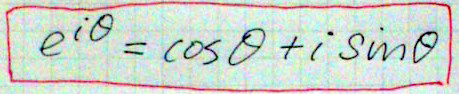 拡大
拡大
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
角Aの回転操作をR(A)と書く。Bだけ回転させた後、角Aの回転をする事はA+Bの回転操作と同じだからR(A)R(B)=R(A+B)。これは指数法則(R^A)(R^B)=R^(A+B)と似ている。いっそR(A)=R^Aと書く。 #オイラー http://t.co/nEX2N3L
2011-08-16 02:14:27 拡大
拡大
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
数字の1は、数直線上の1だけれども、その数直線が2次元平面のx軸だったとして1=(1,0)と表現する。例えば、-1=(-1,0)と書ける。 #オイラー http://t.co/6yHwEee
2011-08-16 02:16:10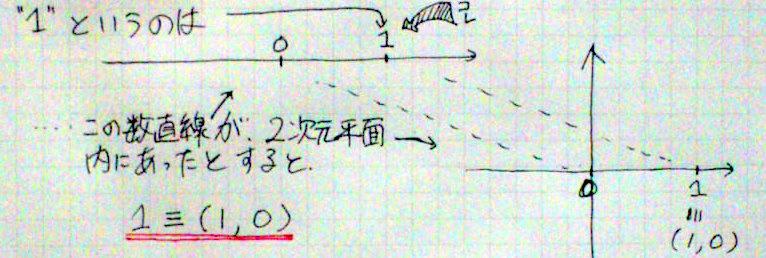 拡大
拡大
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
2次元平面上の座標(1,0)は、π/2ラジアンの回転で(0,1)になる。R^(π/2)の操作を掛け算で表現することにすると、(1,0)=1だったから、(0,1)=R^(π/2)×(1,0)=R^(π/2)×1=R^(π/2) #オイラー
2011-08-16 02:16:59 ぽよ
@Poyo_F
ぽよ
@Poyo_F
(-1,0)は、(1,0)、すなわち1をπラジアンだけ回転したものだから、-1=R^π×(1,0)=R^π×1=R^πとなる。一方R^π=(R^(π/2))^2=-1だから、(0,1)=R^(π/2)=iだ。 #オイラー http://t.co/26mpDye
2011-08-16 02:17:52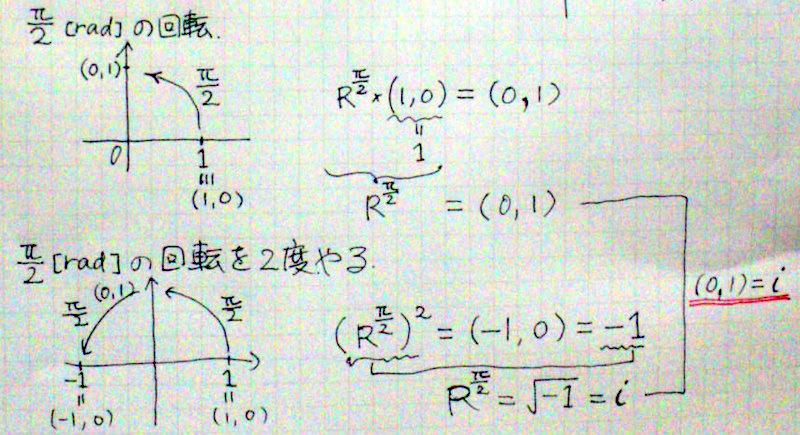 拡大
拡大
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
これまでの議論で、(1,0)=1、(0,1)=iであることが分かった。従って、任意の座標は、(x,y)=x・(1,0)+y・(0,1)=x+yiと書ける。 #オイラー http://t.co/U4IXrfW
2011-08-16 02:25:35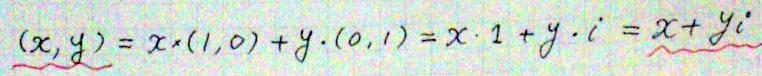 拡大
拡大
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
(x,y)=x+yiと書けるなら、(1,0)を角θだけ回転させた点(cosθ,sinθ)は、cosθ+(sinθ)iと書ける。この点はR^θ×(1,0)=R^θなので、R^θ=cosθ+(sinθ)iと書ける事が分かる。(1,0)=1なので(1,0)が消えた。 #オイラー
2011-08-16 02:35:06 ぽよ
@Poyo_F
ぽよ
@Poyo_F
R^θ=cosθ+(sinθ)iの両辺をθで微分すると、(ln R)R^θ=-sinθ+(cosθ)i=i{i(sinθ)+cosθ}=iR^θなので、ln R=i。但し、「ln」というのは、自然対数の底eを底とするlogの事。 #オイラー
2011-08-16 02:36:10 ぽよ
@Poyo_F
ぽよ
@Poyo_F
ln R=i という事は、R=e^iという事。回転操作は結局R(θ)=R^θ=e^(iθ)と表わされる。つまり、e^(iθ)=cosθ+(sinθ)iと書ける。θ=πを代入すれば、e^(iπ)=-1になる。 #オイラー http://t.co/i2Xeay1
2011-08-16 02:40:56 拡大
拡大
 ぽよ
@Poyo_F
ぽよ
@Poyo_F
(x,y)=x+yiを示す部分を補足します。ここは最初に複素平面を導入するのを避けて、「y軸は虚数軸」とは言わないところがミソです。ベクトルの、和(x,y)=(x,0)+(0,y)と定数倍(0,y)=y・(0,1)で考えた後、(0,1)をiで置き換えるのです。 #オイラー
2011-08-17 00:21:53