-
 zionadchat
zionadchat
- 1144
- 2
- 0
- 0
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
こっから読み始める数学関係者の方には、 ユークリッド幾何学から派生した、 非ユークリッド幾何学の話を連想してもらいたい。
2017-09-15 08:54:37 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
駅ホーム白線原子1つ1つを列車から注目すれば、 ローレンツ収縮は、実験観察から幻想論理であること明白。 カメラアイ位置と白線原子Aとの時々刻々の距離。 カメラアイ位置と白線原子Bとの時々刻々の距離。 この差分から白線原子Aと白線原子B位置の距離は一定。
2017-09-15 08:55:05 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ローレンツ変換は、 数学者が定義宣言する時刻Aとか時刻Bの 「数直線とか平面」を構成する点群を、 カメラアイ局所点実験観察器械(きかい)にとっての 同時刻点群に補正する変換式になる。
2017-09-15 08:56:14 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
アインシュタイン氏の提唱、光速を基準に物理世界を記述するは生きてるが、 電磁現象世界で観察対象の位置とか速度を情報として集める作業過程が抜けているので、 特殊相対性理論仮説は観察対象輪郭線の位置とか速度情報を瞬時に得ることを前提としたガリレオ相対性原理の延長思考方法であり、
2017-09-15 08:57:23 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
光子や原子は、「線路慣性系だ。列車慣性系だ。」に状態分類される以前に存在を措定(そてい)すべき思考対象であり、 座標に物理世界を記述転記する認識者の観察対象慣性系状態分類とは独立に存在するものであり、慣性系ごとに時の流れが異なるというアインシュタイン氏仮説論理も幻想である。
2017-09-15 08:58:05 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
というのが、zionadchat の、主張であり、 慣性系ごとの時の流れが異なることもなく、 ローレンツ収縮もなく、 ニュートンの絶対空間と絶対時間が、 マックスウェル電磁方程式と相性の良いものであり、
2017-09-15 08:58:24 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
その世界構造を知ると、現状の量子力学と親和性が高く、 現状の量子力学を包摂し、その先を示す。 21世紀物理学のパラダイムシフト地図になるというものである。 電磁現象世界の相対性概念、その構造を知れば。
2017-09-15 08:58:47 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
現代数学を知らぬ俺(高校数学もあやしい)ではありますが、 すでに数学者の方々にとっては既に当然の 数学構造の一部であると推察しています。 英(仏)語学習の1人称とか2人称、3人称が関わってくる 相対性の認識空間。或いは、主語なしの世界。
2017-09-15 08:59:07 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
これが法螺話であるかどうか、 まずは、「ローレンツ収縮がない。」 そして、「慣性系ごとに時の異なる流れもない。」 という、現在物理業界主流では認められてない2つを、
2017-09-15 09:00:37 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ユークリッド幾何学に対する非ユークリッド幾何学の公理(法螺話)のようなものとして適用した場合はどうなるか、 以下の話を、暇つぶしに御覧いただけると嬉しい。
2017-09-15 09:00:50 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
走行中の列車床から、身長0メートルの小人が真上に レーザーとかビームを発射したら、真上の天井に穴が開(あ)くのか。 というトリック頓知問題を、いま、やっています。 pic.twitter.com/d4CTO2XbSx
2017-09-15 09:01:44 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
言葉とイメージの誘導に騙されない為に、 左車窓と右車窓に光子ピストルを同時発射して、 列車幅(左車窓から右車窓の長さ)が、 0長さの場合と、 2光秒長さの場合で、 どうなるか、考えてもらっています。 pic.twitter.com/rwJexRFHrZ
2017-09-15 09:02:26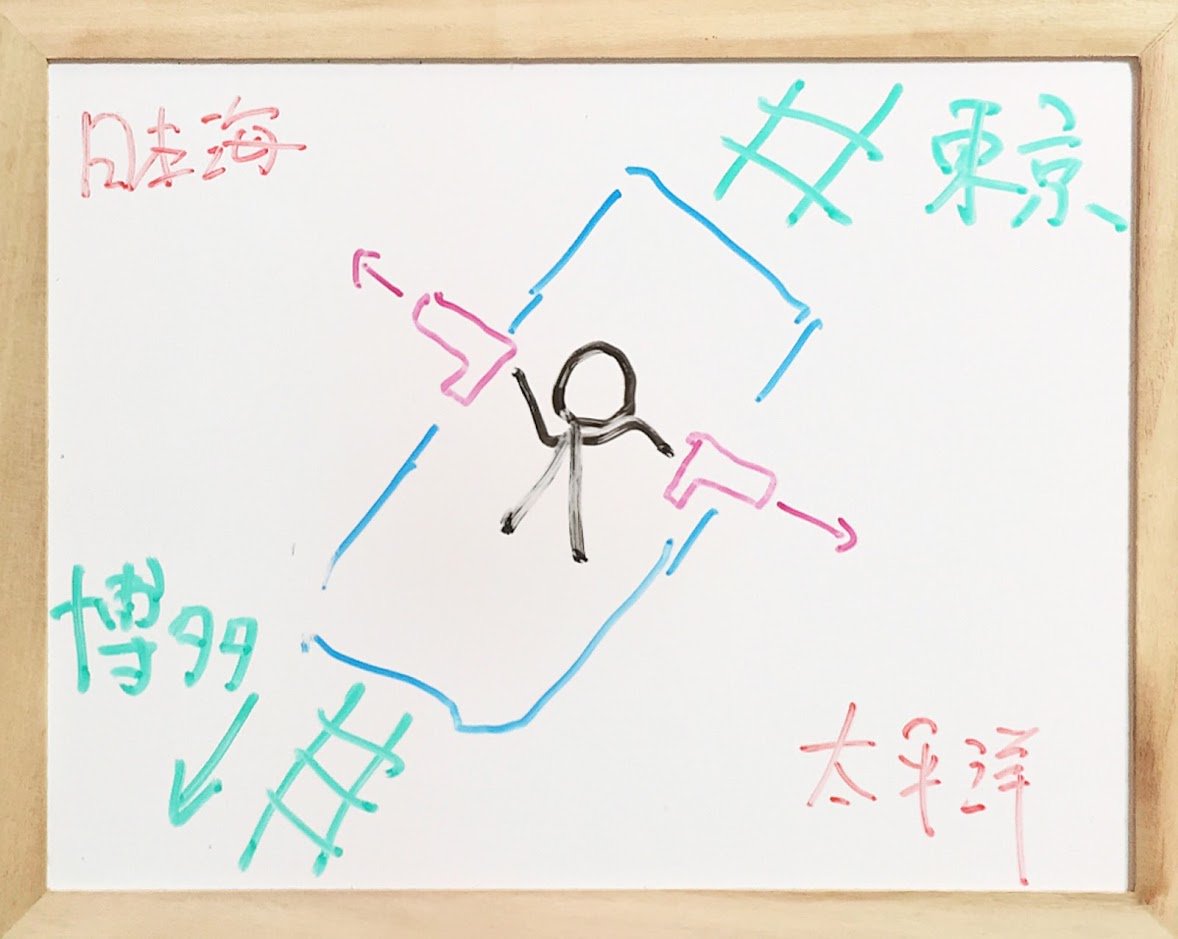 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
映画「アラビアのロレンス」。砂漠での線路破壊。 頭部なしのガンダムを砂漠の線路下に穴掘って、 線路レール下から列車床と列車天井に穴を空けてもらいましょう。 pic.twitter.com/tvA4wpa2bO
2017-09-15 09:03:05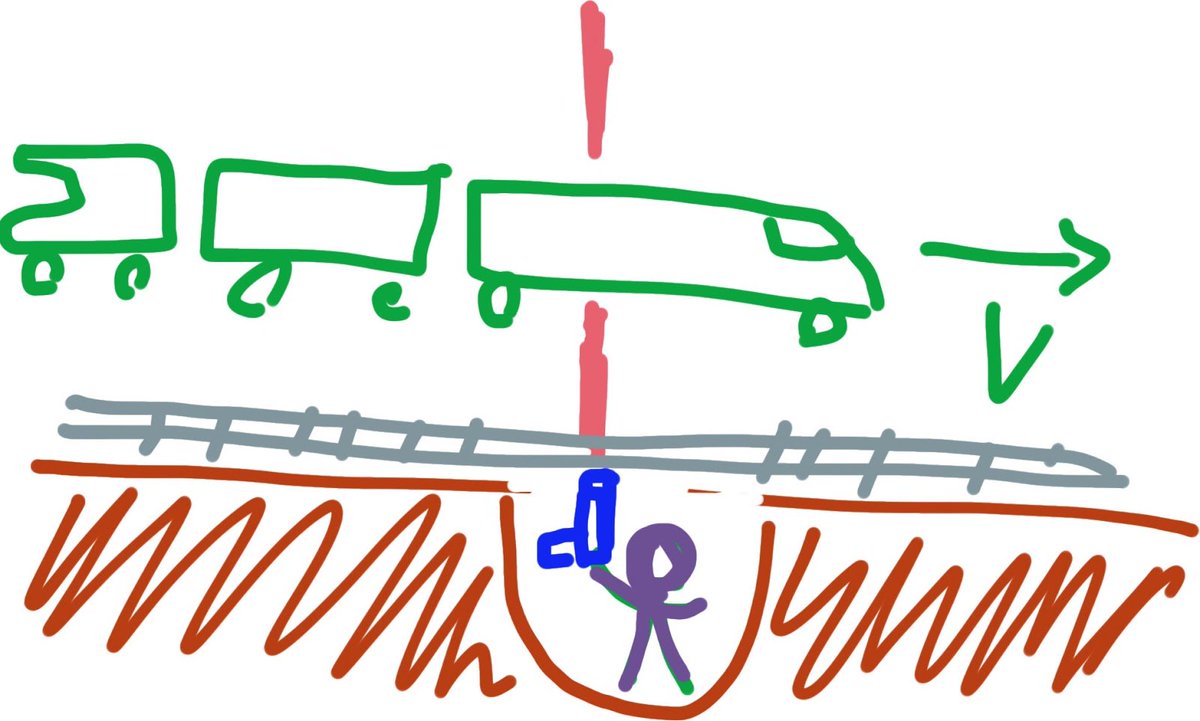 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
maxim-photo.sakura.ne.jp/contents/topo/… pic.twitter.com/WMddvbIBeP
2017-09-15 09:03:53 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
列車搭載の身長0メートル小人ガンダムの場合と、 砂漠線路レール下に埋めたガンダムの場合。 列車系から鉛直に光子ピストルを放った場合と、 線路系から鉛直に光子ピストルを放った場合、 列車床光子位置と列車天井光子位置がどうなるか。
2017-09-15 09:05:01 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
これを考える為に、まずは、列車が線路に対して動いているを どう定義確認するか、数学という頭の中の世界から飛び出て、 実験物理準備の世界に入りましょう。
2017-09-15 09:05:22 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
数直線をイメージし、 数直線は無限長さだから、 無限長さ全体そのものはイメージできず、 実数全体をRとかの記号で表すようなことをします。
2017-09-15 09:06:05 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
数直線の無限性長さから、有限区間を切り離すと、 部分空間として頭の中でもイメージできます。 黒板やノートに、適当な長さの線分区間を実験空間として描きます。
2017-09-15 09:06:24 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
数直線上で 博多駅を「-100位置」。 京都駅を「0位置。」 東京駅を「+100位置」。 実際の新幹線線路と違い、 博多駅より西にも線路は続き、 東京駅より東にも線路は続くとします。
2017-09-15 09:06:45 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
あなたが乗車している上り新幹線列車。 あなたが乗車している客車番号は「0号車」。 隣の東京に近い客車番号が「+1号車」。 隣の博多に近い客車番号が「-1号車」。 頭の中や黒板、ノートには有限でイメージしましたが、 線路は無限長さ。そして上り新幹線列車連結客車数も無限とします。
2017-09-15 09:07:09 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
いま、あなたは上り新幹線、 線分客車2光秒長さの中央に居る。 真下を見る。床は透明。 真下に枕木番号0の、枕木E位置を ゼロ距離観察した。
2017-09-15 09:07:51