
『アティヤの発表によると微細構造定数を導出したとのこと。リーマン予想はボーナス。個人的には微細構造定数の方が重要。本当ならば軽くノーベル賞クラス』
 Markus Pössel
@mpoessel
Markus Pössel
@mpoessel
Atiyah didn't set out to prove the Riemann Hypothesis. He was trying to derive the fine structure constant (yes, that thing from physics). The RH was just a bonus. #HLF18 pic.twitter.com/vaPpOgot19
2018-09-24 17:19:03 拡大
拡大
 x_seek
@x_seek0
x_seek
@x_seek0
アティヤの発表によると微細構造定数を導出したとのこと。リーマン予想はボーナス。個人的には微細構造定数の方が重要。本当ならば軽くノーベル賞クラス。 twitter.com/mpoessel/statu…
2018-09-24 18:45:32 math_jin
@math_jin
math_jin
@math_jin
これがAtiyahさんのリーマン予想証明の‥ pic.twitter.com/v1z2iXN67h
2018-09-24 14:21:41 拡大
拡大
 拡大
拡大
 拡大
拡大
 拡大
拡大
 math_jin
@math_jin
math_jin
@math_jin
アティヤさんのリーマン予想証明の講演が今流れてます! pscp.tv/w/1zqJVLeqXYDKB pic.twitter.com/NY2WST8KJE
2018-09-24 17:19:40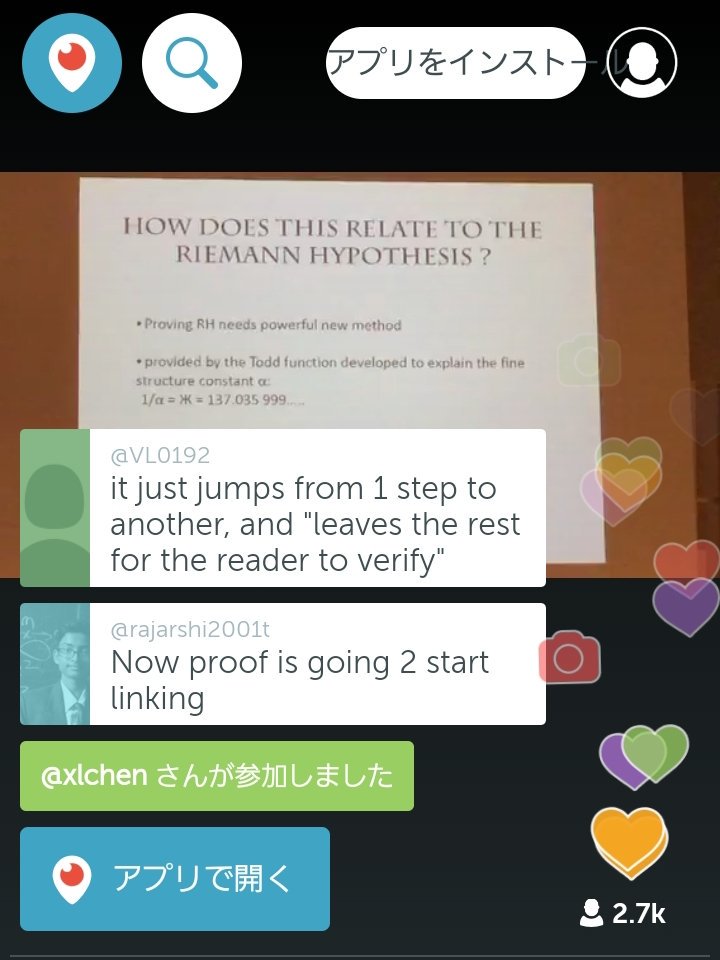 拡大
拡大
 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
アティヤ先生は、たった5ページのリーマン予想の証明の論文を既にpdfで公開してるようだ。 dropbox.com/s/pydoj0a8hgue…
2018-09-24 13:21:05 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
@putStr @matsumoring 引用されている[2]のアティヤ先生の論文が重要らしいのですが、それがないとなんとも。。
2018-09-24 13:48:56 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
これは「数学の専門家の意見乞う」パターン。なんか本当に証明になっているのかパッと見でわからない。(素人の個人的印象では、なんかとても怪しい。) #リーマン予想 #アティヤ先生 twitter.com/hottaqu/status…
2018-09-24 13:28:41 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
う~ん。自分も編集委員してる英国王立協会の雑誌にアティヤ先生が投稿したというこの論文にリーマン予想の証明の根幹が書いてあるそうだが、この論文が見つけられない。(編集委員でもこの論文は読めない)[2]M.F.Atiyah The Fine Structure Constant submitted to Proc.Roy. Soc A 2018
2018-09-24 13:41:53 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
そもそもこの[2]の論文自体もかなり大胆な内容が伺える。微細構造定数αについての物理学の論文らしいが、普通の感覚だと、かなり??な印象。晩年のディラックの大数仮説を彷彿とさせる感じだが、本当のところどうなのだろう。
2018-09-24 13:44:58 ザード@
@world_fantasia
ザード@
@world_fantasia
@hottaqu でも大数仮説って掛け算すると都合よくO(10^70)くらいのオーダーの数が現れるから、この大きさの定数が必要になる物理学理論を作れば、それが万物の理論になるはずだ(=あらゆる定数を統一する定数があるはずだ)って主張なのでそんなにぶっ飛んでないんですよね
2018-09-24 21:33:51 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
@world_fantasia ええ。でも今となっては。今回のアティヤ先生のもどうやらエディントンの焼き直しらしいです。
2018-09-25 05:19:45 Masahiro Hotta
@hottaqu
Masahiro Hotta
@hottaqu
アティア先生、物理学の微細構造定数αまで数学で求めた後に、リーマン予想まで解いたと話題になってるけど、少なくともαの証明は物理学者である個人として、評価できない。昔のエディントンの延長線の話に過ぎない。リーマン予想については、飽くまで専門の数学者の意見を乞うという状況。
2018-09-25 05:35:27『T(π)=1/α=137.035999... を満たすとされているのに、実際に数値計算してみると T(π)=1/α= 0.160259... となってしまうので、Atiyah卿の主張はおかしい、という声が上がっている』
 Yusuke Hayashi(林祐輔)
@hayashiyus
Yusuke Hayashi(林祐輔)
@hayashiyus
TL上で話題のリーマン予想について、Todd 関数は T(γ)/γ = T(π)/π かつ T(π)=1/α=137.035999... を満たすとされているのに、実際に数値計算してみると T(π)=1/α= 0.160259... となってしまうので、Atiyah卿の主張はおかしい、という声が上がっている。 twitter.com/duetosymmetry/…
2018-09-25 11:22:51 Leo C. Stein is @duetosymmetry@mastodon.social (⎷)
@duetosymmetry
Leo C. Stein is @duetosymmetry@mastodon.social (⎷)
@duetosymmetry
@johncarlosbaez Erm, combining Atiyah's Eqs. 1.1 and 7.1 in that PDF gives a number that is very, very different from the fine structure constant... or its reciprocal... pic.twitter.com/I1tUHWAI8Z
2018-09-25 01:18:28 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
Tomorrow Atiyah will talk about his claimed proof of the Riemann Hypothesis. It's all about "the music of the primes". Here the function that counts primes < n is being approximated by waves whose frequencies come from zeroes of the Riemann zeta function. (continued) pic.twitter.com/lzNDyXo3Im
2018-09-24 06:30:47 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
The Riemann zeta function is given by this simple formula when the complex number s has Re(s) > 1. Then the sum converges! But we can "analytically continue" the Riemann zeta function to define it for other values of s, and that's where the fun starts. (continued) pic.twitter.com/E6fUwdfNJF
2018-09-24 06:38:07 拡大
拡大
 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
The Riemann zeta function is zero for some numbers with 0 < Re(s) < 1. These are called the "nontrivial zeros" of his zeta function. Riemann computed a few and hypothesized they all have Re(s) = 1/2. youtube.com/watch?v=sD0Njb…
2018-09-24 06:49:59 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
Riemann found a formula for the number of primes < n as a sum over the nontrivial zeros of the zeta function. My first tweet shows the sum over the first k nontrivial zeros. So, if the Riemann Hypothesis is true, we'll get a better understanding of primes! (continued) pic.twitter.com/CbTvsCV1VE
2018-09-24 07:07:30 拡大
拡大
 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
I bet that Atiyah's claimed proof, if and when he writes it up, will not convince experts. In 2017 he claimed to have a 12-page proof of the Feit-Thompson theorem, which usually takes 255 pages: maths.ed.ac.uk/~v1ranick/atiy… He showed it to experts, and... silence. (continued)
2018-09-24 07:44:05 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
In 2016 Atiyah put a paper on the arXiv claiming to have solved a famous problem in differential geometry. The argument was full of big holes: mathoverflow.net/questions/2633… So, I'm not holding my breath this time. But of course I'd be happy to be wrong. (the end) pic.twitter.com/YPsR2FSd3M
2018-09-24 07:50:57 John Carlos Baez
@johncarlosbaez
John Carlos Baez
@johncarlosbaez
Here is Atiyah's lecture: on the Riemann Hypothesis youtube.com/watch?v=UBVy0o… Here, apparently, is his paper: dropbox.com/s/pydoj0a8hgue… It refers extensively to this much longer paper, where he attempts to compute the fine structure constant: drive.google.com/file/d/1WPsVht…
2018-09-25 00:58:34 Leo C. Stein 🦁
@duetosymmetry
Leo C. Stein 🦁
@duetosymmetry
@johncarlosbaez Erm, combining Atiyah's Eqs. 1.1 and 7.1 in that PDF gives a number that is very, very different from the fine structure constant... or its reciprocal... pic.twitter.com/I1tUHWAI8Z
2018-09-25 01:18:28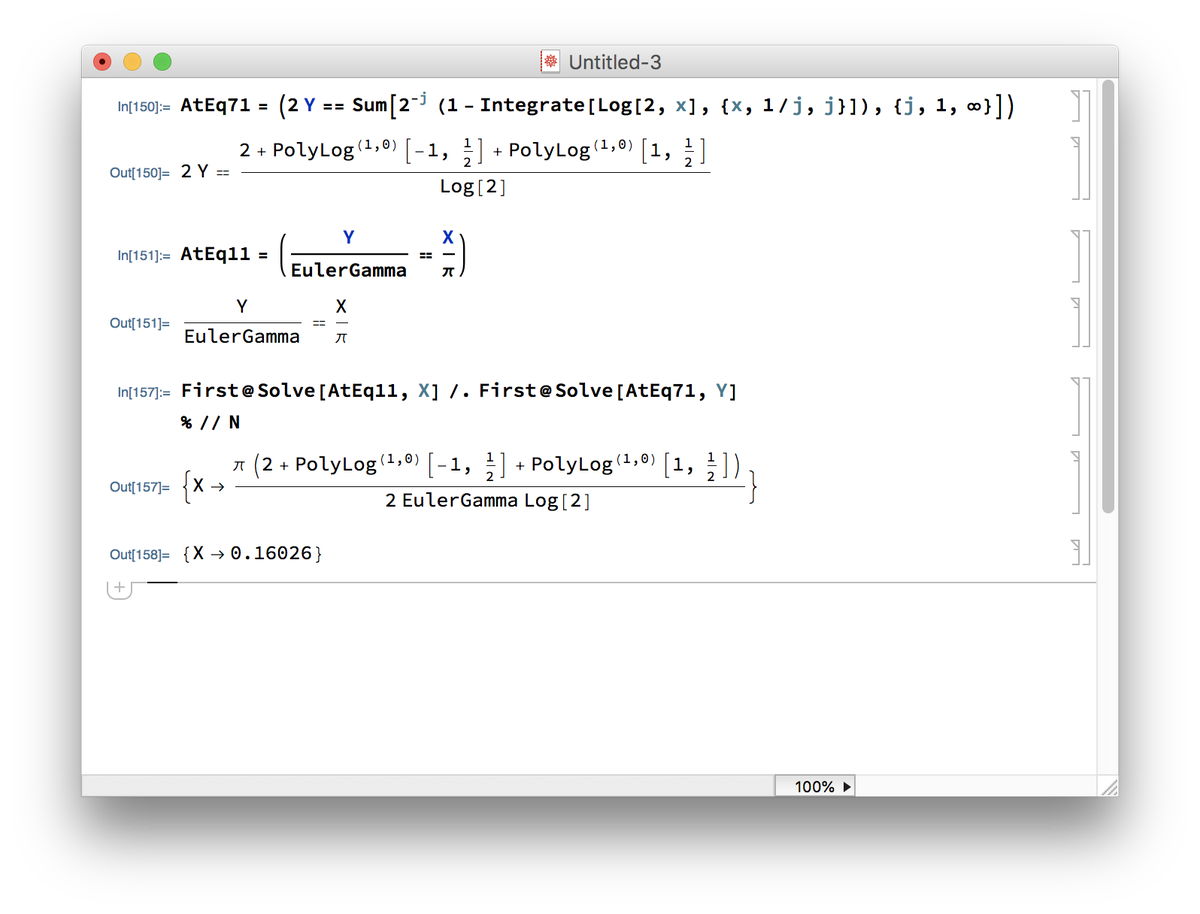 拡大
拡大
