@tsujimotter 【今日の数学豆知識】 をまとめてみた #数豆
-
tsujimotter
- 12776
- 0
- 0
- 0
-
- いいね！0
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【今日の数学豆知識】奇数の完全数はまだ見つかっていないよ。もちろん、存在しないことも証明されていません。※完全数とは…6や28のように、その数自身を除く約数がその数自信と等しい数のこと。
2013-07-17 19:43:08
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/18の数学豆知識】正十七角形はコンパスと定規で作図できるよ。作図可能であることを発見したのはかの有名なガウスです。 http://t.co/5mvRTdUMj6
2013-07-18 13:47:21
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/19の数学豆知識】719は、7つの連続した素数の和(89+97+101+103+107+109+113)で表されるよ。ほかにも、階乗素数（6!-1）だったり、ソフィー・ジェルマン素数などいろいろな特徴を持った面白い素数だよ。 http://t.co/0FqgoiMDjb
2013-07-19 20:04:03
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【補足】ちなみに719は陳素数とも呼ばれていて、陳素数は「p+2が「素数」か「素数2つの積」で表される素数p」のこと（719+2=7×103）。陳景潤は、未解決問題であるゴールドバッハ予想に迫るために、このタイプの素数が無限にあることを証明したんだって。
2013-07-19 20:14:13
tsujimotter ロマ数本好評発売中!!
@tsujimotter
続き）ゴールドバッハ予想が「p+2が素数であるような素数pは無限に存在するか？」という問題だから、すごく惜しい感じがするね。面白い！
2013-07-19 20:15:16
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/20の数学豆知識】正七角形は定規とコンパスを使って作図できない。けど、折り紙でなら作成可能だよ。折り紙すげえ！
2013-07-20 23:40:37
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/20の数学豆知識補足】折紙を使うと「角の三等分線」も引くことができるんだ。折紙と代数学の面白い関係についてはこの本を読んでみて♪ 折紙の数学 http://t.co/iYLpAh8w1N
2013-07-20 23:46:26
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/21の数学豆知識】1-(1/3)+(1/5)-(1/7)+...のように交互に奇数の逆数を足したり引いたりするとπ/4になるよ。整数を使った和が円周率になるのは面白いね。ただしこの和を計算しても、収束がものすごく遅くて役に立たないよ。詳しくは「ライプニッツの公式」でググって
2013-07-21 19:45:48
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/22の数学豆知識】本日は円周率近似値の日。22/7はπの近似値になっていて、約率という名前がついているよ。他の近似値に355/113(密率)があって、発見者は5世紀の数学者の祖沖之。円周率の連分数展開からも導出できるけど、当時彼がどうやって導いたかはよくわかっていないんだ。
2013-07-22 19:27:58
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/23の数学豆知識】係数が有理数の方程式の解とならない数のことを超越数と言います。πやeは超越数の代表的な例です。π+e^πやπe^πが超越数であることはすでに知られていますが、不思議なことにπ+eという簡単な和でさえ超越数かどうかわかっていません。
2013-07-23 21:56:07
tsujimotter ロマ数本好評発売中!!
@tsujimotter
もともとは、ギリシャ三大作図問題の「立方体と同じ体積の球は作図できるか」から来ている話だってのも面白い。
2013-07-23 22:04:22
tsujimotter ロマ数本好評発売中!!
@tsujimotter
てゆーか、e+πは無理数かどうかもよくわかってないんだよね。神秘的過ぎ。ちなみにGoogle電卓で計算すると、e+π=5.85987448205
2013-07-23 22:10:28
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/24の数学豆知識】ラマヌジャン数と呼ばれる e^(π√163) 、計算すると262537412640768744に限りなく近い値を取ります。 整数に限りなく近い値を取る非整数を「ほとんど整数」といいます。そんな適当な、と思うかもしれませんが、れっきとした数学用語です。
2013-07-24 16:02:32
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/25の数学豆知識】虚数単位 iのi乗は「複素数」ではなく「正の実数」になるんです。 http://t.co/jsVeqSWfC9
2013-07-25 18:24:51
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/26の数学豆知識訂正】ゲルフォントの定数（eのπ乗）は一般に証明が難しいと言われている超越数の代表例だよ。この数の超越性はゲルフォント＝シュナイダーの定理を使って証明できるんだ。ちなみにこの数からπを引いた数 e^π-π は20に限りなく近い「ほとんど整数」でもあるよ。
2013-07-26 22:22:01
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/27の数学豆知識】逆から読んでも元の数と同じような素数を「回文素数」っていうんだ。727は三桁の回文素数だよ。回文素数が無限にあるかどうかはまだわかっていないんだ。ちなみに偶数桁の回文素数は11しかないことが知られているよ。
2013-07-27 16:22:41
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/28の数学豆知識】100以下の素数の求め方。①2から100までの整数をすべて並べます。②2以外の2の倍数を除きます。③3以外の3の倍数を除きます。④同様に5, 7の倍数を除きます。⑤残った数がすべて素数です。 #エラトステネスのふるい
2013-07-28 17:11:43
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/29の数学豆知識】ある数Nが９の倍数であるか判定する方法。Nの各桁の数字の和を９で割り切れたら、N自身もは９の倍数。たとえば729は7+2+9=18が９で割り切れるため９の倍数。３の倍数も同じように判定できるよ。
2013-07-29 22:36:52
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/30の数学豆知識】「病的な関数」と呼ばれる関数があるよ。カール・ワイエルシュトラスというドイツの数学者によって提案された関数で、連続関数であるにもかかわらず至るところ微分不可能な関数だよ。見た目も確かに病的だね。 http://t.co/naAma6Rp2z
2013-07-30 22:40:41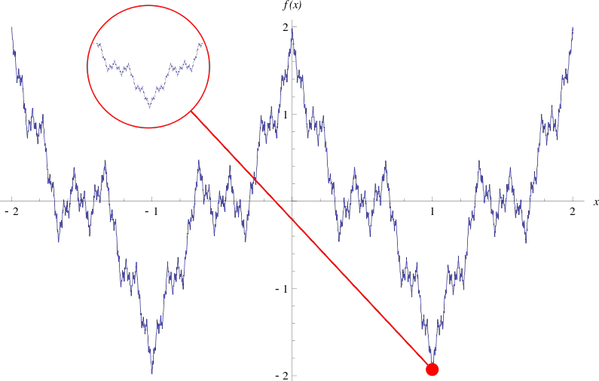
拡大
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【7/31の数学豆知識】「微細構造定数α」は量子電磁力学に出てくる有名な定数ですが、光速、電荷素量、プランク定数という重要な物理定数で表されます。1/αが面白いことに137に非常に近い値をとるんです。しかも、αは無次元量なので、どんな単位系でも同じ値になるのです。137は素数！
2013-07-31 22:27:17
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【8/1の数学豆知識修正】4で割って1余るすべての奇素数は、二つの平方数の和で表せるよ。逆に、二つの平方数の和で表せる奇素数は、4で割ると1余るよ。（例: 5=2^2+1^2、13=3^2+2^2、41=5^2+4^2）
2013-08-02 13:47:42
tsujimotter ロマ数本好評発売中!!
@tsujimotter
【8/2の数学豆知識】三角関数の引数でよく用いられるθは現代ギリシャ語にならって「シータ」と発音することが多いけど、古代ギリシャ語では「テータ」と発音していたそうだよ。楕円関数の一種のθ関数はテータ関数と呼ぶのが一般的だね。
2013-08-02 23:37:44