 mはげ
@Tw_Mhage
mはげ
@Tw_Mhage
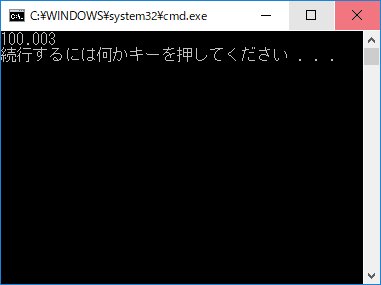
30年前の名著「数値計算の常識」を読んでたらBASICで0.01を10000回足したら100.003になるとか書いてあった。まあ昔のPCなんてそんなものかなと思いながら、Visual Studio 2017で試してみたら同じ結果だったw pic.twitter.com/HBwJhlhZjc
2018-11-17 23:20:07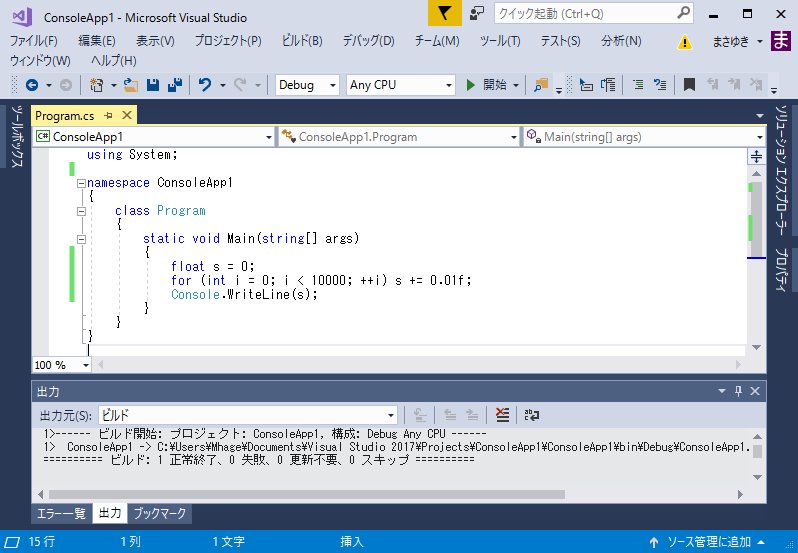 拡大
拡大
 拡大
拡大
 S (ツイートはスレッド全体をご確認ください)
@esumii
S (ツイートはスレッド全体をご確認ください)
@esumii
@Tw_Mhage @masanork ご参考まで、添付画像のような例もあります。JavaScriptではなくほとんどの言語でも同様です。浮動小数点演算はもう長らく変わっていないか、むしろGPU等では倍精度ではなく単精度に落ちているケースも多いと思います。唐突に失礼しました。 pic.twitter.com/JWHW1p616V
2018-11-17 23:37:36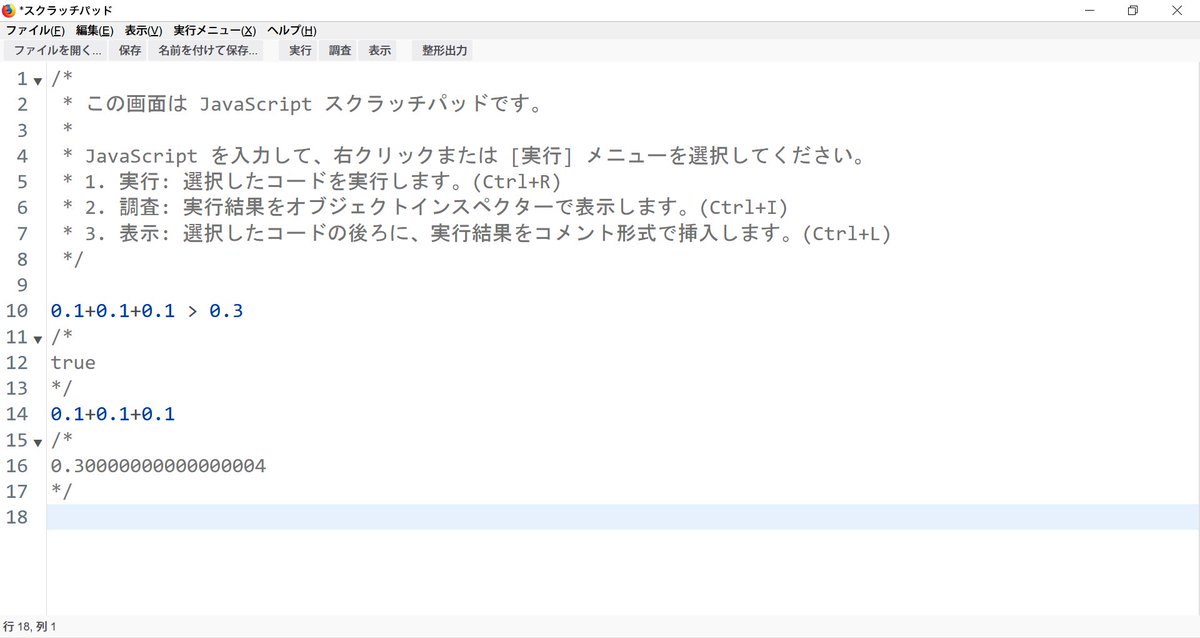 拡大
拡大
 mはげ
@Tw_Mhage
mはげ
@Tw_Mhage
@esumii @masanork ありがとうございます。コンピュータの処理速度は上がっても、上がってない性能もあるのですね。面白いですね。
2018-11-17 23:55:52 TokusiN
@toku51n
TokusiN
@toku51n
@Tw_Mhage @esumii @masanork 精度が必要なら100桁でも10000桁でも好きな精度で計算できますが、普通はそんなに必要ないので精度を上げていません。上がっていないのではなく、上げていないのです。
2018-11-18 01:15:39 雷更新世
@pleist
雷更新世
@pleist
@toku51n @Tw_Mhage 必要ないというより、いくら精度を上げても違う進数で微量のズレが出ることの解決にはならないですからね。
2018-11-18 01:32:49 TokusiN
@toku51n
TokusiN
@toku51n
@pleist @Tw_Mhage それを解決するために有理数型を使うこともあります。有理数の厳密な計算をしたいとき以外はまず使いませんが。
2018-11-18 01:34:18 雷更新世
@pleist
雷更新世
@pleist
@toku51n @Tw_Mhage そうなりますよね。そのへんの型を高速に扱える機構がCPUに組み込まれればまだしも。まあ需要がさほど無いでしょうし、結局いつまでも「小数は誤差を理解して使うのが常識」に落ち着くんでしょうね。
2018-11-18 01:42:18 こばさん
@wakwak_koba
こばさん
@wakwak_koba
@pleist @toku51n @Tw_Mhage 例示の通り C# を使うような用途だったらむしろ逆で、デフォルトを decimal 型としつつ、どうしても速度が必要、有効桁数がもっと必要、という場合だけ double 型を検討する、という風かなと思います。。
2018-11-18 10:19:46 耕士
@ysdkz
耕士
@ysdkz
@Tw_Mhage 浮動小数点表現のせいで不正確になるなら、常に多めか常に少なめかのどちらかになる気がするのですが、気持ち悪いことに足す回数で、多めになったり、少なめになったりします。画像は500回足した結果で、正確な値より少なめです。表示の際に下の桁を四捨五入とかしてるんでしょうか? pic.twitter.com/zFIKRjd2iP
2018-11-18 23:38:32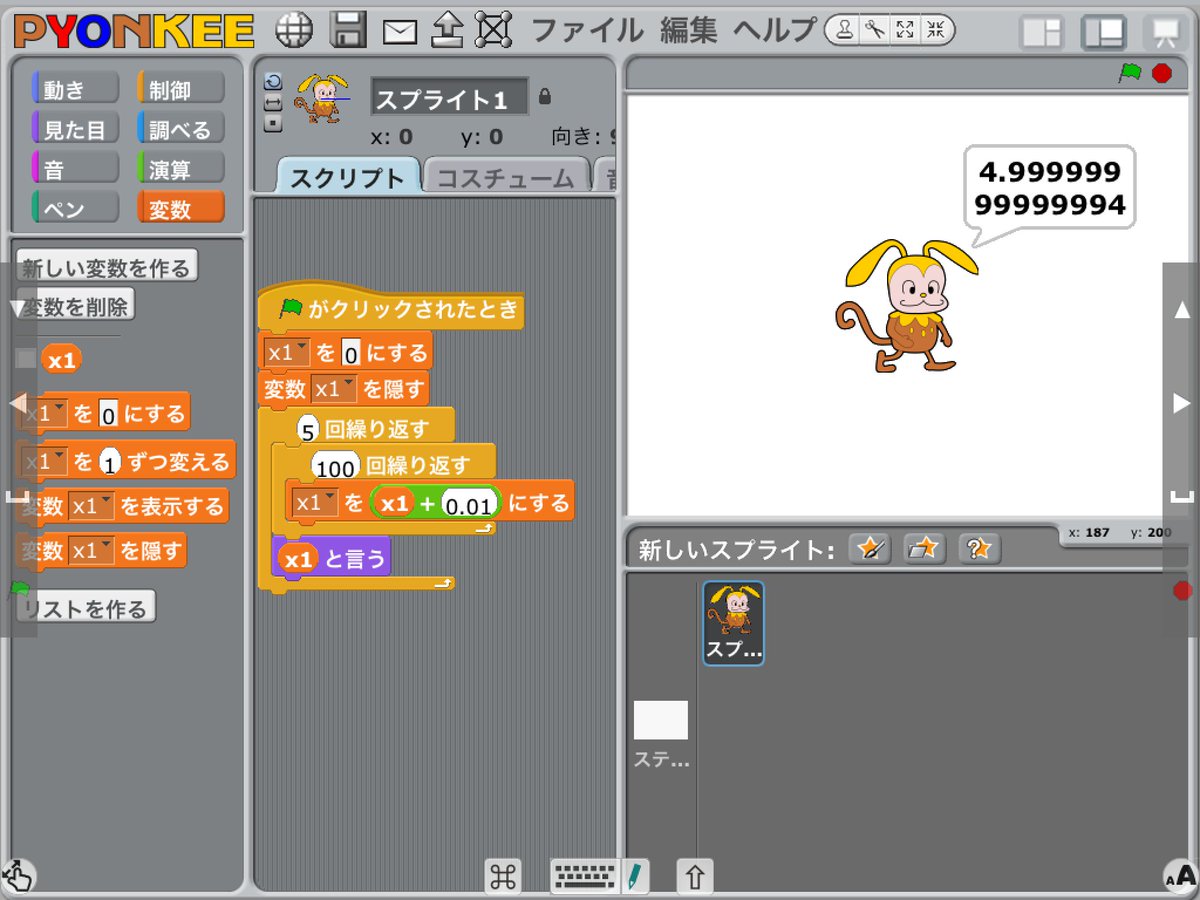 拡大
拡大
 mはげ
@Tw_Mhage
mはげ
@Tw_Mhage
@ysdkz 誤差の原因は2つです。実は2つ目の方が支配的です。 また2つめは多め少な目どちらも起こりえます。 1. 10進数を2進数の32bit浮動小数点に変換した際の丸め誤差(表現誤差) 2. 大きい数(今までの合計)と小さい数(これから足す数)の足し算時の桁落ち誤差
2018-11-19 00:13:32 tarosuke
@tarosukenet
tarosuke
@tarosukenet
@Tw_Mhage 十進で言えば例えば1/3 * 3000とかを限られた桁数でやるようなもん。例えば三桁なら1/3は0.333で、これに3000かけても999になる。1000にはならない。 一般化するとn進で1/mを表現するときにはmの素因数が全てnの素因数に含まれてないと有限桁では正しく表現できない。二進じゃ素因数は2しかない(ry
2018-11-18 02:06:43 海王星スープ (Neptune soup)
@miiisuEX
海王星スープ (Neptune soup)
@miiisuEX
@Tw_Mhage @karaage0703 この本もってる・・・。ダンボールの中にあるはず。 あの、ご迷惑でなければ何ページに載っているか教えていただけますでしょうか。
2018-11-17 23:36:37 海王星スープ (Neptune soup)
@miiisuEX
海王星スープ (Neptune soup)
@miiisuEX
@Tw_Mhage @karaage0703 返信&回答ありがとうございます。 参考になります。
2018-11-18 00:08:56 梨
@picocastle
梨
@picocastle
@Tw_Mhage @hmatsumu 興味が湧いて64bitコードにしてdoubleでもやってみましたが、やはりしっかり計算出来ないんですね。 勉強になりました。 pic.twitter.com/9lf96S2Cu5
2018-11-18 13:04:15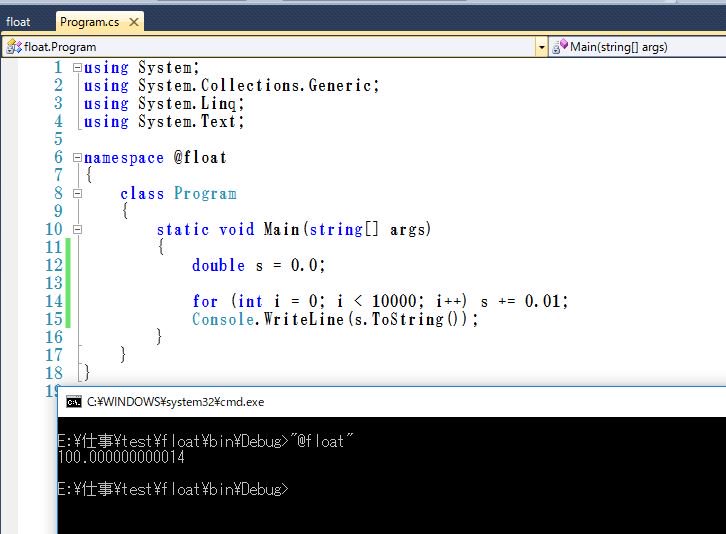 拡大
拡大
 lunablanca
@lun_blanc
lunablanca
@lun_blanc
@picocastle @Tw_Mhage @hmatsumu 横からすみませんが明朝体でコーディングしてるの初めて見ました…!
2018-11-18 16:39:46