-
groebner_basis
- 8511
- 28
- 0
- 0
-
- いいね！0
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム①】 まずは、次の問題を考えるぶなっ！ 問題「辞書式順序 x>y において、二変数多項式 x^2*y+x*y^2+y^2 を xy-1 で割り算せよ。」 紙とペンを用意して、実際に筆算してみるぶなっ！！ pic.twitter.com/TeVDjPWCwK
2015-10-02 22:14:04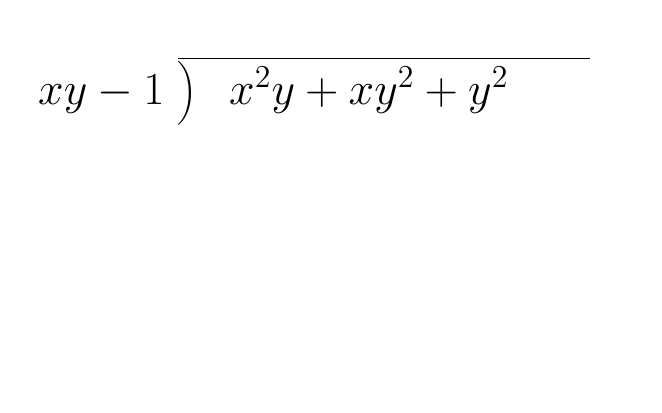
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム②】 まず、f=x^2*y+x*y^2+y^2 の辞書式順序x>yにおける先頭項はLT(f)=x^2*y でg=xy-1 の先頭項はLT(g)=xy ぶなから、f から g×x を引くぶなっ！ pic.twitter.com/VAcAX9jwr9
2015-10-02 22:18:15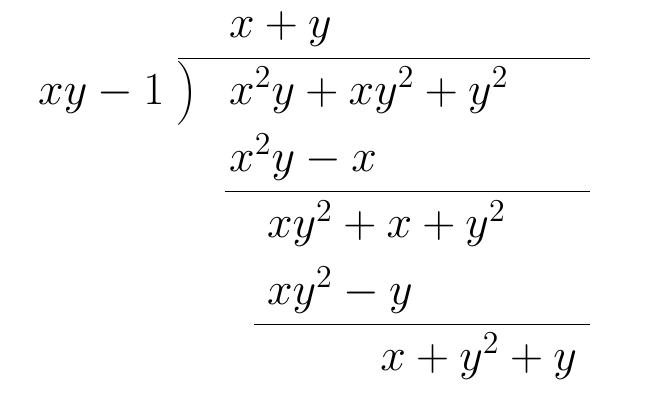
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム③】 すると、x*y^2+x+y^2 が出てきて（これも辞書式順序で並べていることに注意！）、この先頭項はx*y^2ぶなから、これからg×yを引くぶなっ！そして、x+y^2+y が出てくるぶなっ！ pic.twitter.com/z7cU15QM2r
2015-10-02 22:22:07
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム④】 このx+y^2+yの先頭項はxで、これはLT(g)=xy で割れず、また他のy^2,yも同じく割れないので、ここで割り算が終了するぶな！よって、商としてx+y、余りとして、x+y^2+yが答えとして出たぶな！ pic.twitter.com/WWeBGTgxIU
2015-10-02 22:24:58
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑤】 今度は、さっきの多項式 x^2*y+x*y^2+y^2 を二つの多項式 xy-1 と y^2-1 で割ることを考えるぶなっ！ pic.twitter.com/Klj6OYGb3z
2015-10-02 22:29:56
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑥】 xy-1 が最初に来ているので、途中までさっきと同じように計算するぶなっ！すると、x+y^2+y が出てくるぶなね。この先頭項xは、LT(y^2-1)=y^2でも割れないぶな。よって、xを取り除いて考えるぶな pic.twitter.com/Z4nteU4AJM
2015-10-02 22:36:27
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑦】 すると、y^2+y となって、今度の先頭項はLT(y^2-1)で割れるぶな。よって、(y^2+y)-1*(y^2-1) を計算すると、y+1になるぶな！ pic.twitter.com/xAX2qtAU8A
2015-10-02 22:40:20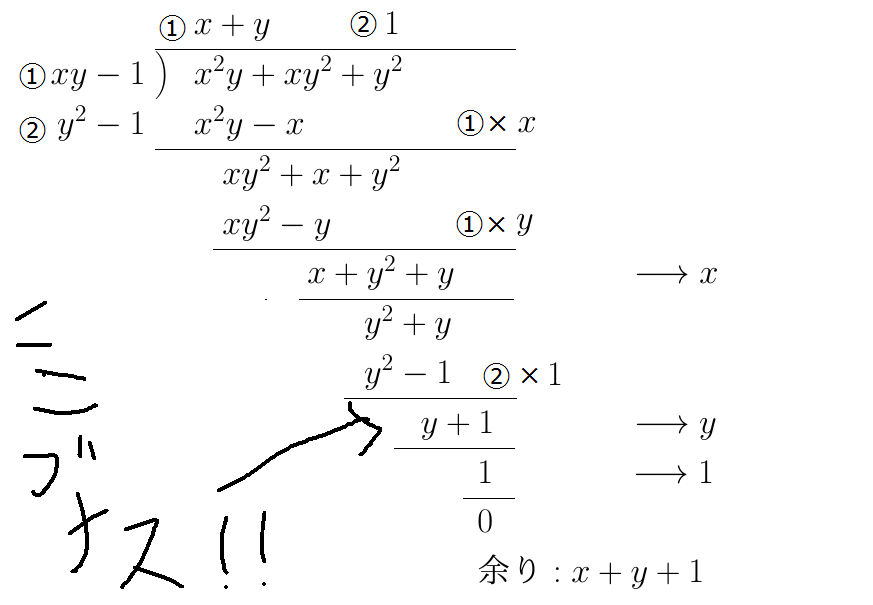
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑧】 y+1 の先頭項yはLT(xy-1)でもLT(y^2-1)でも割れないので、y+1からyを取り除くぶな！同様に1も取り除いて、最後に0になったので割り算終了ぶなっ！ここで取り除いたものの和を余りとしてみるぶな pic.twitter.com/9ZLS2UwzGZ
2015-10-02 22:45:52
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑨】 ここでそれぞれの商として、x+y、1、余りとして、x+y+1 が出てきてるぶな。 つまり、 x^2*y+x*y^2+y^2=(x+y)*(xy-1)+1*(y^2-1)+x+y+1 が成立しているぶな！ pic.twitter.com/tFlJfqyzTd
2015-10-02 22:52:24
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑩】 上の式を、f=a*g+b*h+r をとして見ると、 ①multideg(f)≧multideg(a*g) , multideg(b*h) ② r に含まれるどの単項式もLT(g),LT(h)で割り切れない ことぶなっ！ただし、≧は辞書式順序。
2015-10-02 22:58:08
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑪】 実際、確認してみるぶな。multideg(f)とはfの先頭項の次数だったぶなから、この場合(2,1)ぶな。そしてa*gとb*hの次数はそれぞれ、(2,1)と(0,2)だから確かに (2,1)≧(2,1) かつ (2,1)≧(0,2) が成り立っているぶな
2015-10-02 23:02:11
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑫】 ②に関しても、r=x+y+1 のどの単項式x,y,1もLT(g)=x*yでもLT(h)=y^2 でも割れないので、成り立っているぶなね。実は、これが「割り算アルゴリズム」と呼ばれるものの重要な性質ぶなっ！ま
2015-10-02 23:05:04
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑬】 【定理】 単項式順序≧を一つ固定する。 多項式f_1,…,f_sとfに対し、あるa_iとrが存在し、 f=a_1*f_1+…+a_s*f_s+r で ①deg(f)≧deg(a_i*f_i) ②r=0か、rに含まれるどの単項式もLT(f_i)で割れない。
2015-10-02 23:12:16
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑭】 （字数の関係上省略したぶなけど）i は１からｓまでの整数で、①、②の中では１からｓまで動き、またdegはmultidegを意味しているぶな。上の定理を証明するのが、さっきやった「割り算アルゴリズム」ぶな。
2015-10-02 23:16:17
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑮】 正確な証明では、図のようなアルゴリズムを考えるのぶなけど、おそらく慣れてない人には少し難しいので、「さっきの例でやったようにやればいいんだなあ」と思ってくれていいぶなっ！ pic.twitter.com/j4rXUw1YrC
2015-10-02 23:19:11
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑯】 ここで大事なのは、【グレブナー基底の定義】でもやったように、「割り算アルゴリズム」での余りは、「割る順番」によって変わる可能性があるぶなっ！つまり、「余りが一意的ではない」ぶなね。では最初の例で、「順番を変えて」割り算をしてみるぶな。
2015-10-02 23:21:58
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑰】 すると、 f=(x+1)*h+x*g+2x+1 となり、今度は商として、x+1とx, 余りとして2x+1が出てきたぶなっ！この時も、性質①、②を満たしているぶな。最初の場合と比べてみると面白いぶなね。 pic.twitter.com/lhsLgQfzGh
2015-10-02 23:27:14
拡大
拡大
グレブナー基底大好きbot
@groebner_basis
【割り算アルゴリズム⑱】 これで、一番最初のぶなつい「グレブナー基底の定義」に出てきた「多変数多項式の割り算」がちゃんと定義できて、グレブナー基底が厳密に定義できたぶなあああああ！！！！やったぶなああああ！！来週は、グレブナー基底の同値な「扱いやすい」定義を導入していくぶなよっ！
2015-10-02 23:30:52
グレブナー基底大好きbot
@groebner_basis
今日の参考文献も togetter.com/li/877168 [1] ぶなよっ！第２章に載っているぶなしー！
2015-10-02 23:38:27