-
 zionadchat
zionadchat
- 2046
- 0
- 0
- 0
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
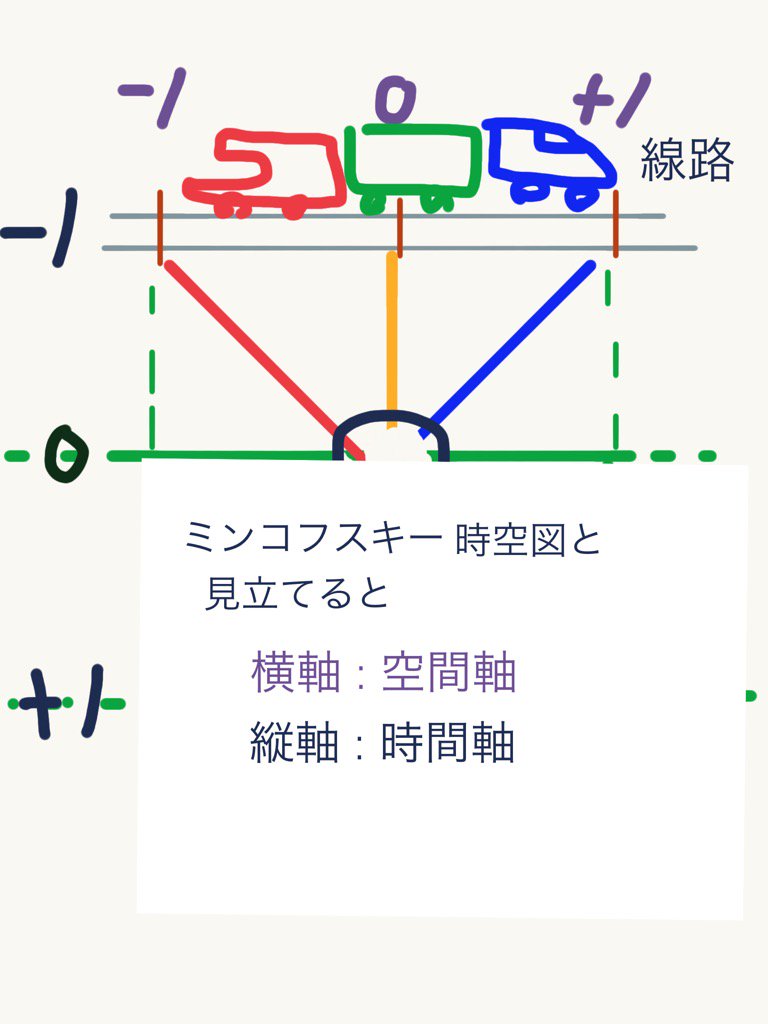
長さ2の正方形。上辺が注目してる線路区間2光秒長さ。 下半分は、ピンホールカメラ。 pic.twitter.com/lFP2K2rAem
2017-04-08 07:29:47 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ピンホールカメラは、レンズ口径が点の大きさ。ピンホールが焦点となって、スクリーンに像を上下左右逆さまに映す。 線路線分区間2を直径2の円錐底面と見立てた場合。 いまは円錐底面の直径だけで考える断面図的なもの。 pic.twitter.com/yN12ekbf9o
2017-04-08 07:54:55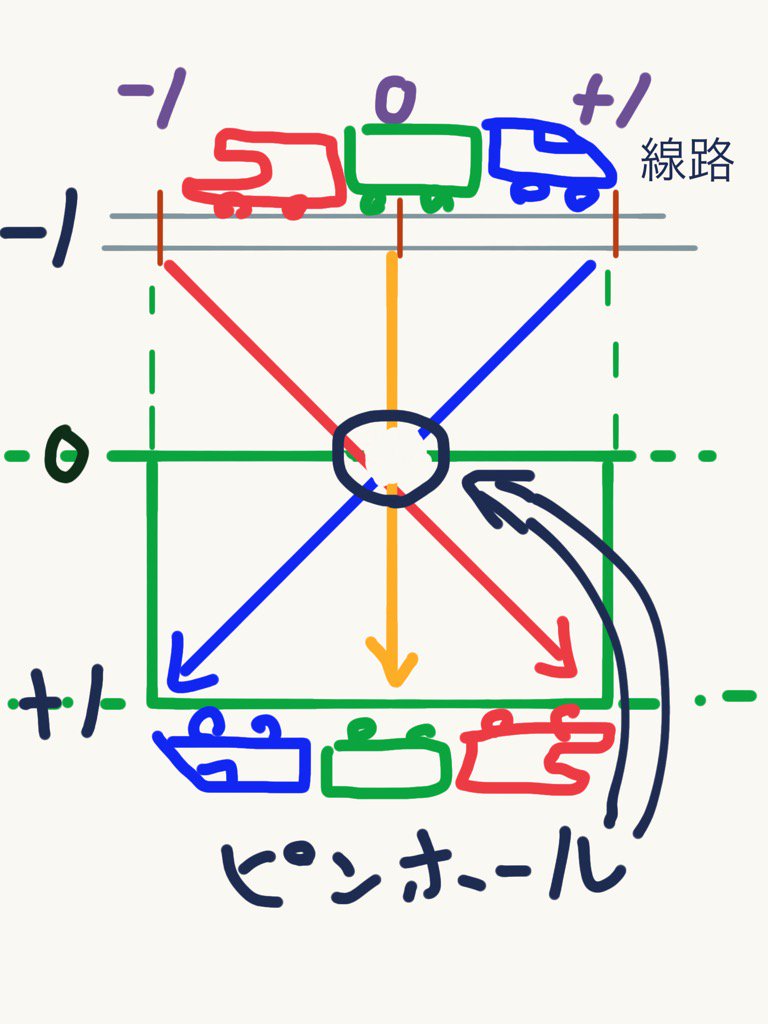 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
西洋と異なり、チャイナともかな。日本列島地域では、鉋(かんな)や鋸(のこぎり)、包丁は引いて使う。 だから過去光円錐に相当する方を平面絵図下にではなく、窓外を見る感じで奥行き方向に過去を置き、 それを平面に無理やり描いているので、撮影者より平面上、被写体が上になってる。 pic.twitter.com/9pJZnNXIbh
2017-04-08 12:49:50 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
「地獄が下・天国が上」の感覚で、「過去を下・未来を上」にする時間軸じゃなく、 撮影者と被写体を横軸に描く。 直線型加速器を平面横軸に描き、平面を忍者屋敷の回転扉のように縦軸Y軸で回転させると、直線型加速器の一端が被写体。画面からはみ出て、インドの方の額の赤点が撮影者位置。 pic.twitter.com/Pu4Z49ntVN
2017-04-08 13:03:47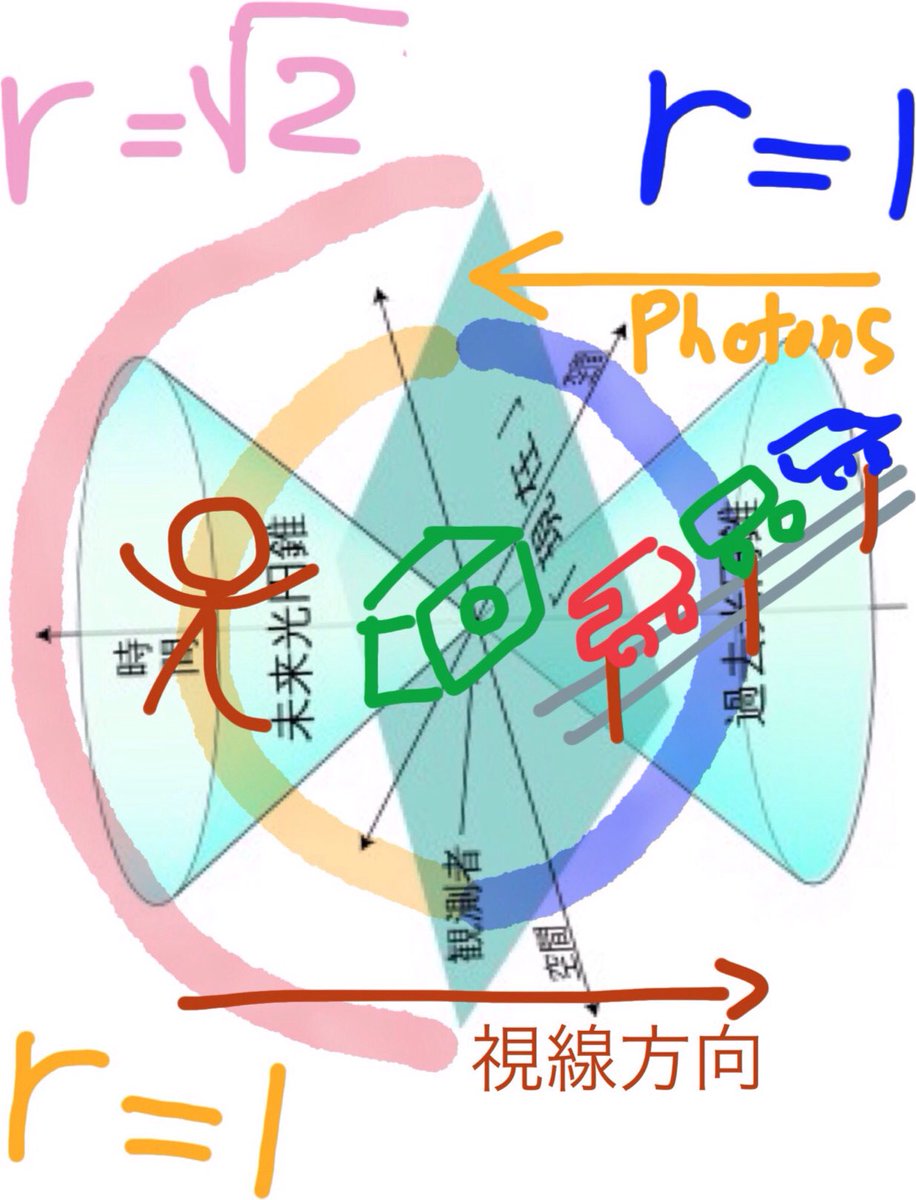 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
r=1というのは、線分2長さを直径とする円錐底面半径。 r=√2というのは、長さ2の正方形に外接する円錐底面半径。 ミンコフスキー時空図だと、過去光円錐底面円周の情報が、現在時の局所点に位置するピンホールに、斜め45度角で座標移動する情報伝達光子が辿り着くかどうかの過去光円錐。
2017-04-08 13:22:47 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
過去円錐底面、線分型は列車速度1秒間軌跡対応。0≦Vx1秒≦Cx1秒。 過去円錐底面、対角線型は、従来説、列車に搭載された光時計筒内光子が1秒間に描く軌跡長さ。 0≦斜線長さ≦√2。 つまり、アインシュタイン氏を天才と崇拝する視野狭窄理論物理学者ミチオカクは、不可能を見てる。 pic.twitter.com/XigUH1Mp82
2017-04-08 14:03:33 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
1秒間に、ピタゴラスの斜辺である、1より長い光子斜線軌跡を現在時の局所点観察者が見たとするのは不可能。 1秒間に光子軌跡は、どんな慣性系からでも、1長さにしか記述できないと定義したのがアインシュタイン氏の世界観なのだから。
2017-04-08 14:06:26 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
斜線は厳密にはピタゴラスの定理。長さの二乗と長さの二乗だけど、光速C二乗と列車速度V二乗と書いてる。 光時計筒姿は、1秒後のもの。 光時計筒天井に光子が到着した映像は、√(c^2+V^2)になる。 これが頓知問題に引っかかった理由。奥行き方向に過去度合いえがくべきだった。 pic.twitter.com/qsqrAjrqrk
2017-04-08 14:29:22 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
この図は、現在時点(ミンコフスキー図の)を、光時計筒の任意の1点の動きを時刻マイナス1秒から時刻0にミンコフスキー時空図に描いたもの。 列車のどこか1点に注目し、その観察者は到着点に居る感じ。 同様に光時計筒内光子が天井に到達した位置から、光子の床出発を描いてる。 pic.twitter.com/8oFQmwgTFn
2017-04-08 15:44:40 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
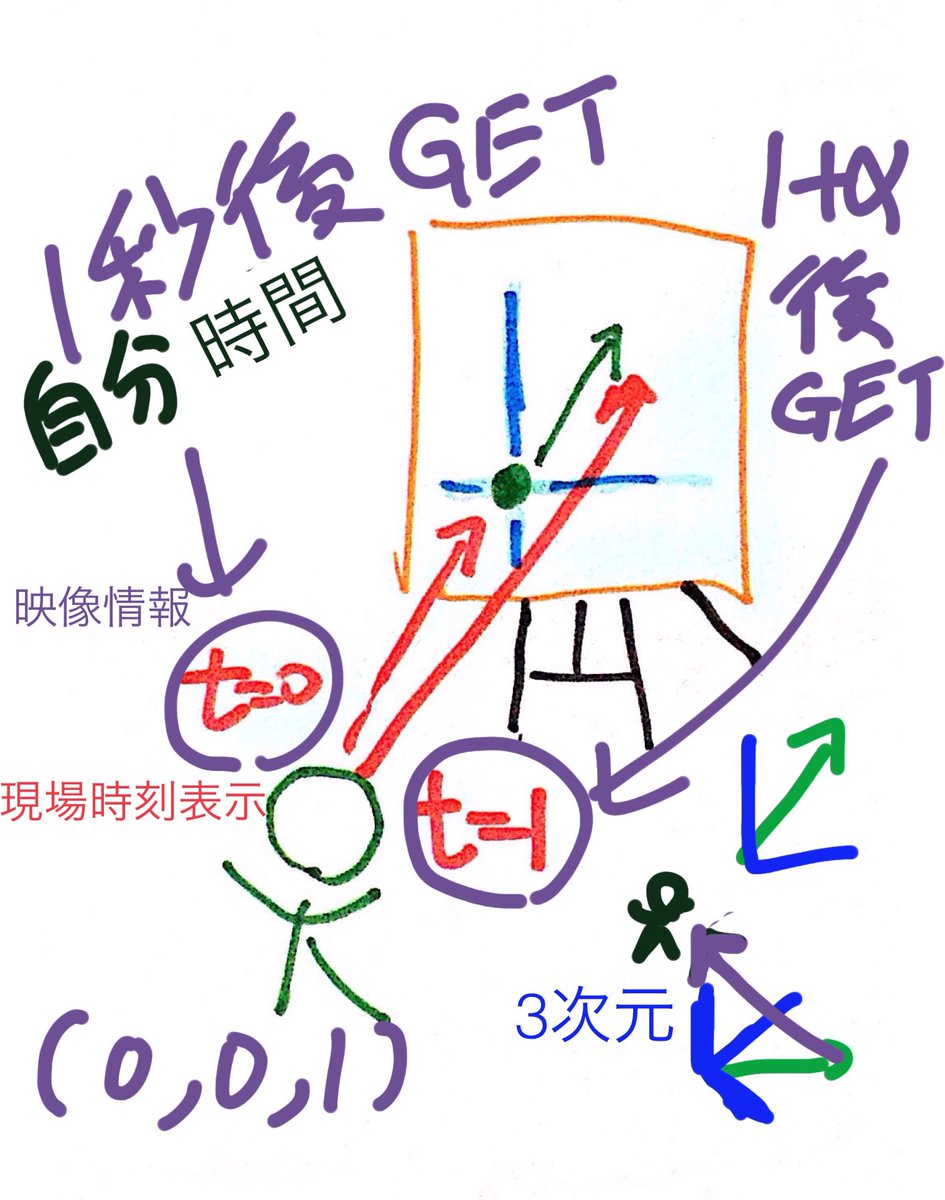
だが、アインシュタイン氏の提唱・提言は生きている。 平面を見下ろす3次元空間内の高見、局所点から、マイケルソン&モーリーの実験を見ればいい。 宇宙人の宇宙船を具体的に描き、地球を下に見る、或いは、窓外奥行きに地球が横ズレする視線距離導入すれば、アインシュタイン氏、やはり天才。 pic.twitter.com/76HfHJfH3F
2017-04-08 14:48:15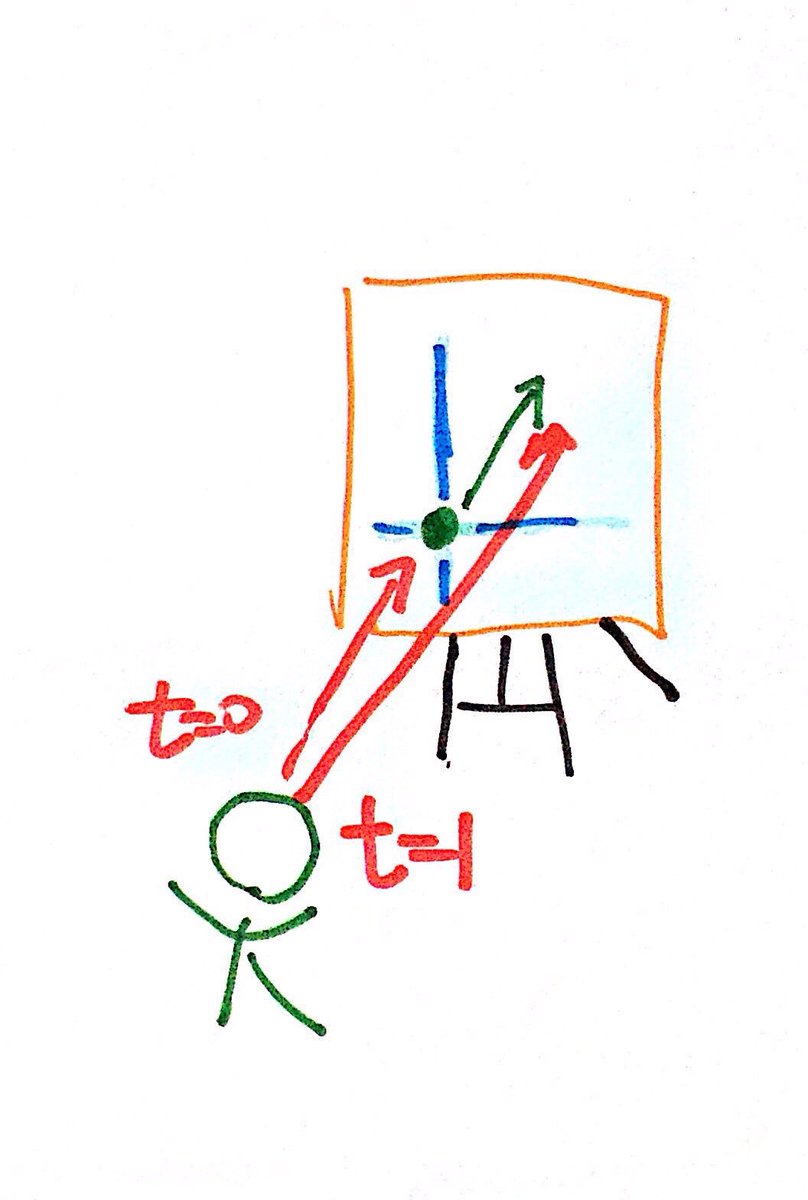 拡大
拡大
 拡大
拡大
 拡大
拡大
 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
撮影者と被写体の位置関係は水平で表し、 列車の進行方向は、斜めで立方体や建物を平面に描く感じで。 仕方ないので、撮影者と被写体が同時に年老いていく様を、下から上への経過時間。ノーマルなミンコフスキー時空図と同じ感じに描いた。 真ん中は、ピンホールカメラ。 pic.twitter.com/h8n5jMM66h
2017-04-08 13:17:53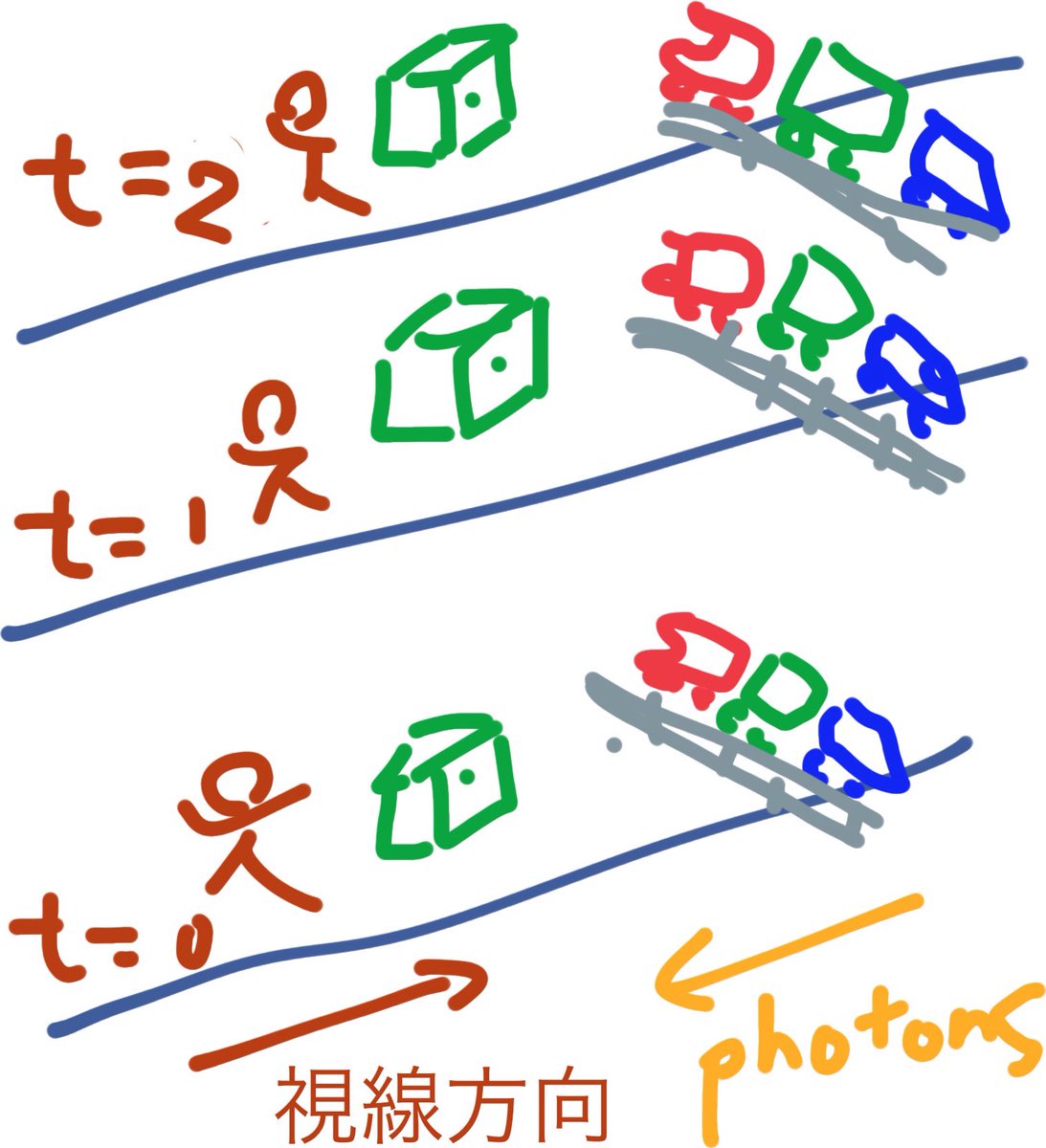 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ピンホールカメラと被写体である列車の離れは、空間的なもの。 ミンコフスキー時空図では、時間軸だからピンホール現在時点と過去事象発生被写体は、時間的離れ。 pic.twitter.com/itLpIAT3QS
2017-04-08 15:06:03 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
だから、ピンホールカメラの点孔(てんあな)と被写体列車とが、下敷きと下敷きをゼロ距離でこすり合わせてる感じ。 あとで、この奥行き空間。長さを撮影するには視野角が要るの話はする。 今回は飛ばして、 pic.twitter.com/GoM0crBHNz
2017-04-08 15:11:17 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
カメラで視野角が同じなら、奥行きをとらないと列車や線路の長さが写真フレーム枠に入らないように、 ミンコフスキー時空図では、過去に遡(さかのぼ)らないと長さを記述できない。 1次元の左右なら、1秒記憶収集すれば、2光秒長さ記述できる。 pic.twitter.com/3BchqV4SPH
2017-04-08 16:11:45 拡大
拡大
 zionadchat39
@zionadchat39
zionadchat39
@zionadchat39
ミンコフスキー時空図を同心円で描き直したら、列車各部の同時刻映像情報が見れるようになっちゃった。 さあ、あとは奥行き空間、被写体との、扱うピンホールカメラとの整合性を用意すれば、ローレンツ収縮は物理的になくて、ローレンツ変換が、整合性を保つ同時性の換算表になる話へ、GO! pic.twitter.com/XJDJ0FfbqI
2017-04-08 16:25:42 拡大
拡大
 zionadchat
@zionadchat
zionadchat
@zionadchat
trickzionad.blogspot.jp/2016/04/mokuji… pic.twitter.com/UR0B2LtM60
2016-09-27 04:52:27 拡大
拡大
 zionadchat
@zionadchat
zionadchat
@zionadchat
物理カテゴリ 断片営業 寓話「裸の王様」 特殊相対性理論を「検証」する。 1.慣性系毎の時の流れは本当なのか? 2.同時性が破綻しているとされてきたが、本当か? 3.ローレンツ収縮とローレンツ膨張。100年の見直しへ! trickzionad.blogspot.jp/2017/02/blog-p…
2017-03-23 18:09:11