おはろんり💕(パート３❣)⊕⊕ 論理回路学⚡演習問題と解答 ⊕⊕ カルノー図 ⊕ 論理関数の簡単化 ⊕１変数～４変数 ⊕ ドントケア項や乗法形も，任せてﾈ⭐
-
kairogakutan
- 8974
- 48
- 0
- 0
-
- いいね！0
「論理回路学」入門用の，くわしい問題と解答・解説。パート３です。
パート２は，下記から読めるョ❢
(パート２❣)⊕⊕【論理回路学】⚡問題と解答 ⊕⊕ ブール代数の計算 ⊕ 論理関数の加法形＆乗法形・標準形 ⊕「加法..
パート１に続き，演習問題と解答・ていねいな解説で，デジタル論理回路学に入門できちゃいますっ⭐
試験前のお勉強や実力チェック，復習などに使ってﾈ💡
範囲は ⚡ブール代数 / ⚡ド・モルガンの法則 / ⚡同等な論理式 / ⚡双対な論理式 / ⚡拡張ド・モルガンの法則 / ⚡排他的論理和の計算 / ⚡加法形，(主)加法標準形 / ⚡乗法形，(主)乗法標準形 / ⚡加法標準形と乗法標準形の双対性 / ⚡標準形の価値や意義や使い方・求め方・計算ﾃｸ。
次パートは，「カルノー図」のﾏﾄﾒに続くﾖ❣
6594 pv
85
パート１も：
⊕⊕回路学たん💡にｵｿﾜる【論理回路学】問題と解答（パート１）⊕⊕⚡ ２進数と論理演算の基礎 ⊕ 補数 ⊕ 回路素子..
演習問題と解答・ていねいな解説で，論理回路学に入門できちゃいますっ⭐
試験前のお勉強や実力チェック，復習などに使ってﾈ💡
範囲は ⚡二進法 / ⚡負数と補数 / ⚡小数表現とシフト演算 / ⚡論理演算と回路素子 / ⚡全加算器と半加算器。
次パートは，「ブール代数と標準形」のﾏﾄﾒに続くﾖ❣
14667 pv
82
2 users
⭐前回のあらすじ⭐
前回のパート２では，
論理回路を論理式で表現するための方法として
・ブール代数
・ド・モルガンの法則
・加法形と(主)加法標準形
・乗法形と(主)乗法標準形
などを学びました。
今回はパート３㌨ 💡
てーまは
「カルノー図による，論理関数の簡単化」
だｮっ♡
論理回路学たん (情報工学の学術たん)
@kairogakutan
ここまでで， 論理回路学・演習問題と解答の 「ブール代数と標準形」 の範囲はｵｼﾏｲです☆ 要点 ・ブール代数の計算。 ・加法標準形の求め方。 ・乗法標準形の求め方。 ・加法標準形と乗法標準形が双対である事の，証明の仕方。 この４つが自信もってできていれば， この範囲は合格っ！
2019-07-15 14:32:32
論理回路学たん (情報工学の学術たん)
@kairogakutan
ここからは ＜論理回路学の演習：カルノー図編＞ だよｯ☆ミ ・真理値表とカルノー図の違いは，何ｶﾅ❓ ・ブール代数だけでなく，カルノー図が必要なのはなぜｶﾅ❓ ・加法形や加法標準形と，どう関係するｶﾅ❓ ・３～４変数で，ドントケア項を考慮し カルノー図を使いこなせるｶﾅ❓
2019-07-16 18:32:31ちなみに，論理回路の要点のまとめチャート：
論理回路学たん (情報工学の学術たん)
@kairogakutan
各項目に (1)～(9)までの番号を付して 再度，投稿し直し pic.twitter.com/ZpXOK8f4Hl
2019-07-18 12:05:06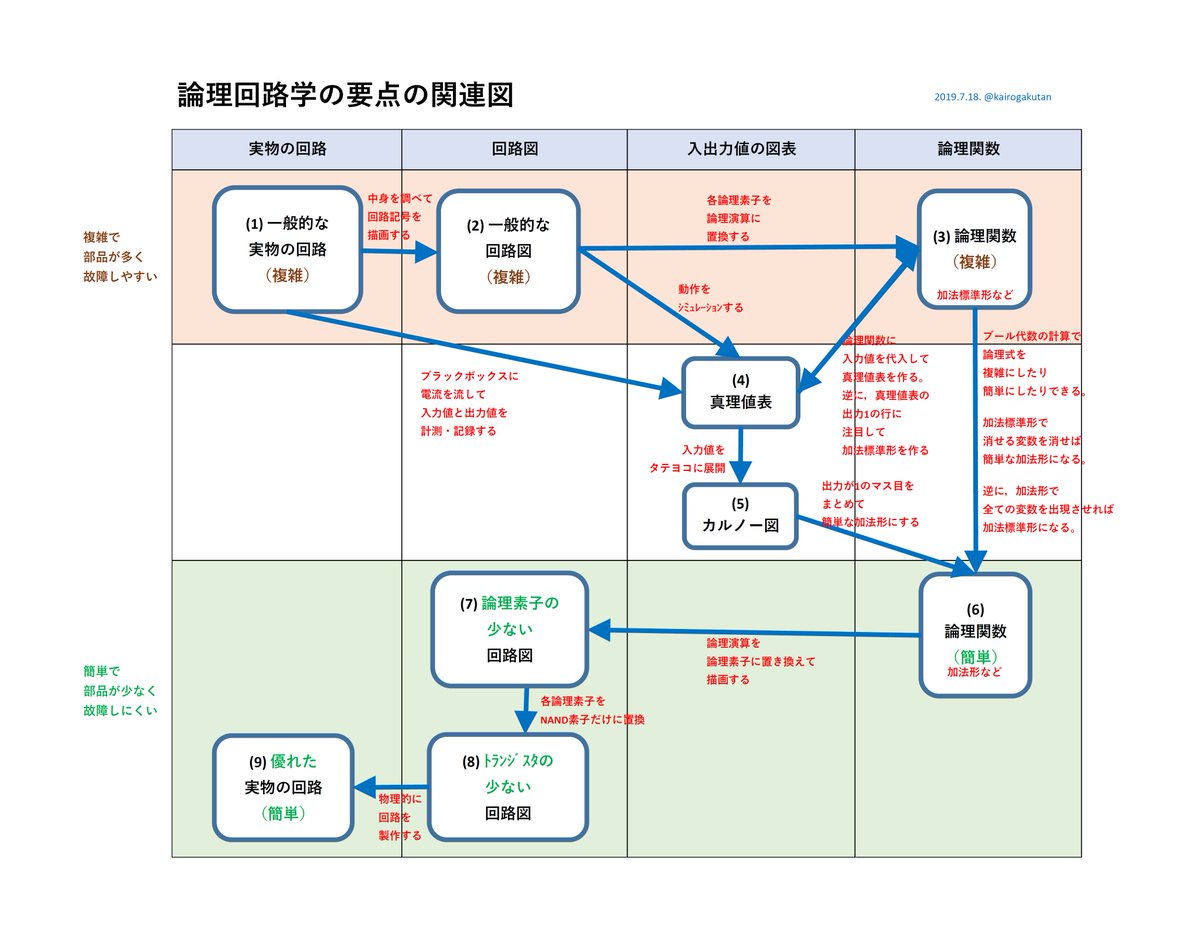
拡大
（セクション１８） カルノー図の目的。「簡単」とは何か？
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q. 真理値表とカルノー図の違いは，何ｶﾅ❓ A. 真理値表は， 入出力のセットをヨコ１行にまとめて， その行をタテ１列に並べる。 出力は0と1を書く。 カルノー図は，入力セットをタテとヨコに分解して， 出力のマス目を平面上に広げる。 出力は主に，1のみをマス目上に書く。
2019-07-16 19:06:33
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q あえて 真理値表ではなく カルノー図を使う 理由や目的は何ｶﾅ❓ A 論理関数の表記を簡単化することができるから。 カルノー図では 「出力が1の隣り合ったマス目どうし」をまとめて 論理関数を簡単化できる。 （真理値表は，１列に並んでいるだけなので 出力をまとめることができない）
2019-07-16 19:32:31
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q カルノー図の目的は， 論理関数の表記を簡単化する事でした。 では，そもそも 論理関数の表記を簡単化する事の目的は 何ｶﾅ❓ A 論理関数の表記が，簡単になれば 論理回路の構成がシンプルになる。 つまり， 回路の部品を減らすことができる。
2019-07-16 20:06:33
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q カルノー図の目的は 論理関数の表記を簡単化する事で， 論理関数の表記を簡単化する事の目的は 論理回路の部品を減らすことでした。 では，そもそも 論理回路の部品を減らすことの目的は 何ｶﾅ❓ A 回路の部品が少なければ， 回路の作成や修正のコストが減り， 故障率も下がるから。
2019-07-16 20:32:32
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q カルノー図の目的は 「論理関数の表記を簡単化する」事ですが， 「論理関数の表記を簡単化する」ためには カルノー図以外に どんな別の手法があるｶﾅ❓ A ブール代数の計算で 論理関数を簡単化することができる。（すでに学んだ） 例えば AB＋A￢B＝A(B＋￢B)＝A・1＝A
2019-07-16 21:06:32
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q 論理関数を簡単化する というのはつまり， 具体的に何がどうなれば， その論理関数が簡単化されたことになりますか❓ A 加法形で表した時に，OR接続された項の数が少なくなること。 そうすれば，簡単化されたと言える。
2019-07-16 21:32:32
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q Z1＝AB＋A￢B Z2＝A それぞれ，OR接続された項の数はいくつｶﾅ❓ 論理回路として，優れているのはどちらｶﾅ❓ A. Z1は２項 Z2は１項 回路として優れているのは Z2。 Z2のほうが 部品が少ないから回路を作成しやすく，動作も把握しやすく 故障も少ない。 なおZ1を簡単化するとZ2になる。
2019-07-16 22:06:32（セクション１９） １変数のカルノー図
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q 入力Xについて 「１変数のカルノー図」 のテンプレートを書いてﾈ A 下図の通り。 １変数の場合，カルノー図は 真理値表と変わりません pic.twitter.com/9aKpLKe5RY
2019-07-16 22:32:31
拡大
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q １変数Xを入力に取る論理関数 Z＝￢X カルノー図を書いてﾈ A 下図の通り。 入力Xに対して， 出力Zが１となる場合だけ 出力のマス目に「１」と書く （出力「０」は，書いても見づらくなるだけなので，書かない） pic.twitter.com/QD8Q65B7gV
2019-07-16 23:06:33
拡大
（セクション２０） ２変数のカルノー図
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q 入力X，Yについて 「２変数のカルノー図」の テンプレートを書いてﾈ A 下図の通り。 真理値表だと 起こり得る入力の全パターンの組み合わせを書くのが めんどいよﾈ❓ X Y 0 0 0 1 1 0 1 1 でもカルノー図は 全「入力の組み合わせ」を マス目で楽に表現できるんです pic.twitter.com/lOGhSTAZTc
2019-07-16 23:32:32
拡大
論理回路学たん (情報工学の学術たん)
@kairogakutan
Q ２変数X，Yを入力に取る論理関数 Z＝￢X＋￢Y カルノー図を書いてﾈ A 下図の通り。 これを書くためには まず先に真理値表を書く。 X Y Z 0 0 1 0 1 1 1 0 1 1 1 0 この真理値表を見ながら，またはイメージしながら， カルノー図のマス目を埋めればよし。 pic.twitter.com/knYddSLojq
2019-07-17 00:06:32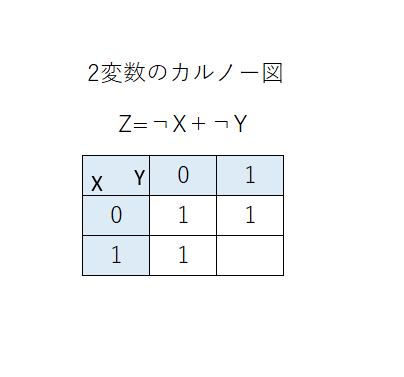
拡大