-
TokioHelvetica
- 69642
- 178
- 180
- 313
-
- いいね！313
NHK デザインあneo
@nhk_ah_neo
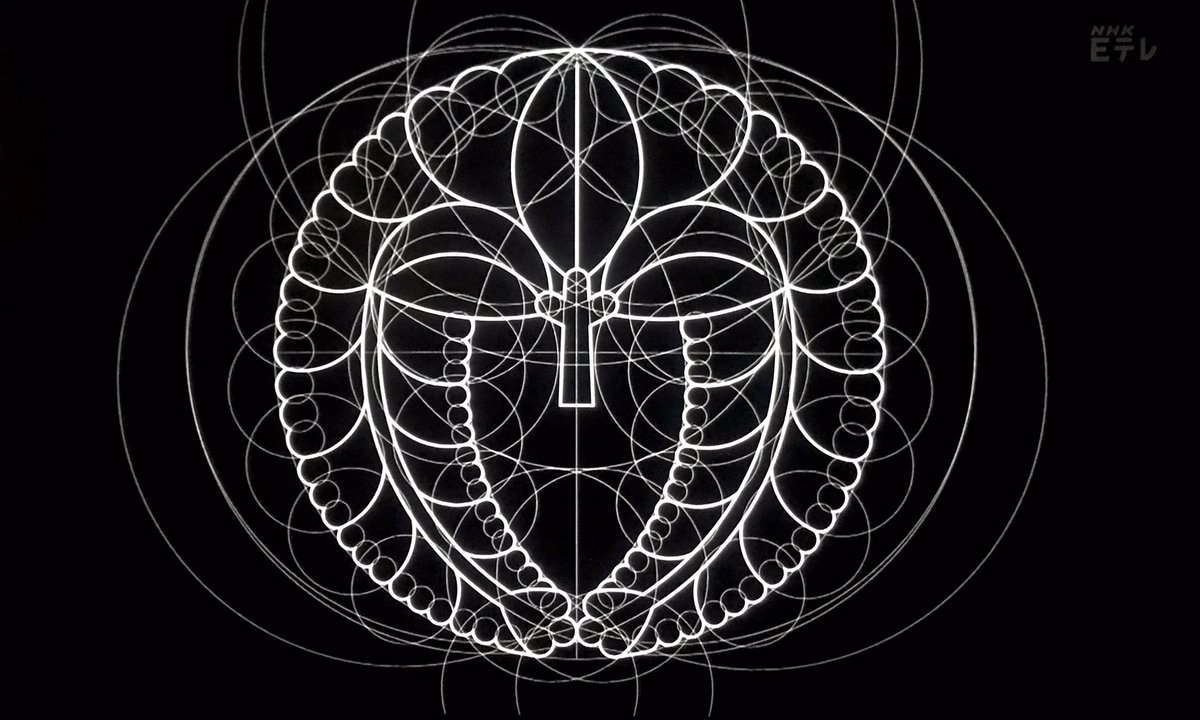
デザインあ おとなスペシャル2020 日本の伝統的なもんは、コンパスと定規だけで描いていることを、ご存じですか？ おとなSPでは、職人さんに伝わる作図法を、現代の数学でひもといてみます。語りはもちろん、渡辺篤史さん。解説は、数学講師のヨビノリたくみさんです！ 1月2日(木) 夜10:15 Eテレ pic.twitter.com/aKgrVgF7vj
2019-12-29 17:00:57
rieco
@rieco_maracas
コンパスと定規だけで複雑な家紋を家紋を描く職人の技を数学で解説。 家紋職人の基本、五角形描き方 #デザインあ pic.twitter.com/XKb8JmQ6aV
2020-01-03 09:52:55
拡大
拡大
拡大
転生準備中
@Elizabeth_H_01
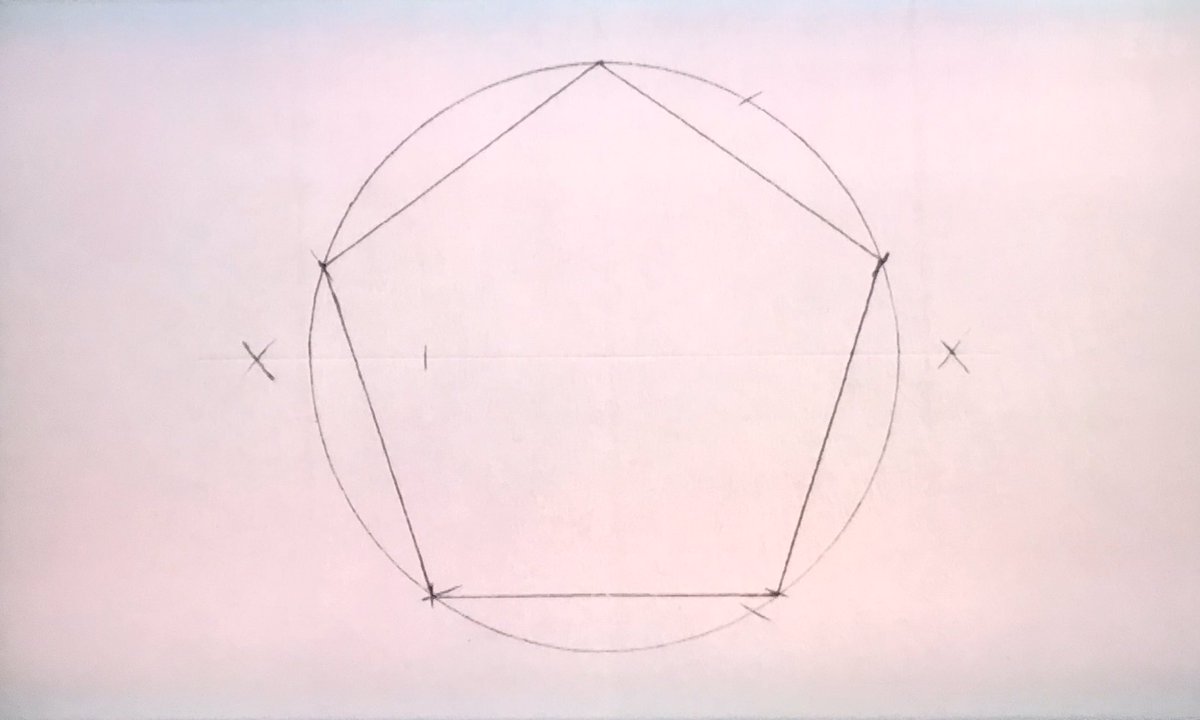
基本中の基本といいつつ定規とコンパスで正五角形の作図という高度な技術をやるスタイル #デザインあ #デザインあおとなスペシャル
2020-01-02 22:24:04
rieco
@rieco_maracas
半径の真ん中を求め、頂点と結びます #デザインあ pic.twitter.com/wh5whZXRdW
2020-01-03 09:53:51
拡大
拡大
拡大
拡大
rieco
@rieco_maracas
半径の真ん中と頂点を結んだ線を半径とする円を描いた反対側の半径と交わった点と頂点を結んだ線が、五角形の一辺の長さとなります #デザインあ pic.twitter.com/9xRIueGKrl
2020-01-03 09:53:58
拡大
拡大
拡大
ライアンヌ
@fibber
作図すごい。 数学ってデザインにも重要なんだけど、授業中は気づかない不思議。 そういえば、昔のデザイン系のソフトってこんな感じで五角形とか星とか書いてたよね。 #デザインあ
2020-01-02 22:26:26
rieco
@rieco_maracas
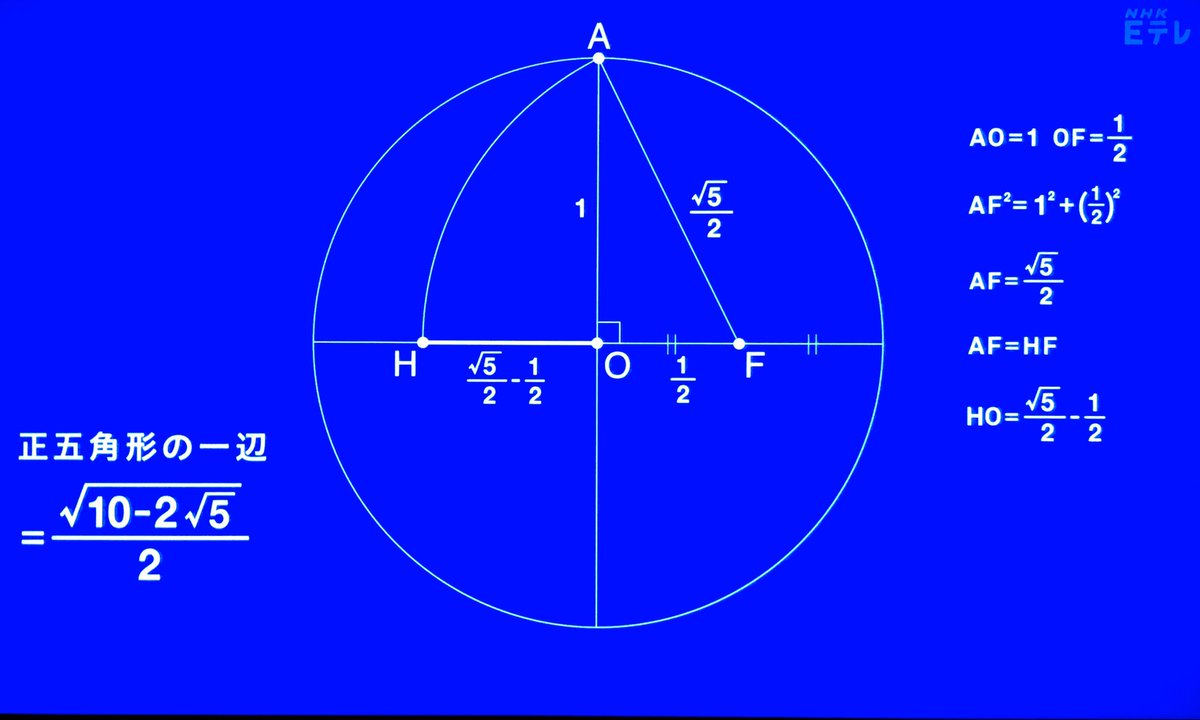
職人の技を数式であらわすとこうです #デザインあ pic.twitter.com/mPX5HW8jXy
2020-01-03 09:54:06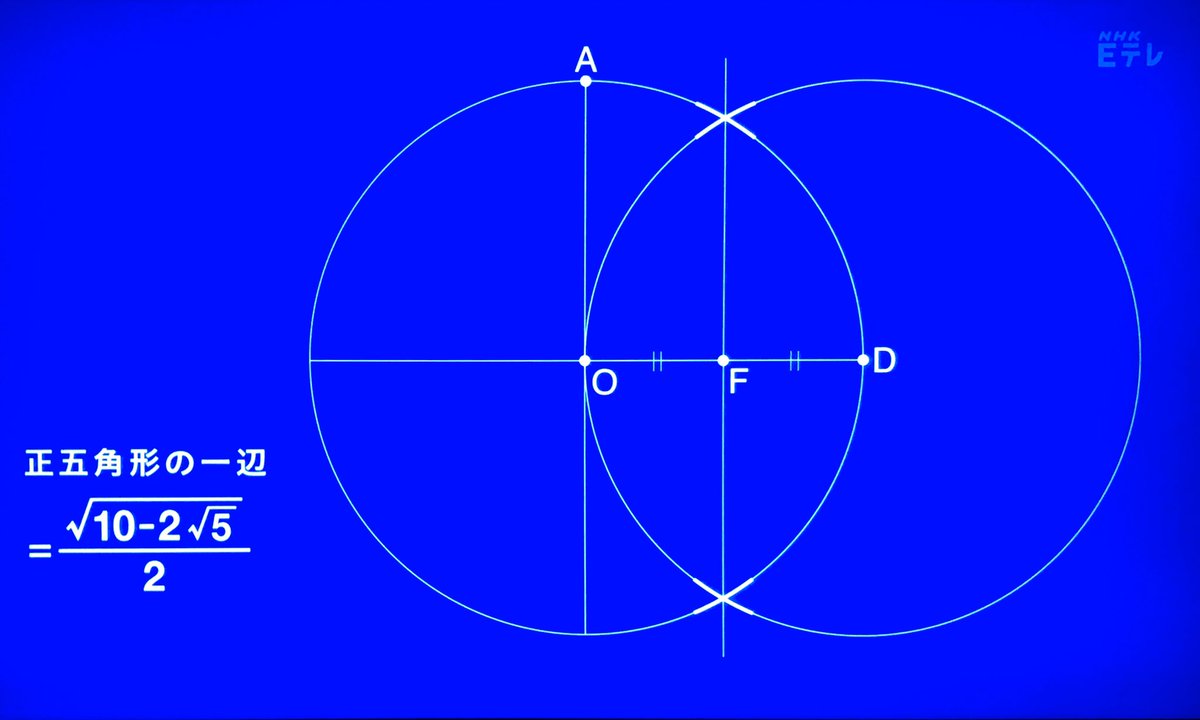
拡大
拡大
拡大
拡大
rieco
@rieco_maracas
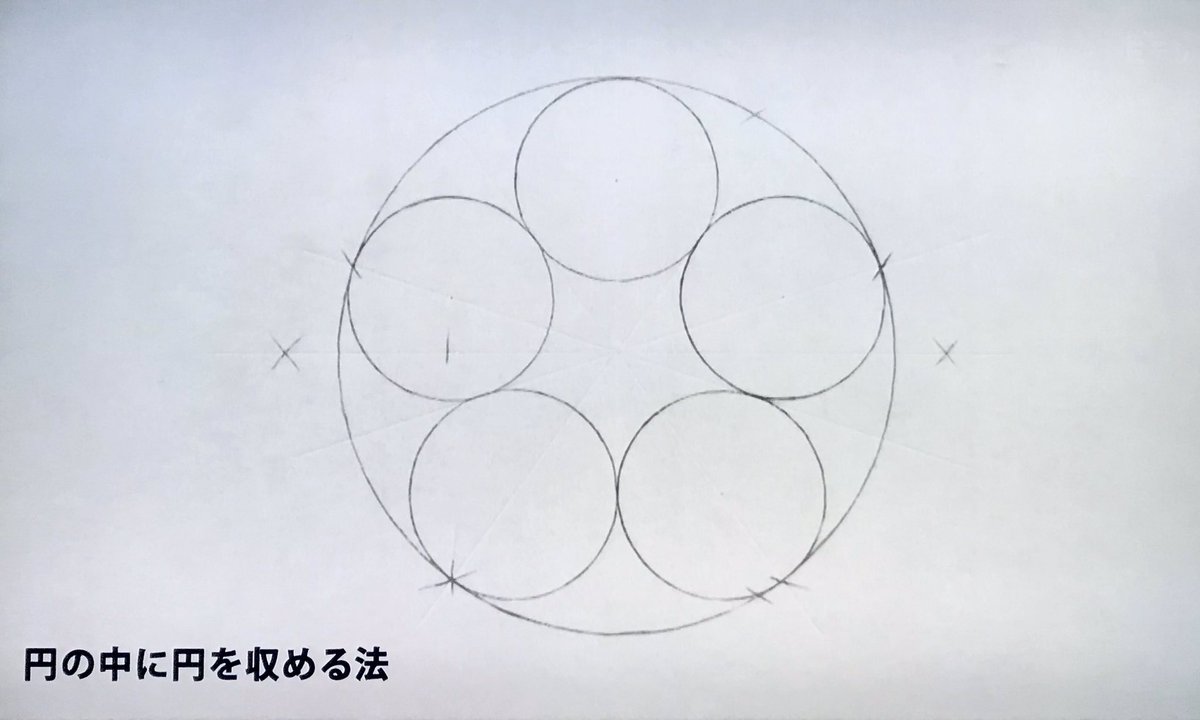
五角形を使って円の中にぴったり収まる５つの円を描きます #デザインあ pic.twitter.com/uAspMR3sz8
2020-01-03 09:54:13
拡大
拡大
まちゃおじ
@macha_oji
円の中に５つの円を きれいに収める数学 デザインあ おとなスペシャル２０２０ #design_ah #デザインあ #etv #Eテレ
2020-01-02 22:26:59
rieco
@rieco_maracas
五角形を10等分します。 半径を高さとする二等辺三角形の頂点から辺状に等距離な2点を打ち、その点を中心とした同じ大きさの円を描きます #デザインあ pic.twitter.com/WMpoim0tMo
2020-01-03 09:54:19
拡大
拡大
拡大
拡大
rieco
@rieco_maracas
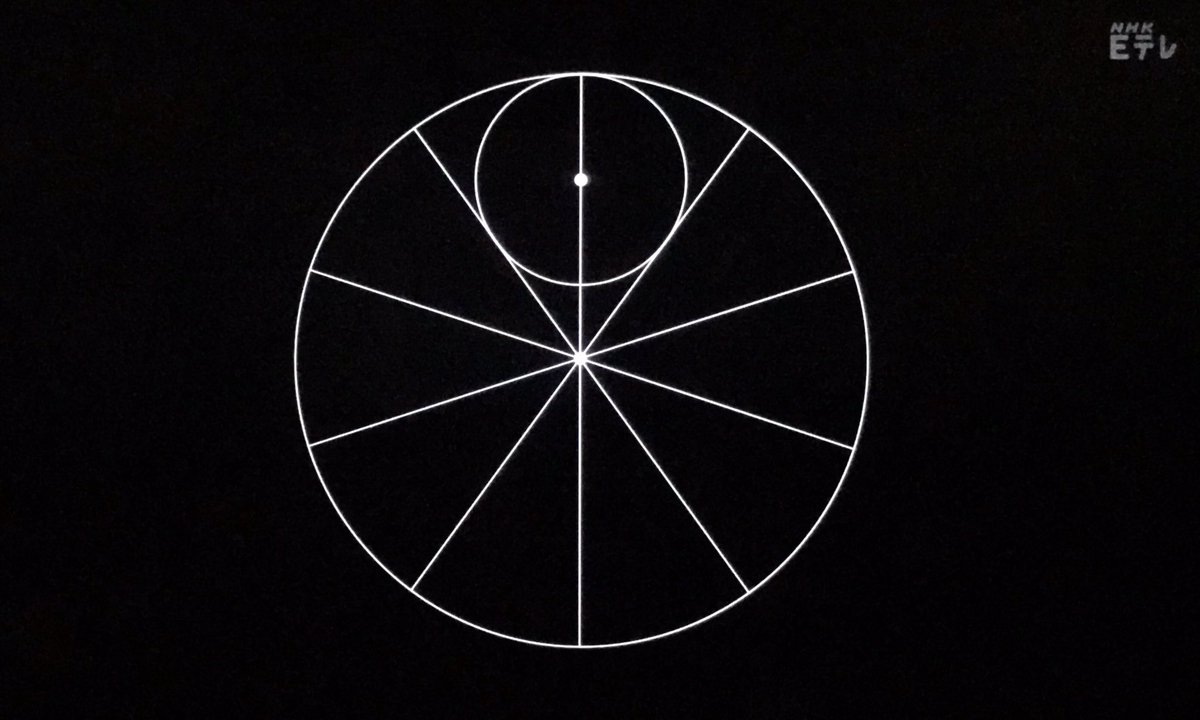
二つの円が交わる点と頂点を結んだ線が大きな円の半径と交わる場所を中心にして円を描きます。これがぴったり5個収まる円。 #デザインあ pic.twitter.com/zjtkouU9Ai
2020-01-03 09:54:25
拡大
拡大
拡大
rieco
@rieco_maracas
数式であらわすとこうです。 #デザインあ pic.twitter.com/yLpqF94Qgn
2020-01-03 09:54:33
拡大
拡大
拡大
拡大