-
 gandhara16
gandhara16
- 18266
- 10
- 5
- 1
 Tadas Nakamura 中村匡
@gandhara16
Tadas Nakamura 中村匡
@gandhara16
疑問:オイラー・ラグランジュ方程式を変分法で導くとき,部分積分をして端点での変分がゼロになるという条件をつかうが,これって必要? (続く)
2014-07-01 17:01:20 Tadas Nakamura 中村匡
@gandhara16
Tadas Nakamura 中村匡
@gandhara16
(続き)とえば,hooktail.sub.jp/analytic/verif… の式6の第一項だが,t_1< t <t_2を満たす t についてδq(t)はδq(t_1),δq(t_2)と独立だから,t の近傍では第一項は定数になって,(続く)
2014-07-01 17:05:08 Tadas Nakamura 中村匡
@gandhara16
Tadas Nakamura 中村匡
@gandhara16
(続き)境界条件からゼロにしなくても,t 付近の解を計算するときには寄与しない気がするのですが。もちろん,境界条件がないと解はきまらないけど,ローカルな方程式の導出にはいらないのでは?
2014-07-01 17:06:50 Tadas Nakamura 中村匡
@gandhara16
Tadas Nakamura 中村匡
@gandhara16
手近な力学の教科書をいくつかながめてみたけど,全部境界条件から第一項をゼロにしてた。しかし,こう見ると@irobutuさんの教科書はよくできてる。(あ,別に返信してくれって要求してるわけじゃないです,いやちょっとはそういうわけですけど。)
2014-07-01 17:10:08 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
一瞬、ここまでで「そうか」と納得しかけたんだけど、やっぱりどこか騙されている感が。実際のところ解を出した後で端っこを動かしてしまうと経路全部動いてしまうということを考えると、これで「ローカルな式は出ている」と納得していいもんだろうかと。 @gandhara16
2014-07-01 17:15:56 Tadas Nakamura 中村匡
@gandhara16
Tadas Nakamura 中村匡
@gandhara16
.@irobutsu さっそくのお返事ありがとうございます。期待以上の早さ! ローカルな式を出したあとで境界条件を,という流れならいいかもとも思うですが,なんかもやっとしてるのでちょっとよく考えてみます。
2014-07-01 17:22:17 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
試しに、時間を離散化した「Toy作用」を書いて途中の点で微分したら、確かに端っこ関係なしに運動方程式出ますねぇ。 しかしこれは離散化したことで部分積分がいらなかったからではないのかという気もするし。 @gandhara16 pic.twitter.com/15PHEeS2OB
2014-07-01 17:24:55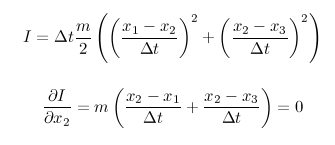 拡大
拡大
 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
端点を変分しないのは、「端っこ止めないと運動決まんないんだから、『運動を決めたい』という計算の主旨に反する」というのが話の筋として通っているんだと思います。では「運動決まら無くていいから運動方程式欲しい」という立場ならどうかという点が疑問ですね。 @gandhara16
2014-07-01 17:30:31 Tadas Nakamura 中村匡
@gandhara16
Tadas Nakamura 中村匡
@gandhara16
なるほど。「運動方程式+境界条件」をこみであつかうのが解析力学の趣旨だが,運動方程式だけなら端点の条件はいらないのかな? @irobutsu
2014-07-01 17:34:23 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
う〜ん、だんだん良いような気もしてきた。しかし「変分が独立なんだから真ん中のあたりの変分だけを考えて」というのは結局は「端っこを固定する」というのと同じ計算をやっているような気もしてきました。 @gandhara16
2014-07-01 17:55:32 Satoshi Yukawa
@s__w
Satoshi Yukawa
@s__w
@irobutsu @gandhara16 端を固定しないときには表面項が独立に0になるべしという条件から、固定境界条件でない別の境界条件が出てくるだけで、バルクは変わらないです。(中村さまお久しぶりです。)
2014-07-01 18:04:04 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
そういえば、正準方程式の方を変分原理で出す時(q,pを変数とする時)は、運動量pの方は一度も部分積分しないので、端点で運動量pの変分は0という条件はどこをどう見てもいらない。これは関係ない話か。
2014-07-01 18:05:34 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
その場合、端っこの「別の境界条件」の大本は何でしょう? つまりその条件は「何から導かれた」ことになるんでしょう?? ネーターの定理みたいに対称性が大本だった場合はそれが保存則に化けたりしますが。 @s__w @gandhara16
2014-07-01 18:07:49 Satoshi Yukawa
@s__w
Satoshi Yukawa
@s__w
@irobutsu @gandhara16 大本は、境界が変わりうることまで含めた最小作用の原理だと思います。例えば、端がある曲線上に拘束された懸垂線の問題とかも同じように解けますよね。
2014-07-01 18:15:39 TANIMURA Shogo
@tani6s
TANIMURA Shogo
@tani6s
横ヤリ失礼します。前野さん、ハミルトン形式(正準形式)の変分法では、両端の q は固定しますが、p は固定しません。部分積分した項に p の端点の変分が出て来ないという理由でよいと思います。@irobutsu @gandhara16
2014-07-01 18:16:32 TANIMURA Shogo
@tani6s
TANIMURA Shogo
@tani6s
例えば、アーノルドの本『古典力学の数学的方法』のp.236 に はっきりそう書いてあります。しかもそのページには端点の p を変化させている図まで描いてあります。@irobutsu @gandhara16
2014-07-01 18:18:34 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
@s__w @gandhara16 ああ、問題が「端っこが動いても作用が最小」である場合の話になるわけですか。なるほど。
2014-07-01 18:20:10 Satoshi Yukawa
@s__w
Satoshi Yukawa
@s__w
重力場中の運動で初期座標を固定しないときは、初速が0になるような条件が出てきますよね。@irobutsu @gandhara16
2014-07-01 18:20:16 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
@tani6s @gandhara16 どもども。あ、ちゃんと明記している本もあるんですね。実は「よくわかる解析力学」という本では、脚注にこそっと書いてあります(^_^;)。
2014-07-01 18:22:50 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
確かに初速度0という式が出ますね。それって「そうやると初速度0と出る」ということに直観的な理由ってつくんでしょうか?? 端点での微分は結局運動量だから、というのはわかるんですが…。 @s__w @gandhara16
2014-07-01 18:27:35 TANIMURA Shogo
@tani6s
TANIMURA Shogo
@tani6s
ラグランジュ形式では q の両端固定。ハミルトン形式で q, p 全部両端固定してしまうと、一般に微分方程式が解なしになってしまいますもんね。@irobutsu @gandhara16
2014-07-01 18:29:39 前野[いろもの物理学者]昌弘
@irobutsu
前野[いろもの物理学者]昌弘
@irobutsu
@tani6s @gandhara16 この端のpを固定しないってのは経路積分でも効いてます(そりゃ、量子力学でqを固定したらpは積分するしかないので)。
2014-07-01 18:34:49 杉田歩
@ayumu_sugita
杉田歩
@ayumu_sugita
@irobutsu @tani6s @gandhara16 横からすみません。「端点の変分が0になるという条件は必要か」という問い方にちょっと曖昧さがあると思います。端点の変分の条件がなくても、必要条件として運動方程式は出ますが、端点に対する変分も0とすると、一般には解なしに。
2014-07-01 18:35:50 杉田歩
@ayumu_sugita
杉田歩
@ayumu_sugita
@irobutsu @tani6s @gandhara16 だから、必要条件として運動方程式が出れば良い、という立場からすれば、端点変分の条件は考えなくてよいですが、実際に解が存在するような条件を考えたいなら、端点の変分は取らないことにする必要があります。
2014-07-01 18:37:17