阿原一志『作図で身につく双曲幾何学』を読む

{3,5/2} 大二十面体 @Polyhedrondiary

#GeoGebra が備える(円に関する)反転の機能を使って，双曲平面のポアンカレ円板モデルで遊んでみよう！という素敵な本。 PCでなくAndroid版をスマホで遊んでみたのだけど，Poincaré discは片手でも十分楽しめることが判明 twitter.com/Polyhedrondiar…

{3,5/2} 大二十面体 @Polyhedrondiary

【本棚登録】『作図で身につく双曲幾何学: GeoGebraで見る非ユークリッドな世界』阿原 一志 booklog.jp/item/1/4320111… #booklog

2018-07-03 05:00:02

{3,5/2} 大二十面体 @Polyhedrondiary

双曲平面のポアンカレ円板モデルってこういうやつ twitter.com/Polyhedrondiar…

{3,5/2} 大二十面体 @Polyhedrondiary

だまし絵で有名なエッシャーに「Circle Limit」っていう双曲充填の作品があるけど，もっとたくさんある彼の平坦充填の作品を双曲充填に変換するとこうなる！ Gallery : Hyperbolic Escher josleys.com/show_gallery.p… pic.twitter.com/WReMshjCEw

2017-09-23 08:26:55

{3,5/2} 大二十面体 @Polyhedrondiary

外側の円を理想円といって，この内側がポアンカレディスク。円板内は場所によって計量(縮尺)が異なり，同じ長さに見えても外側ほど双曲平面上の距離は長くなってて，理想円は無限遠点にあたる。 なのでこれらは全部同じ大きさの無限枚のタイルで敷き詰められてるってこと。 twitter.com/Polyhedrondiar…

{3,5/2} 大二十面体 @Polyhedrondiary

双曲平面は普通の平面と同じで無限に広い。 そして双曲平面の著しい特徴は，与えられた直線に平行で，その直線外の1点を通る直線が，無数にあるということ。すなわちそこでは非ユークリッド的な幾何学が繰り広げられる。

{3,5/2} 大二十面体 @Polyhedrondiary

双曲平面における直線は，理想円に直交する円弧又は線分(すなわち直径)で表され，図には互いに直交する2本の双曲直線CE,FGが描かれている。 双曲平面における円は，理想円内部の円で表され，図には点Aを中心とし，ABを半径とする双曲円が描かれている。 pic.twitter.com/QRX6pRpMbM

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

中心Aから双曲円までの距離は，双曲平面上では一定。そのように見えないのは，場所によって計量が異なるから。 一連の図において，AB=AD=半径となっていて，BCやDEは短く見えるけど長さ無限大。 pic.twitter.com/dHtG31SCiD

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

図の2本の双曲直線は双曲円と直交していて，ユークリッド幾何で円の中心を通る直線が円と直交するのと対応。 双曲平面上の互いに直交する2直線とその交点を中心とする円が，互いに直交し理想円とも直交する2円弧と，その双方に直交する円として描かれる様子を図示。 pic.twitter.com/TG5A6i0i3B

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

ポアンカレディスクに同心円を描いてみた。 内側4つの円は，点Aを中心とする半径1:2:3:4の同心円。 ABの中点がM，AMの中点がX，BMの中点がYです。 pic.twitter.com/QtlwEQiEI1

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

ポアンカレ円板モデルにおける等間隔な4つの同心円，動画版。 中心Aで直交している2直線は，これら同心円の直径を延長したもの。 pic.twitter.com/s8m1I7yYXF

{3,5/2} 大二十面体 @Polyhedrondiary

双曲平面上の円(双曲円)と，その直交する2直径を延長した直線(双曲直線)。gif版。 pic.twitter.com/QALGuKRCRq

{3,5/2} 大二十面体 @Polyhedrondiary

平行線公理が成り立たない非ユークリッド幾何学の1つ，双曲幾何学。 双曲平面は無数の平行線が引けることで有名だけど，「その代わり，平行な2直線の“双方に直交する直線”は1本しかないよ！」の図。 pic.twitter.com/UipPHKiPDN

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

至る所で曲率正なのが球面，至る所で曲率負なのが双曲平面。 前者では平行な直線の組は存在せず，後者では与えられた直線に平行かつその直線外の与えられた点を通る直線が無数に存在。 球面…平行線なし， 平面…平行線の双方に垂直な直線が無数に存在， 双曲平面…平行線の双方に垂直な直線は唯一つ pic.twitter.com/gSTWnSBaA5

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

双曲平面において，平行2直線の双方に垂直な直線はただ1つgif #GeoGebra pic.twitter.com/JChyufQkxO

{3,5/2} 大二十面体 @Polyhedrondiary

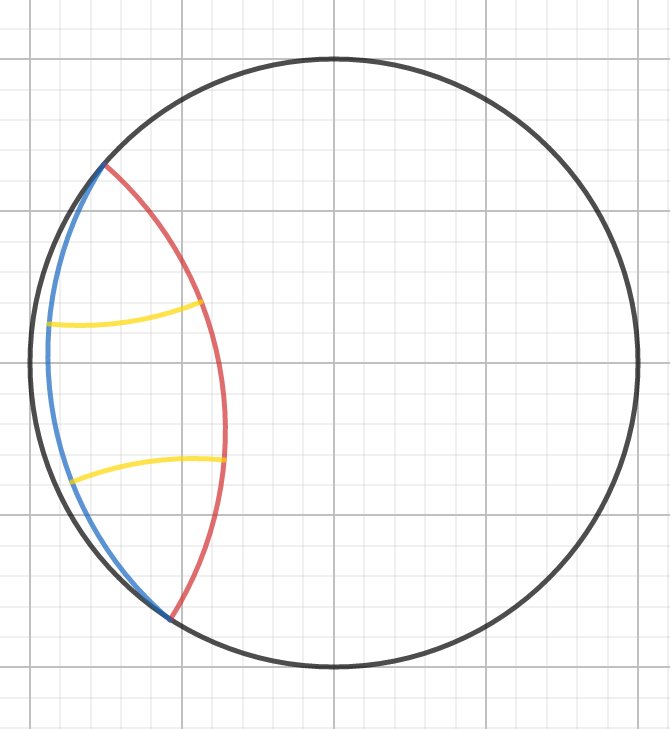
ユークリッド平面では2直線の間隔が至る所等しければそれらは平行だけど，双曲平面では2直線の間隔が至る所で等しいことはあり得ない。双曲平面上の2直線は，たとえ平行であっても間隔一定ではない。 与えられた直線(赤)との間隔(黄)が至る所等しいのは，双曲平面では直線ではなく曲線(青)になる。 pic.twitter.com/4CEXrxwvtP

拡大

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

赤も青もユークリッド的には円弧に見える。 でも赤は理想円(黒)と直交するから双曲平面上の直線(双曲直線)であるのに対し，青は直交しないので双曲直線ではない。 ちなみに黄は(その延長が)黒に直交する双曲直線で，さらに赤青にも直交するから赤青間の距離を表している。 pic.twitter.com/r5O7oTOK6c

拡大

拡大

拡大

拡大

{3,5/2} 大二十面体 @Polyhedrondiary

距離っていったい何だろう？幾何学の正体は？ とか普段まったく考えることのないことを考えられるので，非ユークリッド幾何学楽しい twitter.com/Polyhedrondiar…