数学2018年問題
-
- いいね！65
▼数学2018年問題
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ #math2018 2018年1月2日を織り込んだ（に出題するはずだった）割り算の虫食い算です。 nazopla.jp/quize/19848.ht… pic.twitter.com/5qGtEAA3Cv
2018-01-07 23:05:14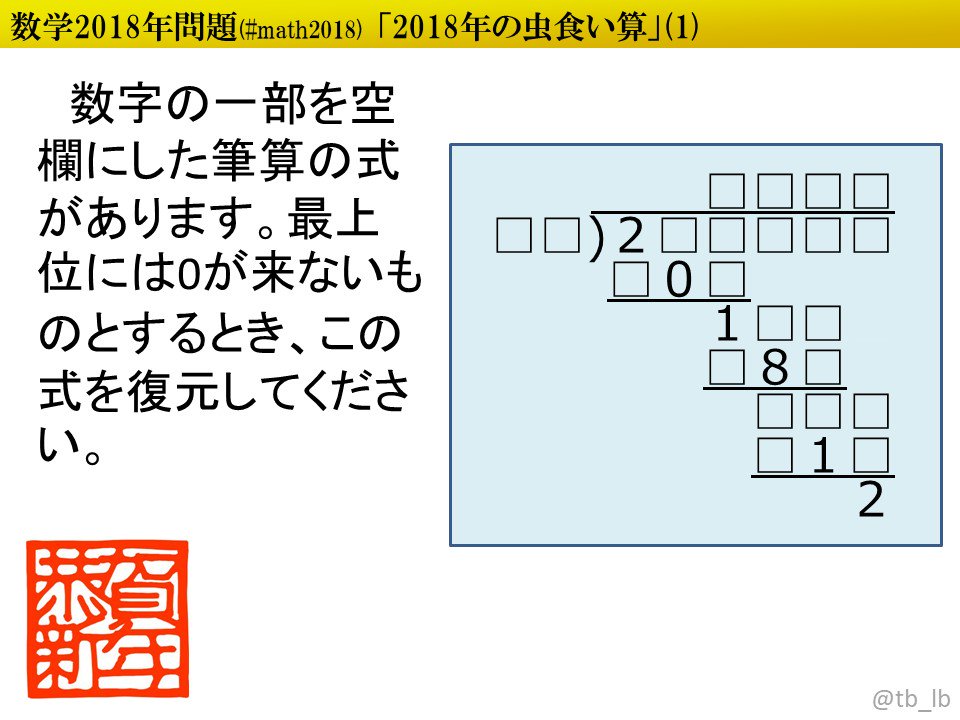
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ #math2018 2018年1月3日を織り込んだ（に出題するはずだった）掛け算の虫食い算です。 nazopla.jp/quize/19851.ht… pic.twitter.com/RePQcfRs0G
2018-01-07 23:26:44
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ #math2018 2018で割るとどの桁も0か1となる□□□2018□□□という形をした自然数は？ nazopla.jp/quize/19864.ht… pic.twitter.com/ekyj4sCrtV
2018-01-08 23:21:39
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ #math2018 分母分子が共に等差数列をなす分数列 2018/30, 2012/31, …, 2/366 で、値が整数となる項は？ nazopla.jp/quize/19925.ht… pic.twitter.com/LLHxIRA2uU
2018-01-21 23:54:28
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ #math2018 201820182018に＋を入れて作れる30の倍数のうち小さい方から3番目の数は？ nazopla.jp/quize/19955.ht… pic.twitter.com/VhBo5qdZr1
2018-01-28 23:50:54
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ 今週は図形問題をちょっとお休みして数列の問題をこしらえてみました。西暦を織り込んだ #math2018 となっています。 →ある分数列の第2018項の値 nazopla.jp/quize/20411.ht… pic.twitter.com/avCAU53dco
2018-04-08 23:49:19
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
#謎プラ #図形問題祭 第四夜！ 今夜は変化球ということで座標平面上の図形がテーマです。欲張って西暦も織り込んで #math2018 仕立てにしてみました。計算をどこまで減らせるでしょうか。 →不等式で表される図形の面積関係 nazopla.jp/quize/20682.ht… pic.twitter.com/3vyvHGORrm
2018-05-31 22:00:07
拡大
くす394
@kusu394
早速2018年の問題です a+b=2018を満たす正の整数a,b(a≧b)について、 a,bの各桁には高々2種類の数字しか現れないと言う このとき、aとbを求めよ
2018-01-01 00:03:35
くす394
@kusu394
もうひとつ2018を使った数学の問題を a+b=2018を満たす2以上にの正の整数a,bについて a-1とb-1の最大公約数として考えられるものはいくつあるか
2018-01-01 00:06:09
くす394
@kusu394
最後 座標平面でx,yが共に整数である点のことを格子点という。 格子点を頂点とする5角形であって その内部(周上を含まない)に格子点が2018個あるものを考える。 このような5角形の面積の最小値を求めよ。
2018-01-01 00:11:09
飛鳥
@Asuka_Tsukimi
新年初のパズルです．是非解いてください(*^^*)(*^^*) はてなブログに投稿しました #はてなブログ 2018 - パラボリック・パズル parabolic-puzzles.hatenadiary.jp/entry/2018/01/…
2018-01-01 01:46:26
実用数学技能検定「数検」
@sugaku_net
【HAPPY NEW YEAR 2018】あけましておめでとうございmath。本年も「数学検定」「算数検定」をどうぞよろしくお願いいたしmath！みなさまにとって素敵な1年になりますように。ここで、2018年最初の問題！ pic.twitter.com/vIdknNXvUh
2018-01-01 08:00:02
拡大
tb_lb／日曜夜に補助線主体の図形問題の再出題やってます
@tb_lb
【年賀パズル情報】２０１８年賀パズル: 算数の広場 ksik-math.seesaa.net/article/455715… ★戌年にちなんだ裁ち合わせパズルや定番の算数パズルが出題されています。
2018-01-01 13:29:29
RYU＠新作考案中
@MandR_Trovi
明けましておめでとうございます。 毎年恒例の年賀状パズルです。 印刷した方が考えやすいと思いますが、とりあえず。 pic.twitter.com/BQmgxbHhrF
2018-01-01 13:36:03
拡大
開成数学研究部
@KsSuken
#今日の一題 2018にちなんだ1問を。 2018のように、各位の桁の和と各位の桁の積の差が11であるような4桁の整数の個数を求めよ。 (部内模試より) DMにて解答をお待ちしております！
2018-01-01 15:35:30
James Tanton
@jamestanton
Is it possible use each of the digits 2,0,1, and 8 at least once to fill a 4x4 grid so that each row, col and the two diags have the same sum? Do this with each digit appearing exactly four times? Do either of these without worrying about the diags?
2018-01-01 22:40:51
数学問題置き場
@HimaginaryMp
【作者は答えを真面目に考えてすらいないけど正月に便乗したかったからとりあえず投下するシリーズ】 自然数に対して関数f(x)を次のように定める； ・f(x)=x/2(xは偶数) ・f(x)=3x+1(xは奇数) a_1=2017、a_(n+1)=f(a_n)とするとき、数列{a_n}に2018は現れるか
2018-01-02 01:27:48