
「移項」とは一方の辺の項を符号を逆にして他の辺に移すこと ←何だこれ?
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 添付画像はNHK高校講座ベーシック数学 nhk.or.jp/kokokoza/tv/ba… より 添付画像のような教え方をするから、教わった子がダメになるのだと思う。 「同じものに同じ操作をしても同じまま」という当たり前に原理さえ認識しておけば「移項」という用語は不必要になる。 pic.twitter.com/L2Bm2CbXzt
2018-05-19 00:56:42 拡大
拡大
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 他のPDFも酷い。 「覚えなければいけないことはほとんどないのに、ものすごく役に立つ」という数学的思考の美味しい部分は一切教えられず、覚える必要がないことを曖昧で不完全な説明で次々に覚えろと言われる分野になっているんじゃないか?
2018-05-19 00:56:43 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 「a + b = c のとき、その両辺から b を引くと a = c - b が得られる」なら、何をやっているかが明瞭で、「b≠0のとき、ab=c の両辺をbで割ると a=c/b が得られる」に自動的に一般化される。等式の変形の基本は「同じものに同じ操作を施しても同じまま」という当たり前のこと。
2018-05-19 01:03:31 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 これを「左辺の b を右辺に移項すると -b になる」のように教えるから、「え?どうして?」となってしまう子が当然出て来る。 覚える必要がないくだらないことは、「くだらない」とはっきり生徒に伝えることが大人の甲斐性だと思う。
2018-05-19 01:03:31 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 ちなみに、NHK高校講座ベーシック数学 nhk.or.jp/kokokoza/tv/ba… での多項式の定義の説明は添付画像の通り。酷すぎ。 この国の算数・数学教育は結構酷い。 保護者的にはものすごく参ってしまう。 pic.twitter.com/se0EdlJ4Wg
2018-05-19 01:09:13 拡大
拡大
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 「文字をアルファベット順に並べて整理することもあるし、そうしないこともある」程度の話でしかないのに、勝手にルールにしちゃっているし。 まあ、チョー算数に頭が侵されている人が作ったものなので、勝手にローカルルールを捏造するのも仕方がない。 nhk.or.jp/kokokoza/tv/ba… pic.twitter.com/2T3Opr0Czv
2018-05-19 01:16:29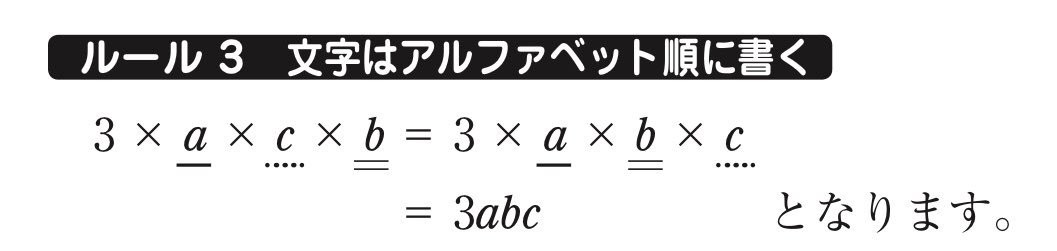 拡大
拡大
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 いやあ、びっくらこいた。 倍数の説明もチョー算数(=教科書的算数)と同じ「0は除く」のスタイルに見える。 これだと「4の倍数であることと、下2桁が4の倍数であることは同値」と言えない。これ、高校の数学講座です。 nhk.or.jp/kokokoza/tv/ba… pic.twitter.com/jiDpZWMUbn
2018-05-19 01:22:39 拡大
拡大
 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
#超算数 このような教育を受けても、当たり前の原理(例えば「同じものに同じ操作を施しても同じまま」とか)に戻ってシンプルに考えることとか、論理的な考え方とか、数学の美徳とされていることは何一つ身に付かないと思う。 楽しくないし、下らないし、情けなくなるような話。
2018-05-19 01:26:17 積分定数
@sekibunnteisuu
積分定数
@sekibunnteisuu
@genkuroki #超算数 突っ込みどころ満載ですね。 整数の素因数分解と多項式の因数分解がごちゃごちゃ nhk.or.jp/kokokoza/tv/ba… >2x + 2y を因数分解すると、 2x + 2y = 2(x + y) となります。 6x+6yを因数分解は3・2(x+y)とすべきなのか?
2018-05-19 01:29:09 積分定数
@sekibunnteisuu
積分定数
@sekibunnteisuu
@genkuroki #超算数 ベーシックならむしろ、公式を使わないで分配法則を使って展開したほうがいいと思うが・・・ nhk.or.jp/kokokoza/tv/ba…
2018-05-19 01:31:13 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki その操作をどう理解するかとは別の問題として、授業中に先生が板書しながら「この項を移項すれば・・・」と話している時に言葉が通じないのは困るので、移項という言葉を覚えること自体がくだらないと断じては誤解を生むのではないでしょうか。
2018-05-19 08:04:49 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi 生徒には「歴史的な不幸な偶然のせいで、『移項』という不必要で誤解を招く数学用語が広まってしまっている。そういう用語を繰り返し使う困った数学教師のために『移項』という用語も仕方無しに一応覚えておきましょう(笑)」とでも教えておけばよいと思います。続く
2018-05-19 08:31:28 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi さらに「a+b=cをa=c-bに変形することは、左辺の項bを-bに変えて右辺に移動しているのではなく、a+b=cの両辺からbを引いているだけ。等しいものに同じ操作を施しても等しいままになるという当たり前のことを使っているだけ。『移項』という用語にはこのシンプルな事実を見えなくする悪い面がある」と。
2018-05-19 08:36:22 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi そして「『移項』に限らず、数学用語の多くが、歴史的偶然によって広まってしまった悪しき用語になっているので、用語の暗記を強要するダメな数学教師には注意するように。私が間違って『移項』という用語を授業で使ってしまったら、『先生、移項って言わない約束でしょ』と注意して下さい(笑)」と
2018-05-19 08:40:18 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi で、実際に授業時間に先生の側が「移項」と言ってしまって生徒達が大笑いすると。ここまで頑張ったら、生徒は色々なことを学んでくれるんじゃないですかね。 「移項」という用語のよろしくない点と正しい考え方と、非本質的な用語の暗記にこだわる数学教師がダメであることを学んでもらえる(笑)。
2018-05-19 08:44:10 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi 真っ当な数学教師なら「a+b=cのbを移項すると、a=c-bとなる」と言わずに、「a+b=cの両辺からbを引くと、a=c-bになる」と言ってくれるものだと思います。 わざわざ誤解を招く「移項」という用語を数学初心者の生徒に対して無神経に使うのはやめるべきだと思います。
2018-05-19 08:48:01 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi 中高生には、「移項」という用語を暗記することがどれだけ下らない行為であるかを強調した方が、結果的に「移項」という用語を覚えてもらい易いのではないかと思います(笑)。
2018-05-19 08:51:02 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki a+b+c を c+b+a に変形できるのは、a と c とを入れ替えているのではなく、a+b を b+a とし、a+c を c+a とし、b+c を c+b としているだけ。和の交換法則を使っているだけ。任意の項を入れ替えられる、と教える(覚える)ことはこのシンプルな事実を見えなくする悪い面がある、とはならないような。
2018-05-19 08:59:35 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki 暗算などで無意識に使うような、ある意味当たり前な演算定理を明示して、時には名前を付けて教えることには利点も多いと思います。「a と c とを入れ替えて」と言う代わりに「交換法則を3回使って」と言った方が良いとは思えないです。
2018-05-19 08:59:57 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki 例が悪かったらすみません。でも、「両辺から b を引く」ではなく「左辺の b を右辺に移す」と考えることで計算能力が飛躍的に上がるのは間違いありません。その点を無視した議論になっているのではないかと危惧しました。
2018-05-19 09:04:43 黒木玄 Gen Kuroki
@genkuroki
黒木玄 Gen Kuroki
@genkuroki
@osamu_takeuchi 【例が悪かったらすみません。でも、「両辺から b を引く」ではなく「左辺の b を右辺に移す」と考えることで計算能力が飛躍的に上がるのは間違いありません。その点を無視した議論になっているのではないかと危惧しました。】 おバカなことは言わない方が良いです。
2018-05-19 09:08:52 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki もう1つ、「誤解を招く」というところが分かりませんでした。誤解を招く説明がされていることとは別にして、「移項」という語を使うこと自体がまねく誤解とは、どういった内容を指しているのでしょうか?
2018-05-19 09:09:24 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki 「移項」は「等号の反対側に項を移すための定理」で、式変形を効率的に行うのに覚えておくと便利、という認識を持つ人は多いと思いますし、私もそう思います。数学にも覚えておくと便利な定理はたくさんあって、どれを採用するかには任意性があります。「移項が生みかねない誤解」について論じずに
2018-05-19 09:24:18 武内 修
@osamu_takeuchi
武内 修
@osamu_takeuchi
@genkuroki リンク先の説明が悪いこととごちゃ混ぜに議論されているように思います。「移項」という語を使うこと自体の弊害について教えて下さい。
2018-05-19 09:27:22