潮汐力と遠心力を巡るよくある誤解を巡るよくある（？）議論
-
- いいね！0
ぼんてんぴょん(Bontenpøn)
@y_bonten
つい1か月前に松田卓也先生が潮汐力について書かれていて、そこでは半田利弘先生の記事を「誤解の根源」としている。 また楽しみが増えた。 http://t.co/TN8K3E0cTs …
2013-09-06 12:09:54
ぼんてんぴょん(Bontenpøn)
@y_bonten
松田卓也先生の記事（ http://t.co/TN8K3E0cTs ）、「地球重力に組み込まれる」ってどういうこと？と期待して読んでいたら「そんな人に説明するのは、ほんとうに疲れる」で終わっている。見捨てないでぇ～
2013-09-06 12:35:53
ぼんてんぴょん(Bontenpøn)
@y_bonten
@irobutsu先生、@AXION_CAVOK先生、筋違いかとは思うのですが、松田卓也先生の潮汐力の記事（ http://t.co/TN8K3E0cTs ）が完全には理解できず、正しいかどうかも判断できないので、どうかお時間のあるときに目を通していただければ幸甚です。
2013-09-06 13:13:40
ぼんてんぴょん(Bontenpøn)
@y_bonten
そもそも俺が遠心力について理解を深めることができたのは松田卓也先生の http://t.co/Ptt3Hc1y0y のおかげなのだ。なのに、同じ先生の遠心力の解説で分からなくなるなんて・・・。
2013-09-06 13:19:06
前野［いろもの物理学者］昌弘
@irobutsu
ふ〜む（←読んでる）RT @y_bonten ：@irobutsu先生、@AXION_CAVOK先生、筋違いかとは思うのですが、松田卓也先生の潮汐力の記事（ http://t.co/U3gcVnFJzO … ）が完全には理解できず、正しいかどうかも判断できないので、【略】
2013-09-06 16:53:51
前野［いろもの物理学者］昌弘
@irobutsu
図３の理屈が正しいことはわかるけど、だからといって図４が間違っているという根拠がよくわからないなぁ。二つの説明のどっちもそれでいいんじゃないの、と思ってしまうのだが。 @y_bonten @AXION_CAVOK
2013-09-06 17:04:45
ぼんてんぴょん(Bontenpøn)
@y_bonten
@irobutsu @AXION_CAVOK ありがとうございます。遠心力としては図4が正しいけれども、潮汐力に関与するのは図3、という論旨だと思うのですが、よく理解できていません。
2013-09-06 17:21:28
前野［いろもの物理学者］昌弘
@irobutsu
「地球重力に組み込まれる」ってのは、点Pで働く遠心力は 共通重心からPへのベクトル＝地球中心からPへのベクトル＋共通重心から地球中へのベクトル になるけど第1項は重力に比例するからまとめちゃえ、ってことかと。@y_bonten @AXION_CAVOK
2013-09-06 17:22:59
前野［いろもの物理学者］昌弘
@irobutsu
潮汐力は「力の場所による変化」で現れるけど、遠心力の「場所による変化」はちょうど重力に組み込まれる部分だから、実は遠心力（の変化）は潮汐力には寄与してない、という理屈みたい。 @y_bonten @AXION_CAVOK
2013-09-06 17:25:22
前野［いろもの物理学者］昌弘
@irobutsu
私の好きな潮汐力の説明は、 赤：万有引力 緑：遠心力 青：合力 とポテンシャル描いて、平衡点の両側では離れる方向に力働く、みたいにやるから「遠心力は関係ない」と言われるとちと違和感。 @y_bonten @AXION_CAVOK http://t.co/37e5x9WPnM
2013-09-06 17:37:10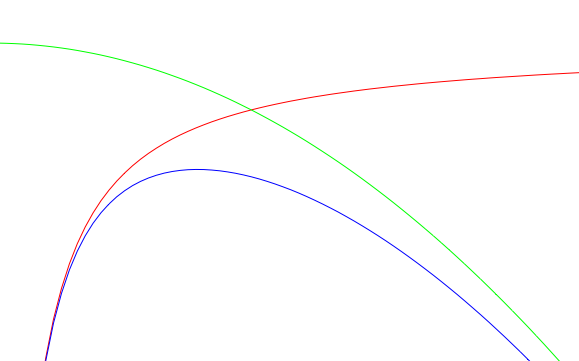
拡大
あ〜る菊池誠(反緊縮)公式
@kikumaco
@irobutsu @y_bonten @AXION_CAVOK 僕も潮汐力の説明は万有引力と遠心力の合力だなー。ラリーニーブンの「中性子星」
2013-09-06 17:39:41
前野［いろもの物理学者］昌弘
@irobutsu
違和感はあるけど、松田さんの説明が間違っているというわけではないです。あの図３の説明はそれはそれで筋は通っているし、実は遠心力から地球の重力に組み込まれる部分を引いちゃうと定ベクトルだというのはなかなかおもしろい。 @y_bonten @AXION_CAVOK
2013-09-06 17:41:09
ゆ〜たん💉💉💉💉💉💉💉
@Iutach
@kikumaco @irobutsu @y_bonten @AXION_CAVOK 確かアシモフは月の重力だけで説明してました。
2013-09-06 17:52:39
ピンちゃん（自宅警備中）
@ping_chang
@irobutsu @y_bonten @AXION_CAVOK そう言えば、書棚に坪井忠二先生の『重力』というのがあったなと思いだし、目次をみてみたら、潮汐論に関する言及はないみたいでがっかりしました。昔はどういう具合に説明していたのか期待していたのですが。。。
2013-09-06 18:00:02
AXION
@AXION_CAVOK
@y_bonten @irobutsu 仕事してたら出遅れた(^_^;)。 図4も地球の重力を入れて無いだけで、間違いとまでは言えないと思います。 ただ、見かけの力を使うとややこしくなるのは間違いないので、松田先生としては、向心力だけで考えればいいじゃん……と言う意図でしょう。
2013-09-06 18:52:22
ぼんてんぴょん(Bontenpøn)
@y_bonten
@irobutsu @AXION_CAVOK ありがとうございます。ご教授をもとに、延々と考えておりました。記事が誤っていないことはおおむね理解できました。
2013-09-06 21:11:41
ぼんてんぴょん(Bontenpøn)
@y_bonten
@irobutsu @AXION_CAVOK 各地点において、地球中心から外向きの方向を正として潮汐力を比較するときに、「地球中心に向かい、大きさが等しい力」（その代表が地球重力）は初めから一律に差し引いて考えているわけですね。
2013-09-06 21:12:15
ぼんてんぴょん(Bontenpøn)
@y_bonten
@irobutsu @AXION_CAVOK ベクトルCAは、わざわざ「地球重力に組み込める」と言わなくても、「大きさがどの地点でも等しく、地球中心に向かうベクトルなので、潮汐力の比較に影響しない」と言えば済みますね。たまたま地球重力も同様の性質を持っているけれども。
2013-09-06 21:13:21
ぼんてんぴょん(Bontenpøn)
@y_bonten
半田先生の発想は、潮汐力を、「単位質量の粒子を地表につなぎとめておくために必要な力」（にマイナスをつけたもの）と考える、というものだ。この重大な発想が記事中に明記されていない点が、一番痛いところ。私もメールで質問をして初めて理解した。
2013-09-06 21:25:08
ぼんてんぴょん(Bontenpøn)
@y_bonten
この点を考えると、松田先生が「試験粒子は系で静止しているべきなのでコリオリ力云々はナンセンス」と批判するのも無理はない。
2013-09-06 21:26:22
近く本朝を窺うに、平成のゼルプスト殿下
@tenapi
@y_bonten 潮汐力というのは、保存力の場で運動している剛体の運動が重心位置にある点質量に準じた動きをしているために、剛体上のそれ以外の位置で、ポテンシャルから受ける力に対して生じるお釣りのようなもの、と理解しておるぞよ。
2013-09-06 21:43:07
AXION
@AXION_CAVOK
@y_bonten @irobutsu 今更ながらだけど、図4は回転系と言いながら、月の重力（緑線）がキッチリ書いてあるのが問題ですね。 意図的に抜いてある気がするけど（こういう風に間違えるという意味で）、G点では黒線は無くても、緑線があることになってしまって、それは矛盾。
2013-09-06 22:06:32
やせごんぼ
@Yase_Gombo
@y_bonten 横槍失礼します。松田先生の説明は、月と地球の公転中心を中心として全ての点が回転していると考えており微妙です。このような状況は月の公転と地球の自転が同期している場合にしか起こらず、現実を表していません。
2013-09-06 22:29:36