和算〜江戸時代の連中は、なんちゅう計算をそろばんでしとるんだ〜

佐藤賢一の中の人 @ke_1sato

計算が袋小路、役所広司

佐藤賢一の中の人 @ke_1sato

江戸時代の連中は、なんちゅう計算をそろばんでしとるんだ、とひとしきり

佐藤賢一の中の人 @ke_1sato

弓形の弧長を求めるために関孝和は、 arccos^2 (24/25)≒0.0805390964213483117、 という値を、分数 200860100457／2493945312500≒0.0805390958054538 で近似している。何桁の連分数を展開してるんだあ！と悶絶

佐藤賢一の中の人 @ke_1sato

めちゃくちゃ精密な近似である。(もちろん真値が分かれば連分数そのものは難しい計算ではないし、近似が精密になるのは当然なのだが。。。)これをどうやって見つけたんだ!!!、というのが今の課題。10^(-10)のオーダーで近似するとはね。 pic.twitter.com/YTteV1mptE

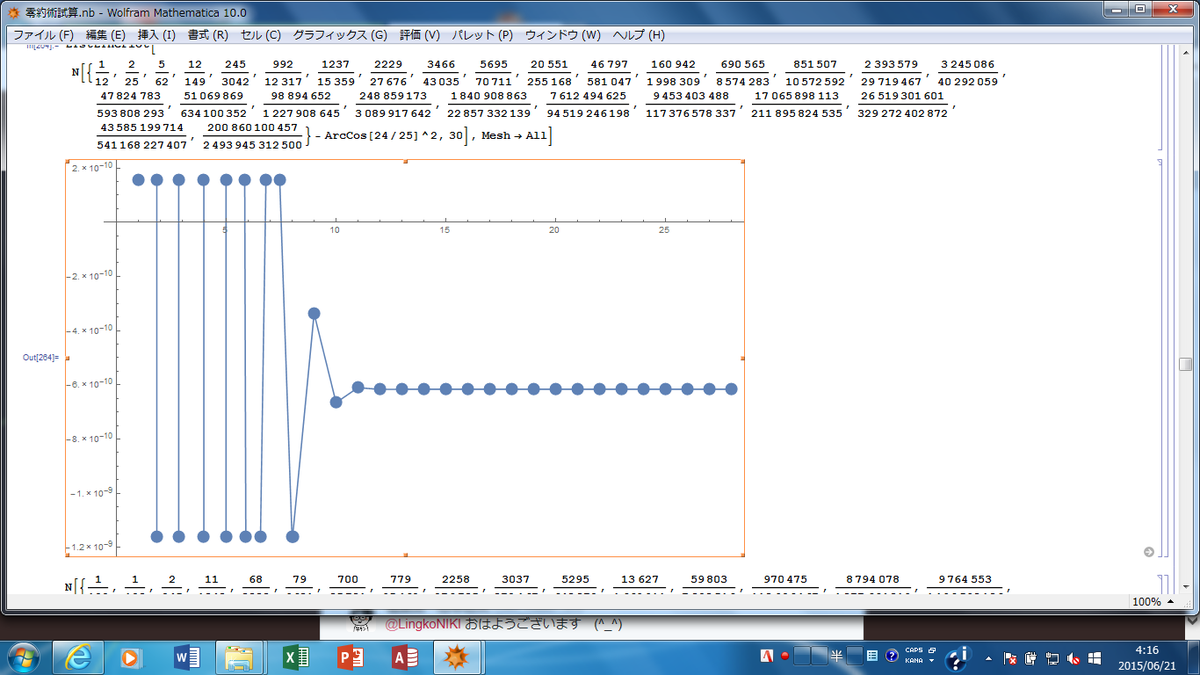拡大

佐藤賢一の中の人 @ke_1sato

ちなみに先ほどの分数の分母は 2493945312500=2^2＊5^11＊113^2　と素因数分解できる。この113という素数はπ=3.1415…を355/113で近似したことからおそらく説明可能。一方、分子の素因数分解は3＊66953366819となり、11桁の素数が出現w

佐藤賢一の中の人 @ke_1sato

素数66953366819は、もしかしたら和算家が計算した素数の中では一番大きな値かもしれない。ただし、偶然たどり着いた計算結果だろうから、これを素数と意識していたかどうかは怪しい。(和算家たちは素数のことを｢単数｣と言っていた。)

佐藤賢一の中の人 @ke_1sato

他にも関孝和が近似した数値は以下。 arccos^2 (4/5)≒2974254163 / 7182562500 arccos^2 (3/5)≒686235249 / 798062500 arccos^2 (7/25)≒4130907926451 / 2493945312500

佐藤賢一の中の人 @ke_1sato

むちゃくちゃである。

佐藤賢一の中の人 @ke_1sato

これをそろばんで計算していたとか

佐藤賢一の中の人 @ke_1sato

関孝和のやったことを｢数学｣としては理解できるのだが、｢歴史｣として見ると、まだ説明はつかない。今まで悩んでいたのは、数学のテクニックとしては｢連分数｣を使っていたのかな？ということ。予想はできていたのだが、1680年代にそれができていたのか？という疑問が、歴史の問題となる。

佐藤賢一の中の人 @ke_1sato

つまり、関孝和が連分数を使えた証拠のような物があれば、議論はかなり進展する。(全部解決とはいかないまでも。)最近、関孝和と同時代で、しかも彼と交流があったかもしれない和算家の史料に連分数と同じ計算技法があったことを確認したので、関がこれを使っていても不自然ではないな、と分かった。

佐藤賢一の中の人 @ke_1sato

そもそも、さっき話題にした関孝和の計算結果は、平成になってから自分が数学ソフトを使ってその近似の精度を確かめたもの。それまでは、その式は形式だけを見て数学的に間違っているはずと言われ、検算すらされてこなかった。ただ、それも仕方ないことで、電卓が使えてもこんな数値は扱いたくないw

Kenichi Tomura/戸村賢一 @kenichi_tomura

@ke_1sato 何百人もで手分けしてやってた可能性はどうなんでしょうか？ 一人でやるもんじゃなさそうなので・・・

佐藤賢一の中の人 @ke_1sato

当時の状況を考えると、計算のできる人を集められても、良くて数名程度でしょうか。 RT @kenichi_tomura 何百人もで手分けしてやってた可能性はどうなんでしょうか？ 一人でやるもんじゃなさそうなので・・・

Kenichi Tomura/戸村賢一 @kenichi_tomura

@ke_1sato ではあまり分業しても効果なさそうですねw 和算の人って根性アルというかなんというか・・・オイラーやガウスとは全然別なベクトルですごいことやってるんですね・・・

佐藤賢一の中の人 @ke_1sato

まあ、そのことについて考えていない時間の方が圧倒的に多かったけれども、20年前から気になっていた歴史的問題も、史料さえ出てくれば1週間で一気に解決の手前まできてしまう。それが歴史研究の面白いところではありますね。

佐藤賢一の中の人 @ke_1sato

ああ！まさに彼の名前を出すのがピッタリかもw twitter.com/gesrausesl/sta…

RIG-026N1 @gesrausesl

ラマヌジャン的な(笑) twitter.com/ke_1sato/statu…

2015-06-21 05:37:40

Tomohiro Takata @wingcloud

@ke_1sato でも連分数を使うと分母分子を求めるアルゴリズムに足し算が入るので、分母の素因数に法則性が見えるのが不思議な気がするんですが、なぜ連分数が使えるといいんでしたっけ？

Kenichi Tomura/戸村賢一 @kenichi_tomura

@ke_1sato 全然門外漢からの質問なのですが、和算が廃れたのって、西洋数学の影響ってあるんでしょうか？ 18世紀になると解析学も幾何学もすごい発展しますので、オランダ経由でそれが届いて打ちのめされちゃったとか・・・

佐藤賢一の中の人 @ke_1sato

それで、まだ一意にアルゴリズムを確定できていないんですが、どうもπの補正計算を後からしているようで、必ず113が分母に因数として紛れ込んでいるんです。 RT @wingcloud でも連分数を使うと分母分子を求めるアルゴリズムに足し算が入るので、分母の素因数に法則性が見えるのが

Tomohiro Takata @wingcloud

@ke_1sato なるほど…5のべきがやけに多いのも気になりますね。

abigail9821（月光蝶であるＸ） @abigail9821

@ke_1sato ラヌマジャンの計算能力には、未だよくわかっていない部分があるんですが（要は、彼は一瞬で、複雑な計算を要するはずの答えにたどり着いていたように見える事が何度もあったようなので）…もしかしたら、関孝和もこの能力を持っていたのではないでしょうか？

佐藤賢一の中の人 @ke_1sato

たしかに、そんな能力があったのではないかと思わせるような計算結果は幾つかありますね。 twitter.com/abigail9801/st…

佐藤賢一の中の人 @ke_1sato

関孝和の４～50年後の世代になると一つの塾で数十人の門人を抱えるような規模になるのですが、彼の頃はちょうどブームの先駆けで、マニアの数をそろえるのは逆に難しかった頃合いですね。それでも有能な弟子がいたのが関にとっては幸いでした。 twitter.com/gesrausesl/sta…

RIG-026N1 @gesrausesl

関孝和のころは和算の隆盛期で無数の愛好家の結果を流用できた可能性は否定できないのではないでしょうか。 twitter.com/ke_1sato/statu…

2015-06-21 06:05:17

佐藤賢一の中の人 @ke_1sato

そうそう。江戸時代にも数学の通信添削システムはありましたからね。 twitter.com/motoaki_226/st…