-
 paraparaporu
paraparaporu
- 251146
- 162
- 168
- 184
 鈴木貫太郎
@Kantaro196611
鈴木貫太郎
@Kantaro196611
視聴者の塾の先生から「某中学校の定期テストの過去問を見て困った」どう答えればいいのでしょうかという質問。常に「どうしてそうなるかを考えることが大事」と言っているオイラも、流石にこの「なぜ?」には困った。模範解答を募集します。 pic.twitter.com/MK8OVIeUHF
2019-06-09 01:05:34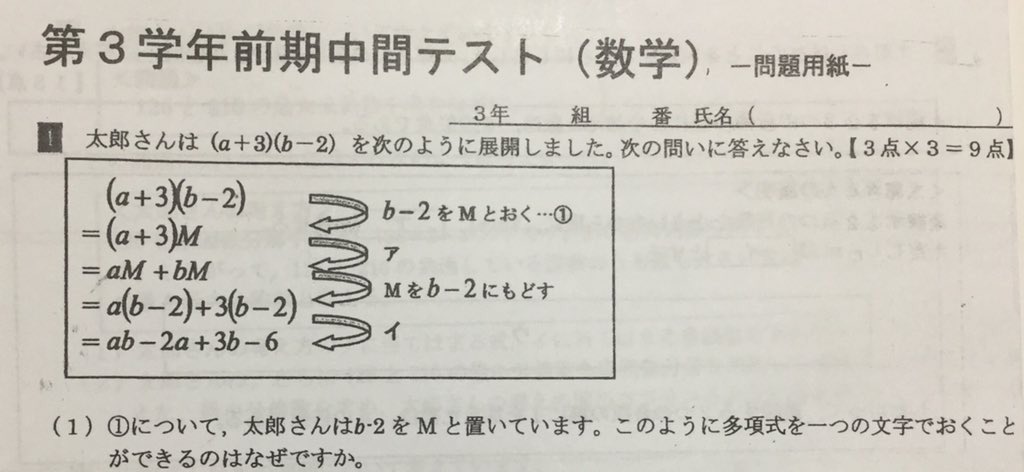 拡大
拡大
 荒木秀典| インプロバイザー
@garireo_1204
荒木秀典| インプロバイザー
@garireo_1204
@Kantaro196611 bは実数であるから、b-2も実数となる。ここでb-2の値は実数Mを用いてM=b-2と書き表すことができる。 のようような答えはどうでしょうか?
2019-06-09 01:18:22 荒木秀典| インプロバイザー
@garireo_1204
荒木秀典| インプロバイザー
@garireo_1204
@nao159635741251 @Kantaro196611 確かにそうですね ならこのよう添削してみるとどうですかね? bは何かしらの数が入るはずである。ここでb-2の計算結果をMと書くことにするとM=b-2と書き表すことができる。
2019-06-09 10:17:27 tecchan
@tecchan63729520
tecchan
@tecchan63729520
@Kantaro196611 多項式とは冷凍室でbと-3が凍って一体になった物でこれをMと名付けておき、後で他の食材と掛け合せて煮込めば、bと-3を冷凍せずに煮込んだ料理と結果は同じになるから (私も塾講してますが、例え違っていても楽しい話の方が理解され易いと思います)
2019-06-09 05:33:55 これからとにかくでかくなる会長
@estylevmacihne
これからとにかくでかくなる会長
@estylevmacihne
@Kantaro196611 @by_xun_kuang 問い方は悪い気がしますが、伝えようとしていることはわからなくはないですね。 勉強が苦手な生徒に見られる2✖√3を√6と答えたり、(a+b)^2をa^2+b ^2と答えてしまったりする子に共通するのは、√3や(a+b)が何か具体的な数値(M)として扱われうるという認識の欠如だと思います。
2019-06-09 09:59:11 これからとにかくでかくなる会長
@estylevmacihne
これからとにかくでかくなる会長
@estylevmacihne
@Kantaro196611 @by_xun_kuang パッと具体例が浮かばず分かりづらい例示になってしまいましたが、生徒を指導しているとしばしば上記の通り感じます。 それに対する先生なりの対策なのではないのかと勝手に思っております。 模範解答ではないですが、悪しからず。
2019-06-09 10:06:19 石戸@医師×経営者
@YusukeIshito
石戸@医師×経営者
@YusukeIshito
@Kantaro196611 面積を使って説明するというのはどうでしょうか?? (a+3)(b-2)は一辺の長さがa+3とb-2の面積を表し a+3の辺をaと3に分けると、 面積は、a(b-2)+3(b-2)とも表せる。 このように、どんな多項式でも、一辺の長さと 捉えることができるから、 多項式を一つの文字でおくことができる pic.twitter.com/cPnIjy6AZ4
2019-06-09 02:37:59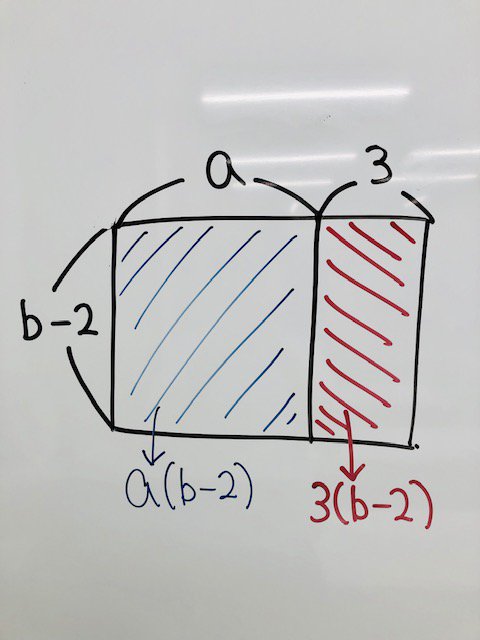 拡大
拡大
 数学 for 大学受験
@Mathworld4
数学 for 大学受験
@Mathworld4
@YusukeIshito @Kantaro196611 コメント失礼致します。 a>0かつb>2という条件がないのでそれでは一般性を失ってしまいます。したがって任意の多項式に対して成り立つとは言えないかと…
2019-06-09 02:48:45 寝子(*˘︶˘*)
@kgAmJ259physics
寝子(*˘︶˘*)
@kgAmJ259physics
@Kantaro196611 a,bを定数とし、a-bという式を考える。ここで、a-bは定数であるから、これを定数Mと等しいものとすれば、a-b=Mと表せる。また、L,Nを定数とし、N=L-Mと表せるとすると、N=L-a+bである。従って、これを繰り返すことにより、項の数によらず、多項式は1つの文字で表せることが示される。 でしょうか…?
2019-06-09 01:55:52 寝子(*˘︶˘*)
@kgAmJ259physics
寝子(*˘︶˘*)
@kgAmJ259physics
@Kantaro196611 またこれは、aまたはbまたはその両方が変数であったとしても、a-bに対応する値をMと置くことにより、同様のことが言える。 入りきらなかったので付け足しましたm(_ _)m
2019-06-09 01:58:46 さわるな変な人
@kanjizaibosatsu
さわるな変な人
@kanjizaibosatsu
@Kantaro196611 それは、「我々が共有する世界は、それを可能にする公理が成り立つものだから」と答えるよりないんじゃないかな。 中3の定期テストしょっぱなというタイミングはともあれ、そこまで考えて欲しいのなら良い問いにも思えます🤔
2019-06-09 12:08:45 さわるな変な人
@kanjizaibosatsu
さわるな変な人
@kanjizaibosatsu
@Kantaro196611 それなりな高級言語でのプログラミング言語の話であれば、かつ、「ひとつの文字で」のところを「ひとつの変数で」と読み替えれば、「変数には、評価前の式への参照を設定できるから」で済みそうですが…。
2019-06-09 12:18:44 秋晴れ
@AkibareGO
秋晴れ
@AkibareGO
@Kantaro196611 答え:分配法則が成り立つから。 別解:Mで置き換えて分配法則を使っても、(b-2)で分配法則で計算しても、同じ結果になるから 中3数学の式の展開の時に、ちゃんと先生の説明を聞いていた人ならすぐ答えられるはずです。なんだ簡単じゃんと、分配法則なんかちゃちゃっと済ましていた人は答えられない
2019-06-09 01:20:52 ジロリアン
@aglssbty
ジロリアン
@aglssbty
@Akimoto_Oka @Kantaro196611 それは(a+3)MをaM+3Mと書けることの説明であって、(a+3)(b-2)を(a+3)Mと書けることの説明になっていないですね。
2019-06-09 09:10:03 秋晴れ
@AkibareGO
秋晴れ
@AkibareGO
@aglssbty @Kantaro196611 大学数学とか、高校数学とか、理系数学とか、文系数学とか、中学数学とか、小学算数とか、なぜか日本には沢山の切り分けがあります。中学数学では、どう教えているのかですね。
2019-06-09 11:58:30 ∬
@sol_phusia
∬
@sol_phusia
@Akimoto_Oka @Kantaro196611 なんか的から反れてません???? それと最後の厭味ったらしい文はいけ好かないですね
2019-06-09 01:54:39 秋晴れ
@AkibareGO
秋晴れ
@AkibareGO
@eyzk_12 @Kantaro196611 最後のは嫌みじゃなくて変なしがらみで勉強させられてこなかった人は良かったねってことです 例 ・「3このリンゴがのったおさらが4まいあります。りんごはいくつですか」の答え「12こ」⇒×「4×3=12」⇒×「3×4=12こ」⇒〇 ・文章題で連立方程式を使うと× ・図形問題で高校の公式を使うと×
2019-06-09 12:09:56 ∬
@sol_phusia
∬
@sol_phusia
@Akimoto_Oka @Kantaro196611 今なぜ文字に置き換えられるかが論点であり、その例は全く関係ないと思うんですが なんかどんどん反れて言ってて意味がわかりません
2019-06-09 12:14:46 秋晴れ
@AkibareGO
秋晴れ
@AkibareGO
@eyzk_12 @Kantaro196611 「今なぜ文字に置き換えられるかが論点であり」←これが間違っています。そこに興味が行くのは、数学大好きさんだからです。この出題者の意図は分配法則をわかっているかだと思います。なぜなら、中学3年の数学の問題なので、しかもおそらく中3で分配法則をやっているので中高一貫校でもないでしょう
2019-06-09 12:19:55